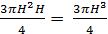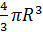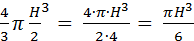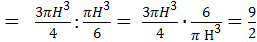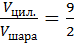Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральная симметрия параллелепипеда.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Т19.3 Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. · Точка пересечения диагоналей параллелепипеда является его центром симметрии. Прямоугольный параллелепипед. 4 Прямой параллелепипед, у которого основание является прямоугольник, называется прямоугольным параллелепипедом (все грани прямоугольники). 5 Прямоугольный параллелепипед, у которого ребра равны называется кубом. Т19.4 В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений. Симметрия прямоугольного параллелепипеда. У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии – точка пересечения его диагоналей. У него так же есть три плоскости симметрии, проходящие через центр симметрии параллельно граням. Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме названных. Если же у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии. Эта плоскость диагональных сечений. Объем призмы. Объем любой призмы равен произведению площадей ее основания на высоту. Объем любого параллелепипеда равен произведению площади основания на высоту. Объем прямоугольного параллелепипеда с линейными размерами a,b,s вычисляются по формуле
Объем наклонного параллелепипеда. Понятия объема. Тело называется простым, если его можно разбить на конечное число треугольных пирамид. Для простых тел объем – это положительная величина, численное значение которой обладает следующими свойствами: 1) Равные тела имеют равные объемы. 2) Если тело разбито на части, являющимися простыми телами, то объем этого тела равен сумме объемов его частей. Объем куба, ребро которого равно единица длины, равен единицы. Задачи: 1. Найдите объем прямой призмы
3)
4) 5)
2. Найдите объем наклонной призмы, у которой основанием является треугольник со сторонами 20, 20 и 24см, а боковое ребро, равное 16см, составляет с плоскостью основания угол 60˚.
 ма ма
АВ=20см, AC=20cм, ВС=24см, Найти Vпр.
Решение: 1) 2)По формуле Герона найдем S осн.
р- полупериметр
4)
5) Vпр.=192 Ответ: 3. Диагональ прямоугольного параллелепипеда равна 36 см и составляет угол 30°, с плоскостью боковой грани и угол в 45° с боковым ребром. Найдите объем параллелепипеда.
АС1 = 36 см
Найти: Vпарал. Решение: АС1 – наклонная к АА1В1В, АВ1 – её проекция
1) Vпарал. = abc = Sосн. · H 2) ∆ АВ1С1:
3) ∆ АА1С1: АА1 = АС1 · cos45° = 4) ∆ АА1С1:
АА1 = А1С1 = 18 5) ∆ А1В1С1: По т. Пифагора А 1В1 = 6) Vпарал. = 18 · 18· Ответ: 5832 4. В правильной призме четырёхугольной сторона основания 8 см. Диагональ призмы 18 см. Найдите объем призмы.
B1D1 = 3) По теореме Пифагора: BB1 = 4) Vпр = 64 *14 = 896 см3. Ответ: 896 см3.
Пирамида. О: Многоугольник, одна из грани которой – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамида. Отрезки соединяющих вершину пирамиды с вершинами основания, называются боковыми рёбрами. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Усеченная пирамида. Т19.5 Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду. Правильная пирамида. О: Пирамида называется правильной, если ее основание является правильный многоугольник, а основание высоты соединяет с центром этого многоугольника. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Т19.6 Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофемы. Объем пирамиды. О: Объем любой треугольной пирамиды равен одной третьей произведения площади основания на высоту: V = Задачи:
1. В правильной четырёхугольной пирамиде боковые рёбра 40см, а высота 32см. Найти объём пирамиды.
SC = 40см, SO = 32см, SO Найти: Vпр. Решение: 1) Vпр. = 2) Так как пирамида правильная четырёхугольная, значит в основании её лежит квадрат. Sкв. = 3) По теореме Пифагора: ОС = 4) SABCD = Ответ:
Так как пирамида правильная, SD – апофема. По теореме Пифагора найдём SD (катет). SD = SB2 – DB2 = Sбок. = Ответ: Sбок. =
3. Основанием пирамиды служит равнобедренный треугольник АВС, в котором АВ = ВС = 13см, АС = 10 см, каждое боковое ребро пирамиды образует с её высотой угол 30
R – радиус описанной окружности
По теореме косинусов в треугольнике АВС:
100 = 2 * 2 * 169 *
Значит, R = OB = Из треугольника SOB найдём высоту SO: SO S S V = Ответ: 9. Тела вращения.
Тела вращения.
Цилиндр. 1 В цилиндр площадь осевого сечения которого равна 48см2 вписана призма. Основанием призмы является прямоугольный треугольник с катетом равным 4
2.
АВ – диаметр, R = 3.АА1В1В – осевое сечение цилиндра. АА1В1В = АВ * АА1 48 = 8 * АА1 АА1 = 4. VЦил.= Ответ:
Запомни! (Частный случай.)
а КМ = 15м. 4) Рассмотрим треугольник О1КМ: По теореме Пифагора: О1М = 5) Sосн. = Ответ: Sосн. =
3. В шар, радиус которого равен 18см, вписан цилиндр. Диагональ осевого сечения цилиндра составляет с основанием угол 30о. Найдите площадь боковой поверхности цилиндра.
 шар (0;18), АВСD – цилиндр, шар (0;18), АВСD – цилиндр,
вписан в шар, Найти: Sбок.цил.
1) Sбок.цил.= 2 2) ∆ ADC: СD = ∆ADC: 3) AD = AC Rосн.цил = 4) Sбок.цил. = 2П Ответ: 324 П 4. Около шара, радиус которого равен 15 м, описан цилиндр. Найдите площадь боковой поверхности цилиндра.
АВСД – цилиндр, описан около шара Найти: Sбок. пов.
Решение 1) Sбок. пов. = 2πRH 2) D = 2 · ОО1 = 15 · 2 = 30м 3) Sбок. пов. = 2π · 15 · 30 = 900π м2 Ответ: 900π м2
Дано: ω сфера (О;9), АВСД – цилиндр, описан около шара Найти: Vцил Решение 1) Vцил. = π R2H 2) Н = 2R = 2 · 9 = 18 см 3) Vцил. = π · 92 · 18 = 1458 π см3 Ответ: 1458 π см3 6. Около шара описан цилиндр. Найдите площадь боковой поверхности цилиндра, если его высота равна 24см.
АВСД – цилиндр, описан около шара H = 24cм Найти: Sбок. пов. Решение 1) Sбок. пов. = 2πRH 2) R = 3) Sбок. пов. = 2π · 12 · 24 = 576 π cм2 Ответ: 576 π cм2 7. В цилиндре АВСД проведен отрезок С1Д1, равный 18 см и параллельный основанию. Известно, что радиус основания равен 40 см. Найти расстояние от отрезка С1Д1 до оси цилиндра.
С1Д1 = 18 см
 С1Д1 С1Д1
1) Рассмотрим ЕС1Д1: ЕС1 = ЕД1 = 40см, как радиусы одной окружности по Т 20.1 2) ЕК КД1 = 9 см 3) ∆ ЕКД1: По т. Пифагора ЕК = Ответ: 7
Конус. О: Тело, полученное при вращении прямоугольного треугольника вокруг его катета, называется конусом.
Развёртка: Sбок. =
Задачи:
 . Грань пирамиды, проходящая через данный катет составляет с основанием угол . Грань пирамиды, проходящая через данный катет составляет с основанием угол 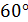 . Найдите объём конуса. . Найдите объём конуса.
R = 3. Рассмотрим
a) SK b) OK На основании Т17.2 заключаем, что плоскость SKD 4. ОК – средняя линия треугольника АСВ, значит ОК = 5. ВС = АС * 6. OK = 7. SO = OK * 8. Vкон. = Ответ: Vкон. =
Составляем пропорцию: 3. Пусть SO = x, тогда SE = x – 10 4. ED =
5. 10х = 15(х-10) 10х = 15х – 150 10х – 15х = -150 -5х = -150 |: (-5) х = 30 Ответ: 30см.
Дано: SAB-конус
SB =30см AB =36см
Решение: 1. S шара = 4π 2. ∆SAB – осевое сечение конуса, равнобедренный w – окружность, вписанная в ∆ SAB r =
P = a + b + c 3. Sравноб. ∆ = = 4. r = 5. S шара = 4π · Ответ: 324 π
Шар. Задачи:
По теореме Пифагора: ВВ1 = 3) ∆ В1 А1 Д1:
4) 5) Sбок. парал. = (8+12) · 2 ·24 = 20 · 2 · 24 = 40 · 24 = 960 Ответ: 960
2. Дан шар. Секущая плоскость наклонена к диаметру под углом 60°, расстояние от центра шара до секущей плоскости равно
ОО¹ =
Решение: 1) Sсеч. = π 2) Рассмотрим ∆OO¹A:
По Т. о секущей плоскости шара CO¹ ┴ α O¹A = OO¹ · 3) Sсеч = π Ответ:
Цилиндр - ABCD
Найти: Решение: 1) Vцил. = π 2) Рассмотрим ∆CDA ∟СDA = 90° AD = CD · ctg30° = H 3. R осн.цил. = 4. V цил. = π 5. V шара = 6. Rшара = 7. V шара = 8. V цил. Ответ:
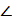 SBO = 30° SBO = 30°
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.46.174 (0.017 с.) |

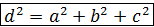
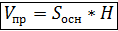
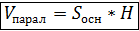
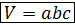
 , если угол ВАС равен 120˚, АВ=10 см, АС=6см и наибольшая из площадей боковых граней равна 105
, если угол ВАС равен 120˚, АВ=10 см, АС=6см и наибольшая из площадей боковых граней равна 105  .
.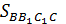 = 105
= 105  Найти: Vпр.?
Решение:
1)
Найти: Vпр.?
Решение:
1) 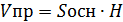 2)
2) 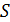 осн =
осн = 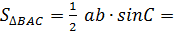 =
= 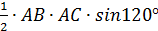 =
=
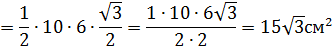
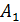
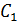
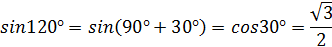
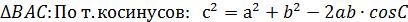
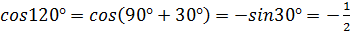
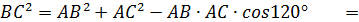
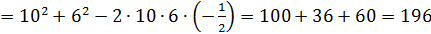 , значит ВС = 14 см.
, значит ВС = 14 см. - прямоугольник 105 =14
- прямоугольник 105 =14 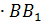 ;
; 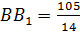
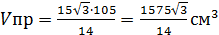
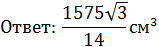
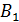
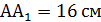
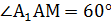
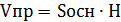
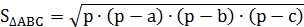

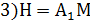
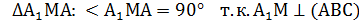
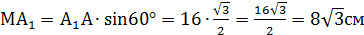
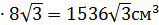
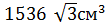
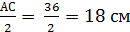 по свойству катета, лежащего напротив угла 30° в прямоугольном треугольнике.
по свойству катета, лежащего напротив угла 30° в прямоугольном треугольнике.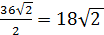 см
см АА1С1 = 90°,
АА1С1 = 90°, 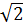 см.
см.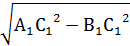 =
= 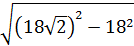 =
= 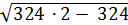 =
= 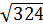 = 18 см
= 18 см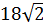 = 5832
= 5832  B1A1D1:
B1A1D1: 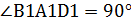 .
Так как призма правильная, значит в основании ее лежит квадрат.
По теореме Пифагора:
.
Так как призма правильная, значит в основании ее лежит квадрат.
По теореме Пифагора:
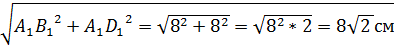
 A1B1C1 D1
A1B1C1 D1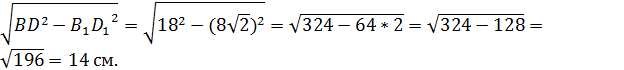
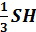 .
.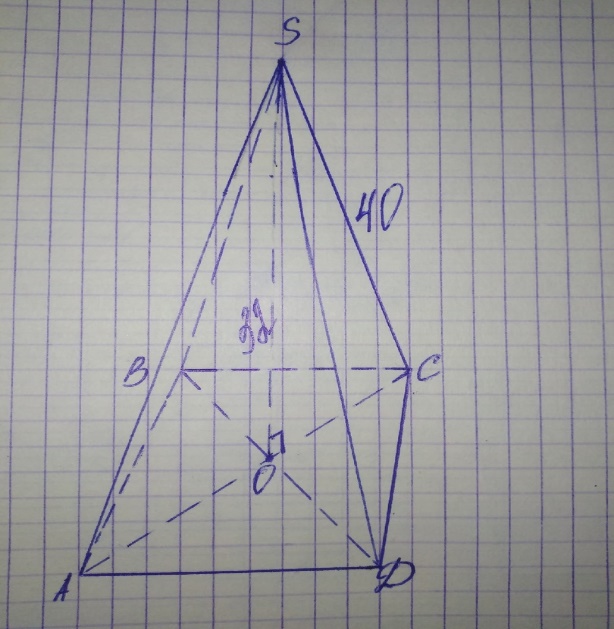 Дано: SABCD – правильный четырёхугольник,
Дано: SABCD – правильный четырёхугольник, Sосн. * Н
Sосн. * Н
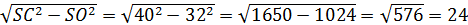 см, значит АС = 48см, BD = 48см.
см, значит АС = 48см, BD = 48см.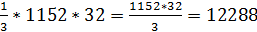 см3.
см3.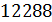 см3.
см3. Р осн. * Н бок.
2) О – центр основания пирамиды. Точка пересечения медиан треугольника АВС – точка О.
3)
Р осн. * Н бок.
2) О – центр основания пирамиды. Точка пересечения медиан треугольника АВС – точка О.
3) 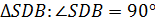
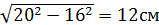
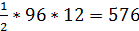 см2
см2 см2
см2
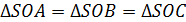 , они имеют равный острый угол, тогда ОВ = ОС = ОА =R, где
, они имеют равный острый угол, тогда ОВ = ОС = ОА =R, где
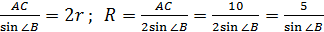
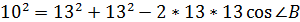
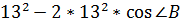
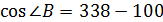
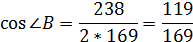

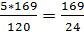
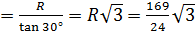
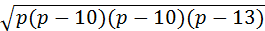 , где p =
, где p = 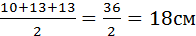
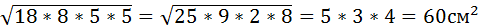
 S
S 
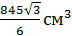
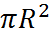 VШара =
VШара = 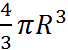
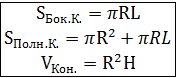
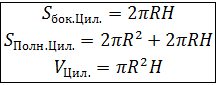
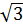 и прилежащим к нему углом 30
и прилежащим к нему углом 30 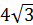

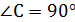 ,
, 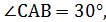 АС = 4
АС = 4 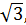 SAA1B1B = 48см2
Найти: VЦил.
Решение:
1. VЦил.=
SAA1B1B = 48см2
Найти: VЦил.
Решение:
1. VЦил.= 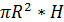
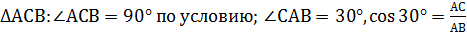
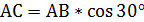
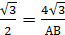 АВ =
АВ = 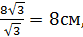 центр описанный около прямоугольного треугольника окружности лежит на середине гипотенузы, а значит
центр описанный около прямоугольного треугольника окружности лежит на середине гипотенузы, а значит = 4см.
= 4см.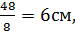 значит Н = 6см.
значит Н = 6см.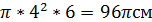 3
3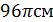 3
3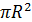 2)
2)  , значит О1К – медиана треугольника MO1Q.
MQ = 30, так как сечение MNPQ, если квадрат,
, значит О1К – медиана треугольника MO1Q.
MQ = 30, так как сечение MNPQ, если квадрат,
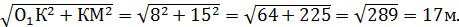
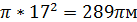 2
2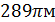 2.
2.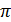 RH
RH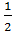 AC =
AC = 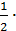 36 = 18cм по свойству катета, лежащего напротив угла в 30 в прямоугольном треугольнике, а значит H =1 8см
36 = 18cм по свойству катета, лежащего напротив угла в 30 в прямоугольном треугольнике, а значит H =1 8см cos30o =
cos30o = 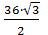 =18
=18 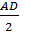 =
= 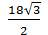 = 9
= 9 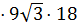 = 324 П
= 324 П  см2
см2 см2
см2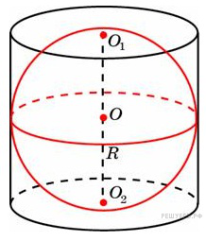 Дано: ω шар (О;15),
Дано: ω шар (О;15),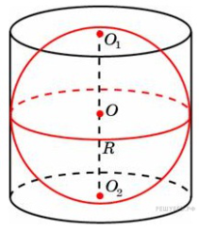 5. Найдите объем цилиндра, описанного около сферы радиуса 9см.
5. Найдите объем цилиндра, описанного около сферы радиуса 9см. =
= 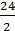 = 12 cм
= 12 cм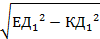 =
= 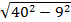 =
= 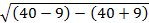 =
= 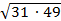 = 7
= 7 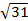 см
см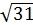 см
см

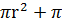 rl
VКон.=
rl
VКон.= 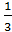 r2 * H
r2 * H
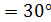
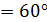 Найти: Vкон.
Решение:
1. Vкон. =
Найти: Vкон.
Решение:
1. Vкон. = 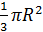 2.
2. 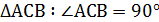 по условию
АВ = 14м по свойству катета лежащего против угла в 30
по условию
АВ = 14м по свойству катета лежащего против угла в 30 
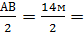 7m.
7m.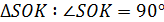 , так как SO высота конуса и пирамиды.
, так как SO высота конуса и пирамиды.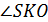 – линейный угол двугранного угла ребром АС и гранями SAC и ACВ, так как
– линейный угол двугранного угла ребром АС и гранями SAC и ACВ, так как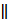 BC.
BC.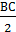 .
.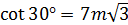 .
.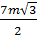 .
.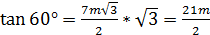 .
.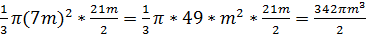 .
.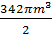
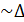 SED: оба прямоугольные и
SED: оба прямоугольные и
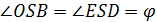 .
2. Из подобия треугольников следует пропорциональность сходства их сторон.
.
2. Из подобия треугольников следует пропорциональность сходства их сторон.
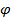
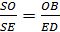
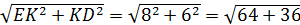 =
= 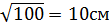 .
.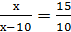
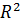
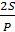
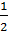 a
a 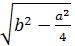 =
= 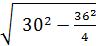 =
= 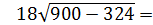
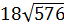 = 18 · 24 = 432
= 18 · 24 = 432 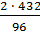 = 9см, а значит R шара = 9см
= 9см, а значит R шара = 9см = 4π · 81 = 324 π
= 4π · 81 = 324 π 
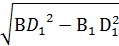
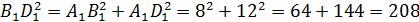
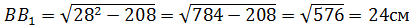 , а значит H = 24см
, а значит H = 24см . Найти площадь сечения.
. Найти площадь сечения.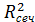
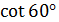 =
= 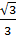 =
= 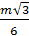 , значит Rсеч =
, значит Rсеч = 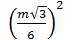 =
= 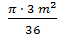 =
= 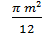
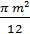 .
.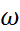
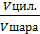
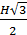
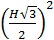 · H =
· H =