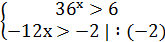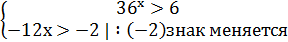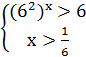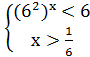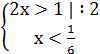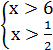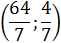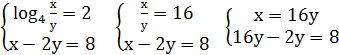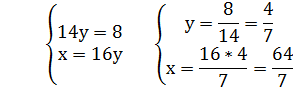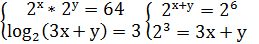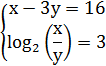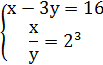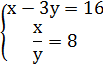Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы сокращенного умножения.
Свойства степеней (m, n – целые числа).
Примеры решения: 1. 2) 3) 4) Ответ: 2.81432732∙16433253=34343325∙24342535=3412∙2412336∙2515=33∙2332∙23=27∙89∙8=3 Ответ:3 3. 2734∙2732335∙337=3343∙3313335+7=3312∙3363312=34∙32234=3634=36-4=32=9 Ответ: 9 4. 221∙821732∙734=221∙2312736=2∙12∙23272=2272=449 Ответ:449
1. 2. 3. 4. 5. (( 6.
5. Тригонометрия.
Тригонометрия часть I. 1. Упростить:
= Ответ:
2. Докажите тождество
Приведём левую часть к правой
Тождество доказано.
Экзаменационные задания. 3. Доказать тождество Приведём левую часть к правой
Тождество доказано.
4. Упростить:
= Ответ:
5. Найдите значение выражения при х=
При х =
Ответ:
Тригонометрия I часть. Экзаменационные задания.
Тригонометрия часть II. Уравнения.
2 Введение новой переменной. Сведение к квадратному.
a = 2, b = - 7, c = 3
E( Ответ: 4 Вынесение общего множителя за скобки. Ответ:
Однородное тригонометрическое уравнение.
1. Уравнения, в левой части которого каждое слагаемое имеет одинаковую степень, а в правой части нуль, называется однородным. 2. Степень произведения определяется как сумма степеней множителей. Например: 3. Такое уравнение решаем путём деления обеих частей на 4. Но прежде чем решить, нужно посмотреть, а можно ли решить? 5. Ошибка чаще всего встречается при решении неполного однородного уравнения. Пример:
Уравнение II степени. Если мы будем делить обе части на Решаем путем вынесения общего множителя за скобку.
Когда уравнение равно нулю? Когда хотя бы один из множителей равен нулю.
Уравнение однородное I степени. Будем делить обе части на Рассуждаем так: 1. Допустим 2. 3. 4.
Ответ:
1. Упростить
Ответ:
2. Упростить:
Замечания: 1. 2. 3. Ответ: 3. Упростить:
Замечания: 1. 2. 3.
4. Упростить.
5. Докажите тождество.
Тождество доказано. 6. Докажите тождество 5- Приведем левую часть к правой 5 Тождество доказано
7. Докажите тождество.
Приведем левую часть к правой
Тождество доказано.
8. Упростить:
Замечания: 1) 2) 3) 4) Ответ: 1
9. Упростить:
Ответ:
6. Системы нелинейных уравнений.
1. 1)Выясним при каких значениях в числители и знаменатели дроби равны нулю, и решим методом интервалов. 2)
Y = Y(1) = Y(0) = 2 Способ: 1. Дробь 2. Рассмотрим два случая:
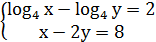
3.
2х = 2 у = 6 - х х = 1 у = 5
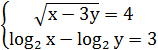 
8у – 3у = 16 5у = 16 у = х =
7. Интеграл.
Определённый интеграл. Формула Ньютона – Лейбница. О: Интегралом от a до b f(x)dx называется приращение первообразной.
Формула Ньютона – Лейбница. a – нижний предел интегрирования. b – верхний придел интегрирования.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 2597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.120.133 (0.057 с.) |

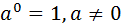
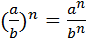 , b
, b 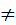 0
0
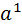 =a
=a 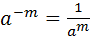 , a
, a 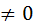

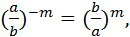 a
a 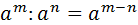 , a
, a 






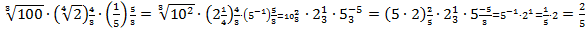
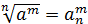

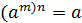 mn
mn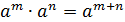

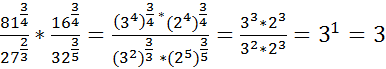
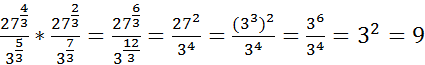
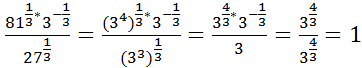

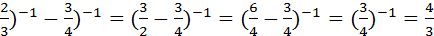
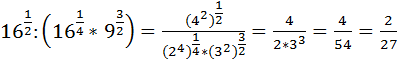
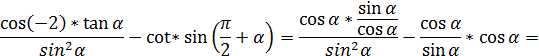
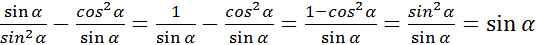
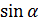 .
.
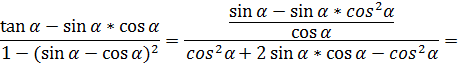

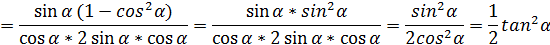
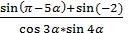 =
= 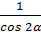

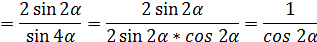
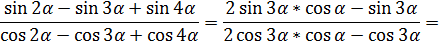

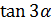

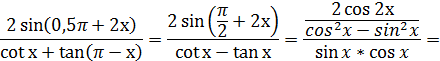
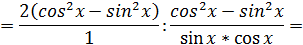
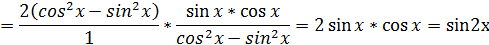
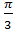 имеем:
имеем:
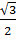

 I.
I. 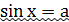
 II.
II. 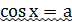
 III.
III. 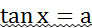 .
.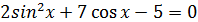
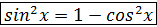
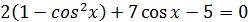
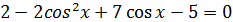

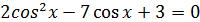


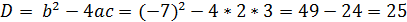
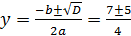
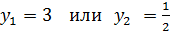

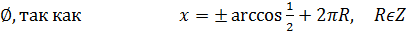
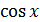 )
) 
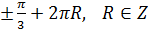
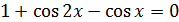
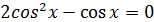

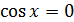 или
или 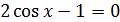
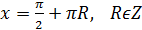
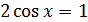
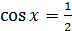
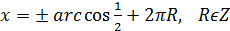


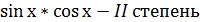 .
.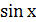 или
или  в степени, равной степени однородности уравнения.
в степени, равной степени однородности уравнения.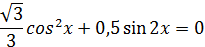

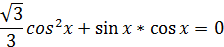
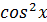 , то мы должны рассуждать так. Допустим
, то мы должны рассуждать так. Допустим 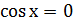 , тогда
, тогда 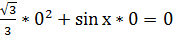 . Тогда
. Тогда 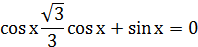
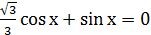

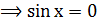 , а одновременно этого не может быть.
, а одновременно этого не может быть.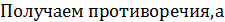 а оно возникло в результате неверного предположения.
а оно возникло в результате неверного предположения. и делить на него можно.
и делить на него можно.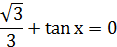
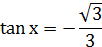
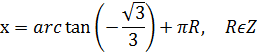
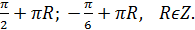
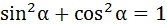 2.
2.  =1-
=1- 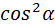 3.
3. 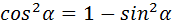 4. tg
4. tg 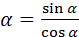 5. ctg
5. ctg 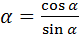 6. tg
6. tg 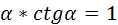 7. 1+
7. 1+ 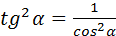 8. 1+
8. 1+ 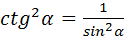
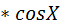 2. cos2X =
2. cos2X = 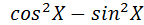 3. cos2X = 1-2
3. cos2X = 1-2  1. 4. cos2X = 2
1. 4. cos2X = 2 
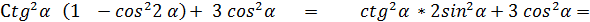
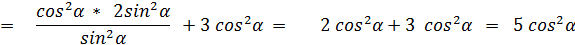
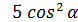
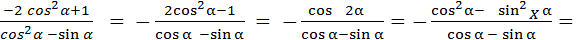
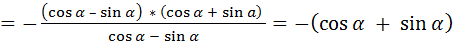 .
.
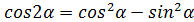
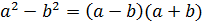
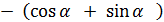
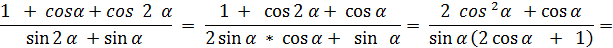
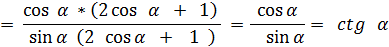

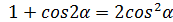 (пониж. степени №4)
(пониж. степени №4)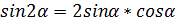 (кратн. арг. №1)
(кратн. арг. №1)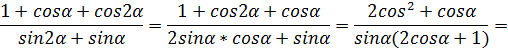
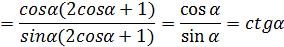
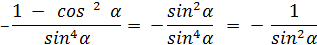
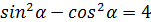
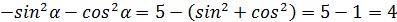
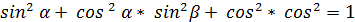

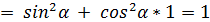
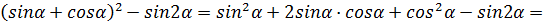

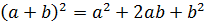
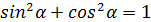
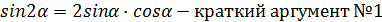
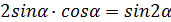
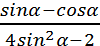 =
= 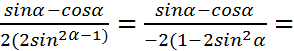

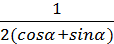
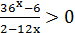
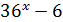 3) 2-12x = 0
3) 2-12x = 0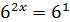 2 = 12x
2 = 12x
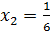

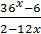
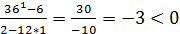
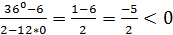
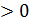 , когда числитель и знаменатель имеют одинаковые знаки.
, когда числитель и знаменатель имеют одинаковые знаки.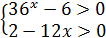 или
или