
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность и потенциал поля, создаваемого распределенными зарядами.Содержание книги
Поиск на нашем сайте
Если заряд равномерно распределен вдоль линии с линейной плотностью τ, то на линии выделяется малый участок длиной dl с зарядом
где Используя принцип суперпозиции электрических полей, интегрированием находят напряженность
Интегрирование ведется вдоль всей длины L заряженной линии. Интегрирование приводитк следующей формуледля напряженности поля, создаваемого прямой бесконечной равномерно заряженной линией или бесконечно длинным цилиндром:
где r – расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля; τ – линейная плотность заряда, τ = q / l.
При расчетах электростатического поля системы зарядов используется теорема Остроградского–Гаусса. Определение теоремы Остроградского–Гаусса для поля в вакууме: поток Математическая формула теоремы имеет следующий вид:
где Если поверхность не охватывает заряд, то поток через такую поверхность равен нулю. Значение потока вектора Е через замкнутую поверхность не зависит ни от размеров, ни от формы поверхности. Поэтому при расчетах следует выбирать поверхность такой формы, которая позволяет наиболее просто вычислить поток. Применение теоремы Остроградского–Гаусса к расчету поля приводит к следующим формулам для напряженностей и потенциалов: напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы: – при r < R E = 0; – при r = R – при r > R где q – заряд сферы. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, определяется как
Связь потенциала с напряженностью: – в общем случае – если поле однородное, то
– если поле обладает центральной или осевой симметрией, то
Работа по перемещению заряда q в электростатическом поле. При заданной напряженности поля Е работа по перемещению электрического заряда q определяется следующей формулой:
где E – напряженность поля; dl – элемент траектории L. Работапо перемещению тела с зарядом q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2 вычисляется по формуле
Эта работа идет на изменение кинетической энергии тела
где m – масса тела; υ 1 и υ 2 – начальная и конечная скорости тела.
Электроемкость – это физическая величина, численно равная заряду q, который необходимо сообщить проводнику (системе проводников), чтобы увеличить потенциал φ на 1 вольт. Формулы электроемкостей: – уединенного проводника
– двух проводников
где U – разность потенциалов проводников.
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.185.58 (0.007 с.) |

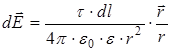 ;
; 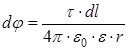 ,
,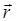 – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.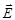 и потенциал φ поля, создаваемого распределенным зарядом:
и потенциал φ поля, создаваемого распределенным зарядом: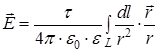 ;
; 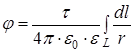 .
.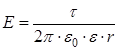 ,
,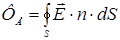 вектора напряженности Е электростатического поля через любую замкнутую поверхность S равен алгебраической сумме зарядов
вектора напряженности Е электростатического поля через любую замкнутую поверхность S равен алгебраической сумме зарядов 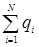 , которые охватываются этой поверхностью, деленной на электрическую постоянную.
, которые охватываются этой поверхностью, деленной на электрическую постоянную.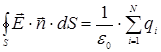 ,
,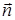 – единичный вектор нормали к элементу поверхности dS.
– единичный вектор нормали к элементу поверхности dS.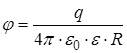 ;
;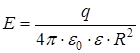 ;
; 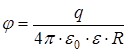 ;
;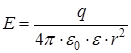 ;
; 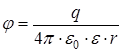 ,
,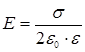 .
.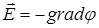 или
или 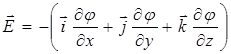 ;
;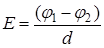 ;
; 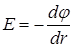 .
.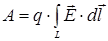 ,
,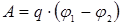 .
.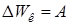 . Поэтому справедливо следующее соотношение:
. Поэтому справедливо следующее соотношение: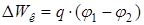 или
или 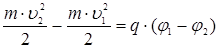 ,
,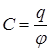 ,
,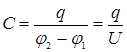 ,
,


