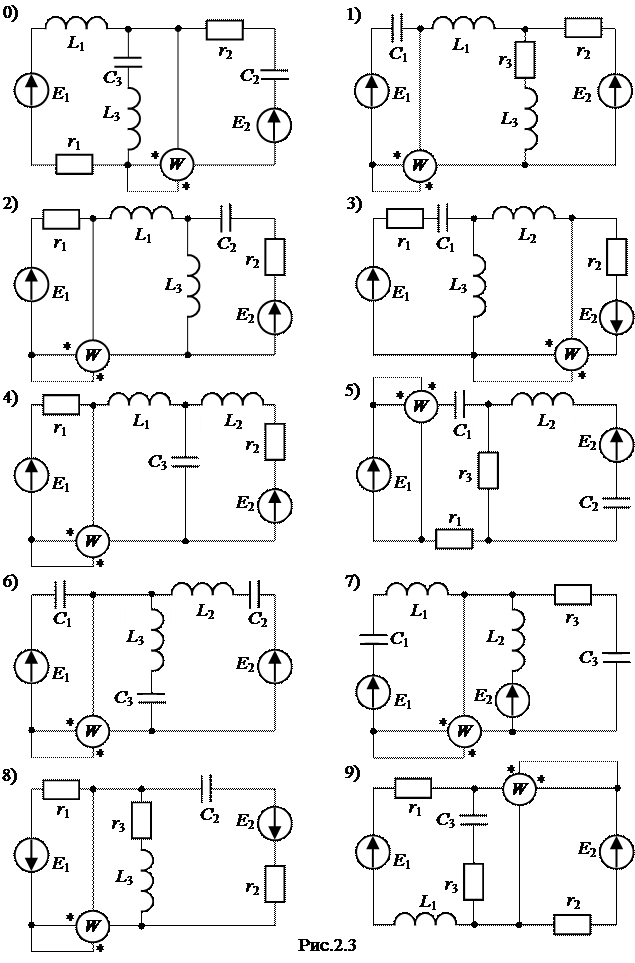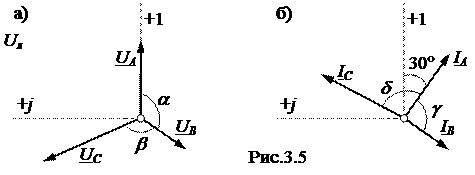Электрические цепи синусоидального тока, включая цепи со взаимной индуктивностью и четырехполюсники

 

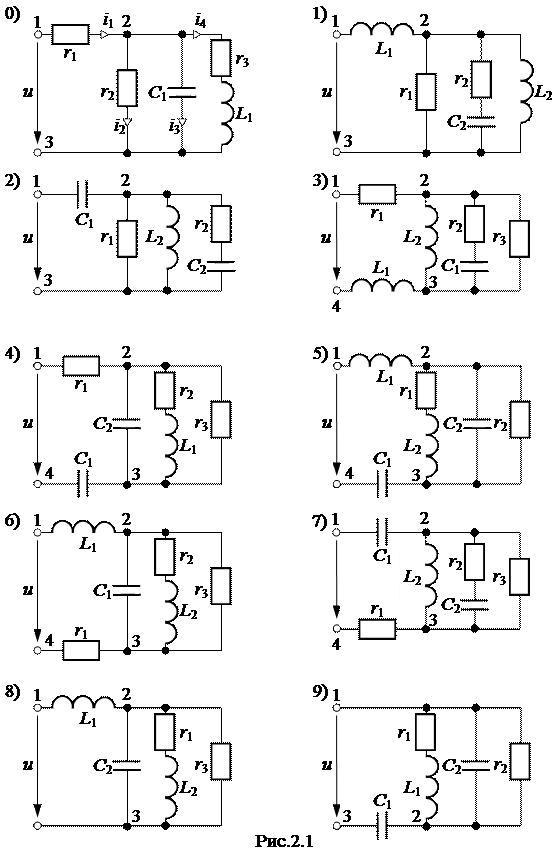
ЗАДАЧА 2.1. В схеме рис.2.1 заданы напряжение или ток в одной из ветвей (или входное напряжение) и параметры цепи (см. таблицу вариантов). Необходимо выполнить следующее:

1) рассчитать действующие значения токов во всех ветвях и напряжений на всех участках цепи (включая входное напряжение);

2) определить активную, реактивную и полную мощности цепи, а также коэффициент мощности всей цепи;

3) качественно построить векторную диаграмму напряжений, совмещенную с диаграммой токов.

Задачу решить методом проводимостей.

Таблица вариантов к задаче 2.1

Первая цифра варианта	Заданное напряжение или ток (В, А)	r 1, Ом	L 1, мГн	C 1, мкФ	r 2, Ом	L 2, мГн	C 2, мкФ	r 3, Ом
0	u =100 sin (314 t +30°)	4	12	400	10	25	200	8
1	i 1=2 sin (314 t -30°)	3	10	500	12	26	150	6
2	i 2=3 sin (314 t +15°)	5	14	300	16	27	180	10
3	u 23=50 sin (314 t +60°)	3	11	350	18	28	170	6
4	i 3=2 sin (314 t -60°)	4	16	450	10	29	160	8
5	u =200 sin (314 t +45°)	5	18	480	12	30	150	10
6	i 4=4 sin (314 t -45°)	5	20	300	14	31	100	6
7	u 23=75 sin (314 t -15°)	4	22	380	16	32	120	8
8	u =120 sin (314 t +20°)	3	24	420	18	33	140	4
9	u 23=80 sin 314 t	3	15	460	20	34	160	5

Примечание: не следует учитывать параметры элементов, отсутствующих в схеме Вашего варианта.

 

ЗАДАЧА 2.2. В схеме рис.2.2 комплексным методом:

1) рассчитать действующие значения токов во всех ветвях и напряжений на всех участках цепи (включая входное напряжение);

2) определить активную, реактивную и полную мощности цепи, а также коэффициент мощности всей цепи;

3) записать мгновенное значение любой из не заданных величин токов или напряжений;

4) рассчитать и построить топографическую диаграмму для всей цепи, совмещенную с диаграммой токов.

Таблица вариантов к задаче 2.2

Первая цифра варианта	Заданное напряжение или ток (В, А)	r 1, Ом	L 1, мГн	C 1, мкФ	r 2, Ом	L 2, мГн	C 2, мкФ	r 3, Ом	L 3, мГн	C 3, мкФ
0	u =100 sin (314 t +30°)	4	12	400	10	25	200	8	32	200
1	i 1=2 sin (314 t -30°)	3	10	500	12	26	150	6	34	280
2	i 2=3 sin (314 t +15°)	5	14	300	16	27	180	10	36	260
3	u 23=50 sin (314 t +60°)	3	11	350	18	28	170	6	26	300
4	i 3=2 sin (314 t -60°)	4	16	450	10	29	160	8	50	280
5	u =200 sin (314 t +45°)	5	18	480	12	30	150	10	30	280
6	i 2=4 sin (314 t -45°)	5	20	300	14	31	100	6	26	300
7	i 3=5 sin (314 t -15°)	4	22	380	16	32	120	8	18	275
8	u =120 sin (314 t +20°)	3	24	420	18	33	140	4	28	200
9	u 23=80 sin 314 t	3	15	460	20	34	160	5	30	240

Примечание: не следует учитывать параметры элементов, отсутствующих в схеме Вашего варианта; номера токов рекомендуется выбирать совпадающими с с номерами ветвей.

 

ЗАДАЧА 2.3. В схеме рис.2.3 заданыт параметры цепи и ЭДС источников. Известно также, что ЭДС Е ₁  опережает ЭДС Е ₂  на угол   a.

Необходимо:

1) по законам Кирхгофа составить систему уравнений для определения токов во всех ветвях цепи (систему уравнений решать не следует);

2) определить комплексы токов во всех ветвях цепи методом контурных токов;

3) составить баланс активных и реактивных мощностей;

4) определить показание ваттметра;

5) построить топографическую диаграмму, совмещенную с векторной диаграммой токов;

6) проверить величины всех токов методом узлового напряжения.

Таблица вариантов к задаче 2.3

I-я цифра варианта	E 1, B	E 2, B	a, град	r 1, Ом	L 1, МГн	С 1, мкФ	r 2, Ом	L 2, мГн	С 2, мкФ	r 3, Ом	L 3, мГн	С 3, мкФ	f, Гц
0	100	100	60	4	20	200	5	60	250	4	10	200	50
1	100	120	45	6	30	200	4	50	300	6	20	300	60
2	220	140	30	6	40	300	8	10	200	8	30	200	50
3	200	200	90	8	4	140	8	20	180	10	40	160	100
4	200	220	60	10	6	190	12	8	140	4	50	120	50
5	200	240	30	12	8	200	14	10	100	8	50	150	60
6	240	280	45	20	10	50	24	12	120	6	8	110	50
7	280	240	60	40	4	200	30	14	140	10	10	120	100
8	400	100	90	3	30	300	10	16	200	4	12	300	50
9	50	50	15	40	10	100	20	30	200	6	14	200	60

Примечание: учтите параметры только тех элементов, которые имеются в Вашей схеме.

 

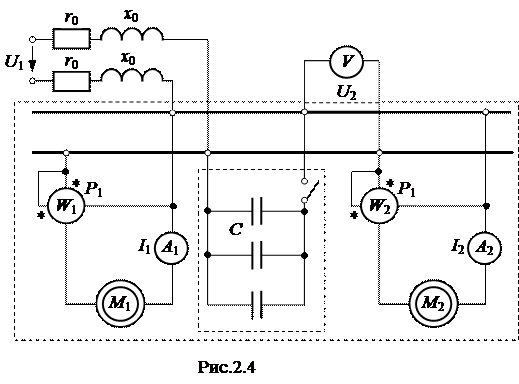
ЗАДАЧА 2.4. Два электродвигателя переменного тока подключены параллельно к сети с напряжением U ₂ и работают с низким коэффициентом мощности. Измерительные приборы в цепи каждого электродвигателя показывают токи I ₁ и I ₂, а также мощности Р ₁ и Р ₂  (рис.2.4).

Каждый провод линии электропередачи, питающей оба электродвигателя, имеет активное сопротивление r ₀ и индуктивное   x ₀.  Коэффициент мощности данной установки может быть повышен включением параллельно двигателям батареи конденсаторов. Числовые значения всех величин, необходимых для расчета, приведены в таблице вариантов.

Необходимо:

1. Изобразить расчетную схему.

2. Рассчитать заданную электрическую цепь до подключения конденсаторов и определить:

а) ток в линии;

б) напряжение в начале линии;

в) потерю и падение напряжения в линии;

г) активную, реактивную и полную мощности в конце линии и мощность потерь в проводах;

д) коэффициент мощности установки;

е) КПД линии.

3. Рассчитать компенсационную установку для полученния       cos j _к = 0.95 (j _к > 0) и определить для указанного значения коэффициента мощности емкость и мощность батареи конденсаторов.

4. Выполнить расчет цепи в режиме компенсации (конденсаторы включены) и найти все величины, которые были найдены до включения конденсаторов.

Полученные результаты свести в таблицу и сравнить для различных режимов работы электродвигателей (до компенсации и с соs j _к = 0.95).  Отме-тить, какие выгоды дает повышение коэффициента мощности установки.

Таблица для сравнения результатов расчета

Режим работы	Без конденсаторов	С конденсаторами
Коэффициент мощности в конце линии
Ёмкость батареи конденсаторов, мкФ
Мощность батареи конденсаторов, квар
Ток в линии, А
Напряжение в начале линии, В
Потеря напряжения в линии, В
Падение напряжения в линии, В
Активная мощность в начале линии, кВт
Мощность потерь в линии, кВт
КПД линии, %
Реактивная мощность в конце линии, квар

Указания:

1. При всех расчетах напряжение в конце линии   U ₂ и мощности двигателей Р ₁ и   Р ₂ считать неизменными (рекомендуется обозначать   Р ₁+ Р ₂= Р_н).

2. Частоту тока принять равной промышленной частоте f = 50 Гц.

3. Решать задачу рекомендуется комплексным методом.

Таблица вариантов к задаче 2.4

Первая цифра варианта	r 0, Ом	x 0, Ом	Втораяя цифра варианта	I 1, A	I 2, A	P 1, кВт	Р 2, кВт	U 2, B
0	0.03	0.04	0	60	100	5	8	127
1	0.02	0.03	1	70	90	12	14	220
2	0.04	0.06	2	80	75	16	15	380
3	0.06	0.04	3	90	70	40	32	660
4	0.05	0.06	4	100	80	60	50	1140
5	0.06	0.05	5	95	85	7	6	127
6	0.03	0.05	6	85	95	14	12	220
7	0.04	0.05	7	75	85	15	18	380
8	0.05	0.06	8	65	80	30	35	660
9	0.05	0.03	9	82	65	60	40	1140

 

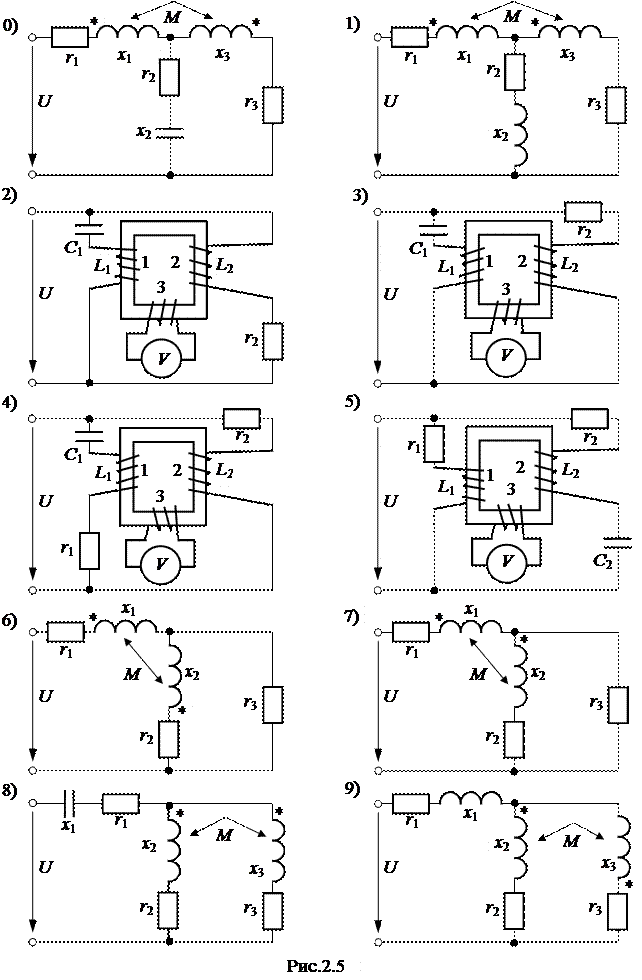
ЗАДАЧА 2.5. На рис. 2.5 изображена схема электрической цепи, содержащая индуктивно связанные обмотки (третья обмотка в схемах 2-3-4-5 замкнута на вольтметр с очень большим сопротивлением, током которого можно пренебречь).

Напряжение сети и параметры схем приведены в таблице вариантов.

Необходимо выполнить следующее:

1) составить уравнения по законам Кирхгофа для определения действующих значений токов во всех ветвях;

2) устранить ("развязать") индуктивную связь между обмотками, вычертив эквивалентную схему и определив ее параметры;

3) пользуясь любой схемой (исходной или эквивалентной), рассчитать действующие значения токов во всех ветвях;

4) определить показание вольтметра (в схемах 2-3-4-5);

5) рассчитать активную мощность взаимоиндукции, передаваемую через магнитное поле из одной обмотки в другую, и направление ее передачи;

6) для исходной схемы построить векторную или топографическую диаграмму, совмещенную с диаграммой токов.

Таблица вариантов к задаче 2.5 (схемы 2-3-4-5)

1-я цифра варианта	U, B	r 1, Ом	w L 1, Ом	1/ w C 1, Ом	r 2, Ом	w L 2, Ом	1/ w C 2, Ом	w М 12, Ом	w М 13, Ом	w М 23, Ом
0	127	10	20	10	20	10	20	14	18	20
1	220	20	12	40	24	20	10	8	6	8
2	380	24	30	20	20	20	30	24	20	25
3	660	36	30	20	20	30	40	20	25	24
4	1140	36	20	30	30	20	40	30	12	12
5	127	12	20	12	10	12	20	12	12	18
6	220	18	20	24	10	15	20	14	12	16
7	380	24	24	30	15	30	20	20	15	20
8	660	36	30	20	20	30	40	24	20	25
9	1140	24	40	20	30	40	30	30	20	30

 

Таблица вариантов к задаче 2.5 (схемы 0-1-6-7-8-9)

1-я цифра варианта	U, B	r 1, Ом	x 1, Ом	r 2, Ом	x 2, Ом	r 3, Ом	x 3, Ом	w М, Ом
0	220	5	10	10	15	12	12	10
1	380	8	12	12	18	18	12	10
2	660	10	14	20	24	24	16	12
3	127	3	6	10	16	15	20	6
4	1140	12	10	22	26	26	18	14
5	127	4	8	10	14	15	12	8
6	220	6	10	12	18	18	20	8
7	380	8	16	15	20	20	18	10
8	660	14	15	25	20	30	18	15
9	1140	22	18	15	30	16	40	25

Примечание: не следует учитывать параметры элементов, отсутствующих в схеме Вашего варианта.

 

ЗАДАЧА 2.6. Определить коэффициенты четырехполюсника рис.2.6 в формах   А, Н и Z  и рассчитать его характеристические параметры. Вычертить Т- или П-образную схему замещения четырехполюсника и рассчитать ее параметры. Числовые значения параметров схемы четырехполюсника заданы в таблице вариантов.

Таблица вариантов к задаче 2.6

1-я цифра варианта	0	1	2	3	4	5	6	7	8	9
r, Ом	30	10	50	40	50	30	60	40	80	20
xL, Ом	10	60	40	60	50	50	70	30	100	50
xC, Ом	80	10	30	90	20	10	30	80	40	60
Схема замещ.	П	Т	П	Т	П	Т	П	Т	П	Т

 

3. ТРЕХФАЗНЫЕ ЦЕПИ

 

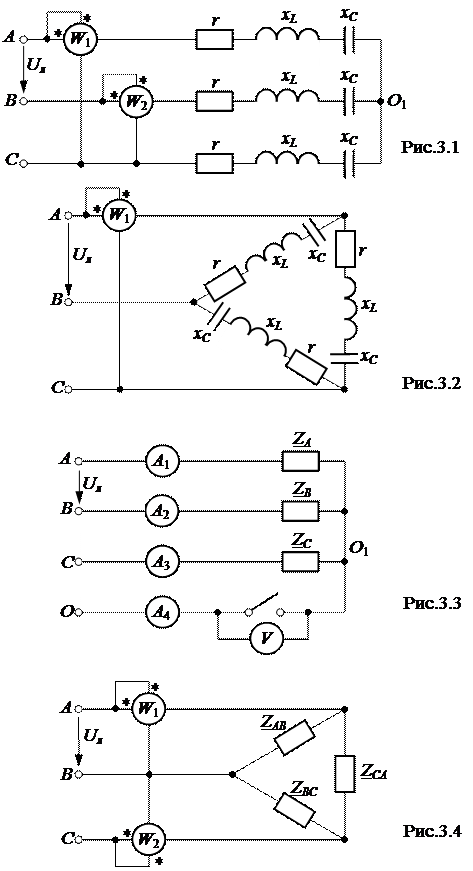
ЗАДАЧА 3.1. Три одинаковых приемника энергии с сопротивлениями r, x_L и x_C каждый подключены к трехфазному генератору с линейным напряжением U _л. По заданным в таблице вариантов параметрам схемы определить фазные и линейные токи и напряжения, а также показания ваттметров для следующих случаев:

1) приемник соединен звездой (рис. 3.1) и

а) нагрузка фаз симметрична;

б) одна фаза приемника оборвана (см. табл.);

в) один приемник закорочен (см. табл.);

г) сделать вывод о влиянии обрыва провода или короткого замыкания фазы приёмника на величины токов и напряжений по сравнению с симметричным режимом;

2) приемник соединен треугольником (рис. 3.2) и

а) нагрузка фаз симметрична;

б) один линейный провод оборван (см. табл.);

в) одна фаза приемника разомкнута (см. табл.).

Для каждого случая вычертить схему и построить векторную диаграмму напряжений и токов. Сравнить активные мощности симметричного трёхфазного приемника, соединенного по схеме звезды и по схеме треугольника и питающегося от одного и того же источника.

Таблица вариантов к задаче 3.1

1-я цифра варианта	0	1	2	3	4	5	6	7	8	9
U л, В	220	380	660	1140	127	127	220	380	660	1140
2-я цифра варианта	0	1	2	3	4	5	6	7	8	9
r, Ом	3	4	0	0	8	6	16	16	12	12
xL, Ом	4	0	10	20	6	8	12	0	16	0
xC, Ом	0	3	20	10	0	0	0	12	0	16
Для звезды: оборвана фаза закорочена фаза	А В	В С	С А	С В	В С	А С	А В	В А	С А	В В
Для треугольника: оборван линейный провод оборвана фаза	С АX	B CZ	A BY	C BY	B AX	A CZ	C CZ	B CZ	A AX	C BY

 

ЗАДАЧА 3.2. Три приемника с сопротивлениями Z _A, Z _B, Z _C соединены звездой и подключены к симметричному трехфазному генератору (рис. 3.3) с линейным напряжением U_л.

Определить показания приборов, активную мощность, потребляемую приемниками, и построить векторные диаграммы для двух случаев:

    а) нулевой провод включен;

б) нулевой провод выключен.

Параметры элементов схемы заданы в таблице вариантов.

Таблица вариантов к задаче 3.2

Первая цифра варианта	0	1	2	3	4	5	6	7	8	9
U л, В	1140	660	380	220	127	1140	660	380	220	127
Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
Z A, Ом	- j 10	8+ j 6	20	6+ j 8	3+ j 4	10	20	- j 16	- j 10	10
Z B, Ом	4+ j 3	- j 16	6+ j 8	10	- j 10	8+ j 6	- j 16	6+ j 8	13	- j 13
Z C, Ом	10	20	- j 10	3- j 4	5	- j 10	8+ j 6	20	12+ j 5	5+ j 12

 

ЗАДАЧА 3.3. Трехфазный приемник, соединенный треугольником, питается от симметричного генератора с фазным напряжением U_ф (рис. 3.4). Сопротивления фаз приемника Z _AB, Z _BC, Z _CA  и напряжение U_ф заданы в таблице вариантов. Определить все токи, показания приборов и построить векторную диаграмму напряжений и токов.

Таблица вариантов к задаче 3.3

Первая цифра варианта	0	1	2	3	4	5	6	7	8	9
U ф, В	660	380	220	127	380	660	380	220	127	220
Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
Z AB, Ом	6+ j 8	8- j 6	20	3+ j 4	25	5- j 12	- j 20	40	16- j 12	- j 10
Z BC, Ом	10- j 10	10	5- j 12	8	5+ j 12	10	5+ j 12	12- j 16	15	8+ j 8
Z CA, Ом	20	6+ j 8	11+ j 5	8- j 6	12- j 5	6+ j 8	16	j 20	6+ j 8	20

 

ЗАДАЧА 3.4. На рис.3.5 представлены системы несимметричных фазных напряжений и токов трехфазного приемника. Требуется определить его фазные сопротивления прямой, обратной и нулевой последовательностей.

Таблица вариантов к задаче 3.4

Первая цифра варианта	UA, B	UB, B	UC, B	a, град	b, град	Вторая цифра варианта	I A, B	IB, B	IC, B	g, град	d, град
0	120	310	220	60	200	0	50	70	90	80	90
1	140	290	200	80	180	1	100	80	60	100	80
2	160	270	190	100	160	2	80	90	70	120	100
3	180	250	150	120	140	3	40	60	80	140	70
4	200	230	130	140	90	4	90	75	60	150	120
5	220	210	110	150	80	5	65	80	55	160	190
6	240	190	120	160	100	6	30	40	50	130	140
7	260	170	100	170	70	7	60	50	40	70	160
8	280	150	180	110	120	8	40	55	35	80	180
9	300	130	230	70	190	9	70	90	110	60	200

Z N

ЗАДАЧА 3.5. Симметричный трёхфазный приёмник с сопротивлениями прямой Z ₁, обратной Z ₂ и нулевой Z ₀ последовательностей питается от симметричного источника с линейным напряжением U _л. В схеме рис.3.6 имеется участок несимметрии УН с сопротивлением Z _нс, приводящий к возникновению несимметричного режима. Рассчитать все токи и напряжение на Z _нс при наличии УН и сравнить их с соответствующими величинами при отсутствии УН.

Таблица вариантов к задаче 3.5

1-я цифра варианта	0	1	2	3	4	5	6	7	8	9
U л, В	660	380	220	127	1140	660	380	220	127	1140
Z 1, Ом	40+ j 30	40+ j 30	40+ j 30	40+ j 30	40+ j 30	80+j60	80+ j 60	80+ j 60	80+ j 60	12+ j 5
Z 2, Ом	3+ j 4	3+ j 4	3+ j 4	3+ j 4	3+ j 4	6+ j 8	6+ j 8	6+ j 8	6+ j 8	2+ j 1
Z 0, Ом	10+ j 10	10+ j 10	10+ j 10	10+ j 10	10+ j 10	20+ j 20	20+ j 20	20+ j 20	20+ j 20	1+ j
2-я цифра варианта	0	1	2	3	4	5	6	7	8	9
Z нс, Ом	∞	100	j 100	- j 100	∞	0	25	j 25	- j 25	0
Z N, Ом	10	5	∞	∞	2+ j 2	∞	∞	∞	∞	1+ j 1
Схема рис.3.6	а	а	а	а	а	б	б	б	б	б

 

ЦЕПИ НЕСИНУСОИДАЛЬНОГО ТОКА

ЗАДАЧА 4.1. К зажимам цепи рис.2.2 приложено напряжение

u(t) = U ₀ + U _{1 m} sin(w t+ y ₁ ) + U _{3 m} sin( 3 w t+ y ₃ ), B.

Определить мгновенные и действующие значения токов во всех ветвях и напряжений u ₁₂ и u ₂₃. Определить коэффициент мощности цепи, построить график тока i ₁(t), если основная частота тока   f = 50 Гц.

Амплитуды и начальные фазы напряжений отдельных гармоник приведены в таблице вариантов, а параметры элементов цепи – в таблице вариантов к задаче 2.2.

Таблица вариантов к задаче 4.1

1-я цифра варианта	U 0, B	U 1 m , B	y 1, град	U 3 m , B	y 3, град
0	32	160	+45	32	+90
1	24	140	+60	42	+30
2	60	220	+15	44	-45
3	50	127	-15	36	+45
4	48	200	-80	60	+20
5	36	180	-45	50	+60
6	60	140	+20	30	-90
7	40	310	-90	90	-20
8	30	250	+30	80	-30
9	25	190	-75	90	+75

 

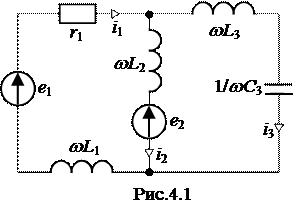
ЗАДАЧА 4.2. В цепи рис.4.1 действуют два источника ЭДС:

e ₁= E ₀ + E _{1 m} sin(w t +30° ) + E _{3 m} sin ( 3 w t -90° ), B  и   e ₂= 20 + 40 sin ( 2 w t), B.

Определить мгновенные и действующие значения токов, проверить баланс мощностей.

Таблица вариантов к задаче 4.2

Первая цифра варианта	0	1	2	3	4	5	6	7	8	9
E 0, B	80	60	40	20	30	50	70	80	60	40
E 1 m, B	100	80	70	150	90	100	200	127	220	380
E 3 m , B	50	30	26	80	40	60	90	70	100	110
Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
r 1, Ом	20	30	40	50	40	30	20	80	100	60
w L 1, Ом	10	20	15	30	25	12	18	35	40	20
w L 2, Ом	20	30	40	15	25	35	10	15	20	8
w L 3, Ом	10	15	20	25	30	35	20	40	30	25
1/ w C 3, Ом	90	135	180	120	150	100	180	210	270	240

 

 

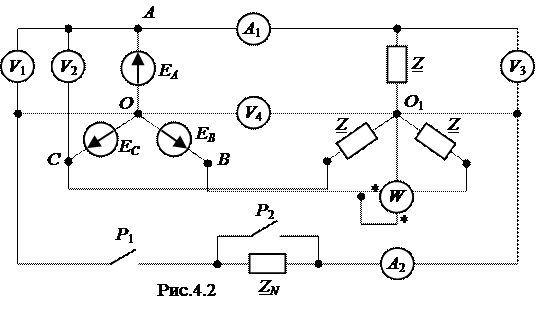
ЗАДАЧА 4.3. ЭДС симметричного трехфазного генератора, соединенного в звезду, изменяется по закону:  e _А = E _m ⁽¹⁾ sin(w t+ y ⁽¹⁾ ) + E_m ⁽³⁾ sin ( 3 w t + y ⁽³⁾ ), B.

Нагрузка, соединенная в звезду, симметрична (рис.4.2). Амплитуды и начальные фазы напряжений отдельных гармоник и параметры нагрузки заданы в таблице вариантов, а Z _N ⁽¹⁾ = 2 + j 2 Ом.

Определить показания приборов электромагнитной системы при:

а) включенных рубильниках   Р ₁  и   Р ₂.

б) включенном рубильнике   Р ₁  и выключенном рубильнике   Р ₂.

в) выключенном рубильнике   Р ₁.

Для случая а) или б) построить график линейного тока i_A(t).

Таблица вариантов к задаче 4.3

Первая цифра варианта	0	1	2	3	4	5	6	7	8	9
Em ^(1), B	180	200	310	220	240	260	280	300	210	190
y ^(1), град	15	-15	90	-30	45	-45	60	-60	-90	30
Em ^(3), B	56	60	107	100	44	48	80	90	50	72
y ^(^3^), град	-90	75	-60	45	30	0	-45	60	-75	90
Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
Z ^(1), Ом	5+ j 2	9- j 15	6- j 27	4+ j 3	5- j 12	8+ j 4	3- j 9	5+ j 3	6- j 9	12+ j 5

ЗАДАЧА 4.4. Решить задачу 4.3 в случае несимметричной нагрузки, сопротивления фаз которой приведены в таблице вариантов к задаче 4.4.

Таблица вариантов к задаче 4.4

Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
Z A ^(1), Ом	5	10	6- j 27	4+ j 3	5- j 12	8	3- j 4	5+ j 5	6- j 8	12+ j 5
Z B ^(1), Ом	4+ j 2	4- j 27	3+ j 2	6- j 9	5+ j 3	6- j 27	4+ j 3	8	8+ j 8	5- j 12
Z C ^(1), Ом	8- j 4	8+ j 2	5	6	8	4+ j 3	6	5- j 12	10	8

 

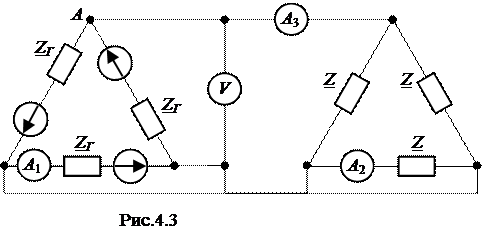
ЗАДАЧА 4.5. ЭДС симметричного трехфазного генератора, соединенного в треугольник, изменяется по закону:

e _А = E _m ⁽¹⁾ sin(w t+ y ⁽¹⁾ ) + E_m ⁽³⁾ sin( 3 w t + y ⁽³⁾ ) + E_m ⁽⁵⁾ sin( 5 w t + y ⁽⁵⁾ ), B.

Нагрузка, соединенная в треугольник, симметрична (рис.4.3). Амплитуды и начальные фазы напряжений отдельных гармоник и параметры нагрузки заданы в таблице вариантов, а внутреннее сопротивление фазы генератора    Z _Г ⁽¹⁾ = 1 + j 1 Ом.

Определить показания приборов электромагнитной системы

Таблица вариантов к задаче 4.5

Первая цифра варианта	0	1	2	3	4	5	6	7	8	9
Em ^(1), B	180	200	310	220	240	260	280	300	210	190
y ^(1), град	15	-15	90	-30	45	-45	60	-60	-90	30
Em ^(3), B	56	60	107	100	44	48	80	90	40	72
y ^(^3^), град	-90	75	-60	45	30	0	-45	60	-75	90
Em ^(5), B	56	60	107	100	44	48	80	90	40	72
y ^(^5), град	56	60	107	100	44	48	80	90	40	72
Вторая цифра варианта	0	1	2	3	4	5	6	7	8	9
Z ^(1), Ом	5+ j 2	9- j 25	6- j 27	4+ j 3	5- j 15	8- j 15	3- j 9	5+ j 3	6- j 15	12+ j 4