
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка статистических характеристик случайного процесса
Исходные данные: Объект управления – матрица
Параметры управления
По этим данным необходимо вывести реализацию случайной величины – функцию, значение которой при каждом данном значении аргумента является случайной величиной. Для этого необходимо подобрать коэффициенты регулятора P1 и P2, сгенерировать ошибки измерений и помехи внутри объекта управления, пересчитать ошибки измерений и помехи внутри объекта управления в главную систему координат и проинтегрировать систему дифференциальных уравнений n раз на отрезке [0,T]. Коэффициенты были подобраны с помощью отдельной программы АКОР. Законы генерирования ошибок измерений и помех внутри объекта управления заданы: ошибки измерений в обоих каналах СУ и помехи в первом канале отсутствуют, помехи во втором канале распределены по равномерному закону (3.1):
где А – подобранное число Чтобы пересчитать помехи внутри объекта управления в главную систему координат, необходимо сначала преобразовать матрицу В к виду B+mp:
где Bi.j – значения исходной матрицы, m1, m2 – параметры управления, P1, P2 – коэффициенты регулятора Далее определим собственные значения изменённой матрицы с помощью специальной программы пакета Mathcad (3.2):
Действительные части собственных значений изменённой матрицы получились отрицательными, значит, согласно условиям устойчивости работы системы, система работает устойчиво. Определим собственные вектора изменённой матрицы (3.3-3.4):
Для проверки можно найти матрицу D=V*BB*V-1, она должна быть диагональной и на главной диагонали должны находиться собственные значения изменённой матрицы.
Условие проверки выполнилось. Все необходимые вычисления для пересчёта в главную систему координат помех и ошибок выполнены. Формулы пересчёта ошибок измерений в главную систему координат выглядят следующим образом:
где ε1, ε2 – промежуточные переменные, P1, P2 – коэффициенты регулятора m1, m2 – параметры управления w1, w2 – изначальные ошибки измерений VO=V-1 – обратная матрица собственных векторов матрицы ВВ W1, W2 – ошибки измерений, пересчитанные в главную систему координат
Формулы пересчёта помех в главную систему координат выглядят следующим образом:
где g1, g2 – изначальные помехи внутри объекта G1, G2 – помехи, пересчитанные в главную систему координат Формулы пересчета начальных условий в главную систему координат выглядят следующим образом:
где y1, y2 – изначальные начальные условия, yy1, yy2 – начальные условия, пересчитанные в главную систему координат После записи системы в главных координатах численный метод интегрирования второго порядка точности можно представить в виде двух параллельных циклов вычислений:
где Di,j – значения диагональной матрицы D h=T/n – шаг интегрирования T – время, при котором процесс становится установившимся n – количество реализаций случайного процесса W1, W2, G1, G2, yy1, yy2 – определены выше Далее необходимо пересчитать получившуюся проинтегрированную функцию обратно в исходную систему координат:
Значения переменных состояния в конечной точке n:
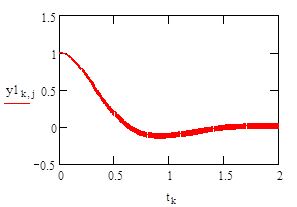
Реализации случайного процесса y1k,j и y2k,j можно отобразить с помощью графиков (см. График 3-4).
График 3 – Реализация первой переменной случайного процесса
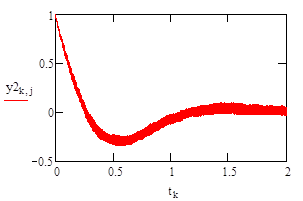
График 4 – Реализация второй переменной случайного процесса 3.1 Определение статистических характеристик системы управления в момент времени
В момент времени 1) математические ожидания переменных состояния; 2) дисперсии переменных состояния; 3) корреляционный момент; 4) нормированный корреляционный момент (коэффициент корреляции) Математическим ожиданием случайного процесса называется такая функция, значение которой при каждом данном значении аргумента равно математическому ожиданию значения этой функции при этом аргументе. Математическое ожидание случайного процесса представляет собой некоторую среднюю функцию, около которой группируются и относительно которой колеблются все возможные реализации случайного процесса. Для полученных процессов математическое ожидание находится по следующим формулам (3.5-3.6):
где Xmean, Ymean являются математическим ожиданием.
Дисперсией случайного процесса называется такая функция, значение которой при каждом данном значении аргумента равно дисперсии значения этой функции при этом аргументе. Для полученных процессов дисперсия находится по следующим формулам (3.7-3.8):
Для того чтобы учесть статистическую связь между значениями функции при различных значениях аргумента, кроме математического ожидания и дисперсии, анализируются корреляционные моменты между значениями случайного процесса в различные моменты времени. Корреляционный момент между двумя значениями функции в определённые моменты времени определяет корреляционную функцию случайного процесса. В программе корреляционный момент вычисляется по формуле (3.9):
Случайные процессы называются некоррелированными, если KOR=0 при любых значениях аргументов. В противоположном случае случайные процессы являются коррелированными. Удобно пользоваться нормированной корреляционной функцией (коэффициентом корреляции), которая является безразмерной функцией и определяется следующим образом (3.10):
где KOR – взаимный корреляционный момент DX, DY – дисперсии переменных состояния (определены выше).
3.2 Проверка гипотезы о независимости случайных величин
Для проверки гипотезы о независимости двух случайных величин по выборке XX и YY, весь диапазон значений отдельно по каждой переменной разбивается на интервалы, как это делалось при построении гистограммы при применении критерия Пирсона. Затем вычисляется статистика χn и сравнивается с табличным значением статистики (распределения) χ² с (r-1)*(s-1) степенями свободы, где r и s – количество интервалов, на которые разбит диапазон изменения каждой переменной. Так как в нашем случае диапазон изменения каждой переменной разбит на одно и то же число К, то r и s одинаковы. Гипотеза о независимости двух случайных величин отвергается с уровнем значимости α, если χn> χ². Для подсчёта статистики необходимо определить количество точек, попавших в каждый интервал по переменной XX, количество точек, попавших в каждый интервал по переменной YY, количество точек, попавших одновременно в интервалы по двум переменным (в соответствующие прямоугольники). Для этого найдём частоты попадания выборочных значений в каждый k-ый интервал по обеим переменным и количество точек, попавших одновременно в оба интервала по двум переменным. Пусть K – количество интервалов, на которые разбит диапазон изменения каждой переменной. Количество интервалов К вычисляется по правилу Стургерса. Для вычисления используется встроенная функция Mathcad (3.11):
где n – количество реализаций случайного процесса. Тогда длину интервала можно вычислить по формуле (3.12):
где Xmax, Xmin – максимальное и минимальное значение реализации случайного процесса. Для определения частоты попадания выборочных значений в каждый k-ый интервал по переменной Х воспользуемся формулой (3.13):
где k=1..K – номер интервала, uk – точки, лежащие на границе интервала, n – количество реализаций случайной величины Сумма частот всех интервалов должна быть равна количеству реализаций случайной функции n, так как все точки функции распределены на K интервалах. Это условие проверяется формулой (3.14).
Частота попадания в последний интервал равна 1. следовательно стоит объединить интервалы. После объединения крайних интервалов получаем формулу для подсчета частот попадания (3.15), которая также проверяется суммой частот попадания всех интервалов (3.16).
Рассмотрим теперь вторую переменную YY. Максимальное и минимальное значение выборки, количество интервалов в гистограмме, длина интервала определяются аналогично. Частоты попадания выборочных значений в k-ый интервал по переменной YY, определяются формулой (3.17):
где uyk – точки, лежащие на границе интервала, n – количество реализаций случайной величины, k=1..K – номер интервала. Правильность подсчёта частот попадания также проверяется суммой всех частот попадания:
Крайние интервалы объединяются аналогично переменной XX. Теперь найдём количество точек, попавших одновременно в оба интервала по двум переменным (3.18):
Преобразуем эту формулу (3.19):
Сумма точек, попавших одновременно в оба интервала по двум переменным должна быть равна количеству реализаций n:
где k и t – количество интервалов по каждой переменной соответственно. Все предварительные расчёты для вычисления статистики произведены. Далее необходимо вычислить саму статистику (3.20):
где K-2 – количество интервалов по каждой переменной после объединения крайних интервалов, Для вычисления табличной статистики необходимо высчитать количество степеней свободы (3.21):
ν=(r-1)(s-1), (3.21)
где r и s – количество интервалов по каждой переменной, то есть r=s=K-2, так как крайние интервалы были объединены. Значит, количество степеней свободы вычисляются по формуле:
Табличное значение распределения можно вычислить с помощью специальной функции Mathcad (3.22):
где α – уровень значимости Для данных двух случайных процессов XX и YY значение статистики
Очевидно, что
|
||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.039 с.) |
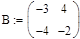
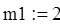
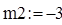
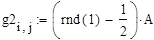 , (3.1)
, (3.1) ,
,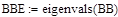 , (3.2)
, (3.2)
 , (3.3)
, (3.3)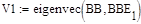 , (3.4)
, (3.4)
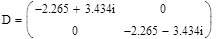
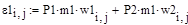 ,
,
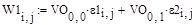

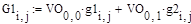
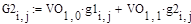


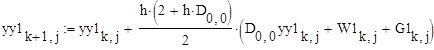 ,
,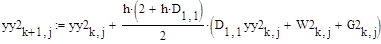 ,
,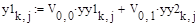 ,
,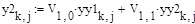 ,
,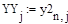 ,
, 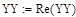
 ,
, 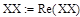
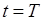
 ,
,  , (3.5-3.6)
, (3.5-3.6)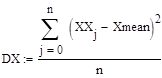 , (3.7)
, (3.7)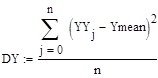 (3.8)
(3.8) (3.9)
(3.9) , (3.10)
, (3.10)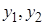 при уровне значимости a в момент времени
при уровне значимости a в момент времени 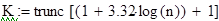 , (3.11)
, (3.11)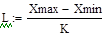 , (3.12)
, (3.12)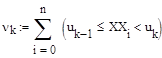 , (3.13)
, (3.13)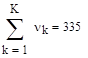 (3.14)
(3.14)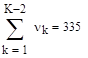 (3.16)
(3.16) , (3.17)
, (3.17)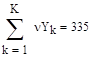
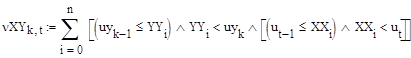 (3.18)
(3.18)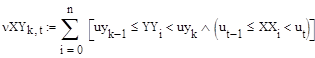 . (3.19)
. (3.19)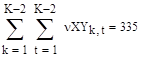
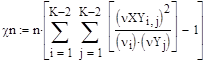 , (3.20)
, (3.20)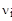 – количество точек, попавших в i-ый интервал по переменной XX,
– количество точек, попавших в i-ый интервал по переменной XX,  – количество точек, попавших в j-ый интервал по переменной YY,
– количество точек, попавших в j-ый интервал по переменной YY,  – количество точек, попавших одновременно в i-ый и j-ый интервалы по двум переменным.
– количество точек, попавших одновременно в i-ый и j-ый интервалы по двум переменным.
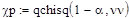 , (3.22)
, (3.22) . При этом табличное значение распределения
. При этом табличное значение распределения  .
. , следовательно, гипотеза о независимости двух случайных величин отвергается.
, следовательно, гипотеза о независимости двух случайных величин отвергается.


