
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6: функция распределения и плотность распределения нсв. Вычисление характеристик нсвСодержание книги
Поиск на нашем сайте
Плотностью распределения вероятностей f (x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.: f (x)= F ’(x) Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством: +∞ M (X)= ∫ x • f (x) dx, -∞ при условии, что этот интеграл сходится абсолютно. Дисперсия D (X) непрерывной случайной величины Х определяется равенством: +∞ D (X)= ∫ (х-М(х)2)• f (x) dx, или -∞ +∞ D (X)= ∫ х2• f (x) dx - (М(х))2 -∞ Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством:
Пример решения задач Случайная величина Х задана плотностью распределения вероятностей: 0 при х≤2, f (x)= с(х-2) при 2<х≤6, 0 при х>6. Найти: а) значение с; б) функцию распределения F (х) и построить ее график; в)Р(3≤х<5) +∞ 2 6 +∞ 6 6 ∫ f (x) dx =∫ 0 dx + ∫ c (х-2) dx +∫ 0 dx = c ∫ (х-2) dx =с(х2/2-2х) =с(36/2-12-(4/2-4))=8с; -∞ -∞ 2 6 2 2 8с=1; с=1/8. х б) Известно, что F (x)= ∫ f (x) dx -∞ Поэтому, х если х≤2, то F (x)= ∫ 0 dx =0; -∞ 2 2 х если 2<х≤6, то F (x)= ∫ 0 dx +∫ 1/8(х-2) dx =1/8(х2/2-2х) = 1/8(х2/2-2х- (4/2-4))= -∞ -∞ 2 =1/8(х2/2-2х+2)=1/16(х-2)2; 2 6 х 6 6 если х>6, то F (x)= ∫ 0 dx +∫ 1/8(х-2) dx +∫ 0 dx =1/8∫(х-2) dx =1/8(х2/2-2х) = -∞ 6 2 2 2
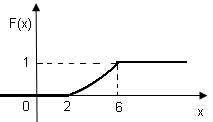
=1/8(36/2-12-(4/2+4))=1/8•8=1. Таким образом, 0 при х≤2, F (х)= (х-2)2/16 при 2<х≤6, 1 при х>6. График функции F (х) изображен на рис.
в) Р(3≤Х<5)= F (5)- F (3)=(5-2)2/16-(3-2)2/16=9/16-1/16=5/16. Задачи 1. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (0,2; 0,7) 2. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (3,3; 4,6) 3. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 4,6) 4. Случайная величина Х задана функцией распределения
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 2,9) 5. Случайная величина X задана функцией распределения
Найдите коэффициент с.
6. Случайная величина X задана функцией распределения
Найдите коэффициент с. 7. Случайная величина Х задана функцией распределения Найдите плотность вероятности 8. Случайная величина Х задана функцией распределения Найдите плотность вероятности 9. Случайная величина Х задана функцией распределения Найдите плотность вероятности 10. Случайная величина Х задана функцией распределения Найдите плотность вероятности 11. Случайная величина 12. Случайная величина 13. Случайная величина 14. Случайная величина 15. Случайная величина
16. Случайная величина 17. Случайная величина X задана функцией распределения
Найдите математическое ожидание данной случайной величины. 18. Случайная величина X задана плотностью распределения
Найдите функцию распределения 19. Случайная величина X задана плотностью распределения Найдите функцию распределения 20. Функция распределения случайной величины Х имеет вид
Найти
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.008 с.) |

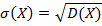
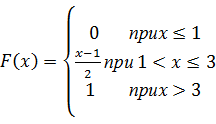
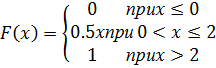

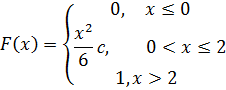

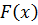 :
: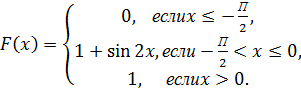
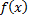 .
.
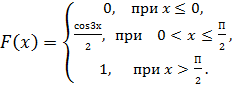
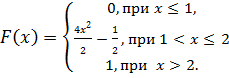 ,
,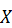 на отрезке [1,2] задана плотностью распределения
на отрезке [1,2] задана плотностью распределения 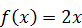 , вне этого отрезка
, вне этого отрезка 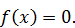 Найдите математическое ожидание данной случайной величины.
Найдите математическое ожидание данной случайной величины.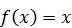 , вне этого отрезка
, вне этого отрезка 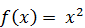 вне этого отрезка
вне этого отрезка 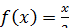 , вне этого отрезка
, вне этого отрезка 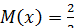 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.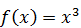 , вне этого отрезка
, вне этого отрезка 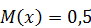 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.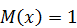 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.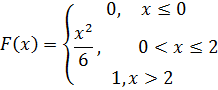
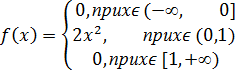
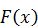 и её характеристики.
и её характеристики.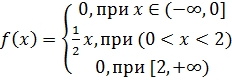
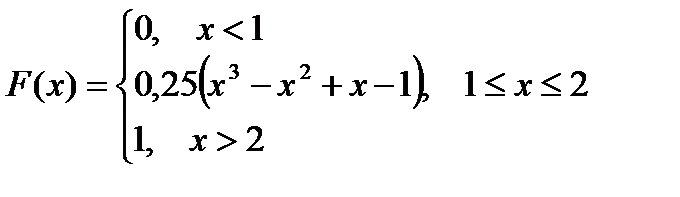
 , M(X), D(X) и P (1 < х < 1,5).
, M(X), D(X) и P (1 < х < 1,5).


