
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Теория вероятностейСодержание книги
Поиск на нашем сайте
Раздел 1. Теория вероятностей Тема 1. Решение комбинаторных задач Размещения: без повторений с повторениями Сочетания: без повторений с повторениями Перестановки: без повторений с повторениями Пример решения задач В чемпионате России по футболу участвуют 16 команд. Сколькими способами может определиться тройка призеров?
Задачи 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? 2. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин? 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек? 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать. 6. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду? 7. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире? 8. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей? 9. Сколько слов можно получить, переставляя буквы в слове ТЕОРИЯ и МАТЕМАТИКА? 10. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается? 11. Сколькими способам можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков? 12. В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений? 13. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
14. Шифр сейфа состоит только из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра? 15. Сколькими способами 4 человека могут разместиться в четырехместном купе? 16. Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски? 17. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка? 18. 30 книг стоит на книжной полке, из них 27 различных книг и одного автора три книги. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом? 19. Студенты института изучают в каждом семестре по десять дисциплин. В расписание занятий включаются каждый день по 3 дисциплины. Сколько различных расписаний может составить диспетчерская? 20. Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить? Пример решения задач Таня, Наташа, Света и Настя бросили жребий, какова вероятность, что Наташа - ведущая.
З адачи 1. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. 2. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 6 или 9. 3. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции. 4. На экзамене 50 билетов, Руслан не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет. 5. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. 6. Коля наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 3.
7. Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся. 8. В соревнованиях по художественной гимнастике участвуют: три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России. 9. Во время вероятностного эксперимента монету бросили 1000 раз, 532 раза выпал орел. На сколько частота выпадения решки в этом эксперименте отличается от вероятности этого события? 10. На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. 11. В денежно-вещевой лотерее на 100000 билетов разыгрывается 1250 вещевых и 810 денежных выигрышей. Какова вероятность денежного выигрыша? 12. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России. 13. Определите вероятность того, что при бросании кубика выпало четное число очков. 14. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3. 15. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3. 16. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A? 17. В среднем на 147 исправных дрелей приходятся три неисправные. Найдите вероятность того, что выбранная дрель исправна. 18. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными? 19. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел четна. 20. У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. Формула полной вероятности Пусть Формула Байеса Пусть Пример решения задач Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Возможны три гипотезы:
Так как вызов на линию огня любого стрелка равновозможен, то
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность гипотезы
Задачи 1. При случайном выборе карты из колоды в 36 карт возможны наступления событий: А – карта-туз В – карта-черви С – карта-картинка. Вычислите 2. При случайном выборе карты из колоды в 36 карт возможны наступления событий: А – карта-туз В – карта-черви С – карта-картинка. Вычислите 3. Из 1000 ламп 380 принадлежат к 1 партии, 270 – ко второй партии, остальные к третьей. В первой партии 4% брака, во второй - 3%, в третьей – 6%. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная. 4. Из 30 стрелков 12 попадает в цель с вероятностью 0,6, 8 - с вероятностью 0,5 и 10 – с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, поразив цель. К какой из групп вероятнее всего принадлежал этот стрелок? 5. Сотрудники отдела маркетинга полагают, что в ближайшее время ожидается рост спроса на продукцию фирмы. Вероятность этого они оценивают в 80%. Консультационная фирма, занимающаяся прогнозом рыночной ситуации, подтвердила предположение о росте спроса. Положительные прогнозы консультационной фирмы сбываются с вероятностью 95%, а отрицательные – с вероятностью 99%. Какова вероятность того, что рост спроса действительно произойдет? 6. В группе спортсменов лыжников в 2 раза больше, чем бегунов, а бегунов в 3 раза больше, чем велосипедистов. Вероятность выполнить норму для лыжника 0,9, для бегуна 0,75, для велосипедиста - 0,8. Найти вероятность того, что спортсмен, выбранный наугад, выполнит норму. 7. В двух урнах находится соответственно 4 и 5 белых и 6 и 3 чёрных шаров. Из каждой урны наудачу извлекается один шар, а затем из этих двух наудачу берется один. Какова вероятность, что это будет белый шар? 8. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
9. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. 10. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго. а) Каков процент брака на конвейере? б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере? 11. Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный? 12. В тире имеются 5 различных по точности боя винтовок. Вероятности попадания в мишень для данного стрелка соответственно равны 0,5; 0,55; 0,7; 0,75 и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки? 13. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки. 14. На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии. 15. На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%, во второй – 10%. Наудачу взятое со склада изделие оказалось не стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии. 16. Электролампы изготавливаются на трех заводах. 1-ый завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть. Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом? 17. В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того, что: а) он был подготовлен очень хорошо; 18. Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит в 2 раза больше деталей, чем второй цех, и в 4 раза больше третьего цеха. В первом цехе брак составляет 12%, во втором – 8%, в третьем – 4%. Для контроля из контейнера берется одна деталь. Какова вероятность того, что она окажется бракованной? Какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех?
19. В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара. После того, как шары во второй урне перемешались, из неё выкатился шар. Найти вероятность того, что выкатившийся из второй урны шар белый. 20. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 играных. Для игры выбираются 2 мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются ещё два мяча. Найти вероятность того, что вторая игра будет проводиться новыми мячами. Пример решения задач Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества. По условию n=400, p=0.75, q=0.25, k=280, откуда
По таблицам найдем Искомая вероятность равна: Задачи 1. Из 200 аккумуляторов за год хранения 65 выходит из строя. Наудачу выбирают 5 аккумуляторов. Определить вероятность того, что среди них 3 исправных. 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут: 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5? 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия. 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта. 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух? 7. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: а) герб выпадет три раза; б) герб выпадет один раз; в) герб выпадет не менее двух раз. 8. Вероятность того, что приставка Playstation 4 имеет скрытые дефекты, равна 0,2. На склад поступило 20 игровых приставок. Какое событие вероятнее: что в этой партии имеется две приставки со скрытыми дефектами или три? 9. Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков: а) не выпадут (выпадут 0 раз); 10. Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность. 11. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик. 12. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов. 13. Магазин получил 1000 бутылок водки. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки. 14. Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно: а) 200 раз; 15. В здании 1000 лампочек. Вероятность выхода из строя одной лампочки в течение года p =0.003. Найдем вероятность того, что в течение одного года выйдет из строя более трех ламп. 16. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз. 17. Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз. 18. В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет включено не менее 1250 и не более 1275 ламп. 19. В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую на большой перемене с вероятностью 0,1. Какова вероятность того, что в обычный учебный день: а) столовая будет заполнена не более чем на две трети; 20. В обычный учебный день вероятность присутствия студента на лекции равна 0,8. Найти вероятность того, что из 100 студентов на лекции будут присутствовать: а) 85-90%; Пример решения задач Дискретная случайная величина Х задана законом распределения:
Найти Р2, функцию распределения F (x) и построить ее график, а также M (X), D (X), σ(Х). Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то Р2=1- (0,1+0,3+0,2+0,3)=0,1 Найдем числовые характеристики случайной величины: M (X)=-1•0,1+0•0,1+1•0,3+2•0,2+3•0,3=1,5 D (X)=(-1)2 •0,1+12•3+22•0,2+32•0,3-(1,5)2=1,65
Задачи 1. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Чему равна вероятность 2. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Чему равна вероятность 3. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Чему равна вероятность 4. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 5. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 6. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 7. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 8. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 9. Закон распределения вероятностей дискретной случайной величины Х имеет вид:
Найдите 10. Дискретная случайная величина Х задана законом распределения:
Найдите функцию распределения F(x) и постройте её график. 11. Дискретная случайная величина Х задана законом распределения:
Найдите функцию распределения F(x) и постройте её график. 12. Дискретная случайная величина Х задана законом распределения:
Найдите функцию распределения F(x) и постройте её график. 13. Производится 5 независимых испытаний, в каждом из которых с одной и той же вероятностью 0,2 может наступить событие 14. Производится 5 независимых испытаний, в каждом из которых с одной и той же вероятностью 0,2 может наступить событие 15. В партии 20% нестандартных деталей. Наудачу отобрано пять деталей. Найдите математическое ожидание ДСВ 16. В партии 35% нестандартных деталей. Наудачу отобрано пять деталей. Найдите дисперсию ДСВ 17. На стеллаже библиотеки в случайном порядке расставлено 5 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу 4 учебника. Случайная величина Х-число учебников в переплете среди взятых. Составить закон распределения случайной величины. 18. В билете две задачи. Вероятность правильного решения первой задачи равна 0,8, второй-0,5. Случайная величина Х - число правильно решенных задач в билете. Составить закон распределения, вычислить математическое ожидание и дисперсию этой случайной величины, а также найти функцию распределения F(x) и построить ее график. 19. В коробке 7 фломастеров, из которых 3 фломастера уже не пишут. Наудачу берут 3 фломастера. Случайная величина Х- число пишущих фломастеров среди взятых. Составить закон распределения случайной величины. 20. Проводятся три независимых испытания, в каждом из которых вероятность наступления некоторого события постоянна и равна p. Пусть X – число появлений события A в этом опыте. Найти D(X), если известно, что M(X) = 2,1.
Пример решения задач Случайная величина Х задана плотностью распределения вероятностей: 0 при х≤2, f (x)= с(х-2) при 2<х≤6, 0 при х>6. Найти: а) значение с; б) функцию распределения F (х) и построить ее график; в)Р(3≤х<5) +∞ 2 6 +∞ 6 6 ∫ f (x) dx =∫ 0 dx + ∫ c (х-2) dx +∫ 0 dx = c ∫ (х-2) dx =с(х2/2-2х) =с(36/2-12-(4/2-4))=8с; -∞ -∞ 2 6 2 2 8с=1; с=1/8. х б) Известно, что F (x)= ∫ f (x) dx -∞ Поэтому, х если х≤2, то F (x)= ∫ 0 dx =0; -∞ 2 2 х если 2<х≤6, то F (x)= ∫ 0 dx +∫ 1/8(х-2) dx =1/8(х2/2-2х) = 1/8(х2/2-2х- (4/2-4))= -∞ -∞ 2 =1/8(х2/2-2х+2)=1/16(х-2)2; 2 6 х 6 6 если х>6, то F (x)= ∫ 0 dx +∫ 1/8(х-2) dx +∫ 0 dx =1/8∫(х-2) dx =1/8(х2/2-2х) = -∞ 6 2 2 2 =1/8(36/2-12-(4/2+4))=1/8•8=1. Таким образом, 0 при х≤2, F (х)= (х-2)2/16 при 2<х≤6, 1 при х>6. График функции F (х) изображен на рис.
в) Р(3≤Х<5)= F (5)- F (3)=(5-2)2/16-(3-2)2/16=9/16-1/16=5/16. Задачи 1. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (0,2; 0,7) 2. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (3,3; 4,6) 3. Случайная величина Х задана функцией распределения Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 4,6) 4. Случайная величина Х задана функцией распределения
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 2,9) 5. Случайная величина X задана функцией распределения
Найдите коэффициент с.
6. Случайная величина X задана функцией распределения
Найдите коэффициент с. 7. Случайная величина Х задана функцией распределения Найдите плотность вероятности 8. Случайная величина Х задана функцией распределения Найдите плотность вероятности 9. Случайная величина Х задана функцией распределения Найдите плотность вероятности 10. Случайная величина Х задана функцией распределения Найдите плотность вероятности 11. Случайная величина 12. Случайная величина 13. Случайная величина 14. Случайная величина 15. Случайная величина 16. Случайная величина 17. Случайная величина X задана функцией распределения
Найдите математическое ожидание данной случайной величины. 18. Случайная величина X задана плотностью распределения
Найдите функцию распределения 19. Случайная величина X задана плотностью распределения Найдите функцию распределения 20. Функция распределения случайной величины Х имеет вид
Найти
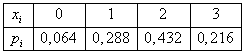
Пример решения задач Построить ряд распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,6. Найти среднее число попаданий и дисперсию.
Искомый закон распределения:
Контроль: 0,064 + 0,288 + 0,432 + 0,216 = 1
1. Случайная величина Х равномерно распределена в интервале (-1;2). Найдите: а) плотность распределения f(x); б)функции распределения F(x); в)числовые характеристики; г)вероятность Р(4<х<6). 2. Случайная величина Х равномерно распределена в интервале (2;8). Найдите: а) плотность распределения f(x); б)функции распределения F(x); в)числовые характеристики; г)вероятность Р(3<х<9). 3. Непрерывная случайная величина Х задана плотностью распределения вероятностей: а) Назовите закон распределения рассматриваемой случайной величины. б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х. в) Найдите основные характеристики 4. Непрерывная случайная величина Х задана плотностью распределения вероятностей: а) Назовите закон распределения рассматриваемой случайной величины. б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х. в) Найдите основные характеристики 5. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 10 и 4. Найдите: а) плотность распределения б) вероятность того, что в результате испытания Х примет значение из интервала (8;14). 6. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 4 и 2. Найдите: а) плотность распределения б) вероятность того, что в результате испытания Х примет значение из интервала (3;5). 7. Случайная величина Х распределена нормально с M(X)=0 и D(X)=1. Какое из событий: |Х|≤0,6 или |Х|≥0,6 имеет большую вероятность? 8. Сл
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.97.20 (0.016 с.) |

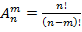
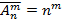
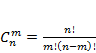
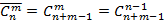
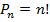
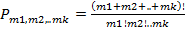
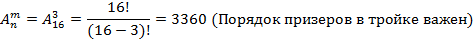
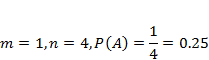
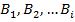 — полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле:
— полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле: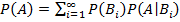
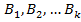 — полная группа событийи A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие
— полная группа событийи A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие 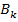 , если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:
, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле: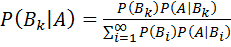
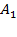 - на линию огня вызван первый стрелок,
- на линию огня вызван первый стрелок,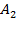 - на линию огня вызван второй стрелок,
- на линию огня вызван второй стрелок,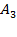 - на линию огня вызван третий стрелок.
- на линию огня вызван третий стрелок.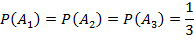
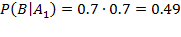
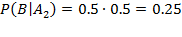
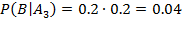
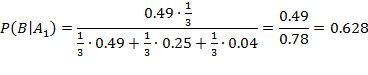
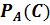
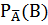
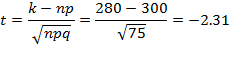
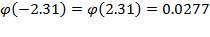 .
.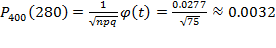
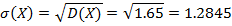
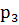
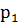
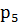
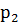
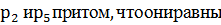 , M(X),D(X) и σ(Х).
, M(X),D(X) и σ(Х).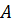 . Найдите математическое ожидание ДСВ -число наступления события
. Найдите математическое ожидание ДСВ -число наступления события 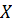 - числа нестандартных деталей среди пяти отобранных.
- числа нестандартных деталей среди пяти отобранных.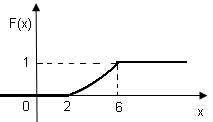
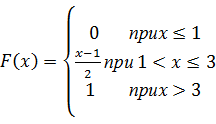
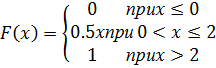

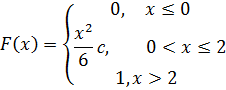

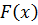 :
: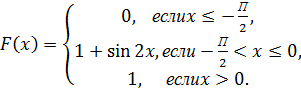
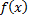 .
.
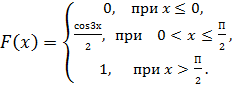
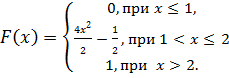 ,
,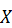 на отрезке [1,2] задана плотностью распределения
на отрезке [1,2] задана плотностью распределения 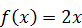 , вне этого отрезка
, вне этого отрезка 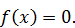 Найдите математическое ожидание данной случайной величины.
Найдите математическое ожидание данной случайной величины.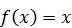 , вне этого отрезка
, вне этого отрезка 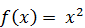 вне этого отрезка
вне этого отрезка 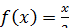 , вне этого отрезка
, вне этого отрезка 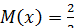 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.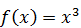 , вне этого отрезка
, вне этого отрезка 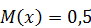 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.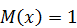 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.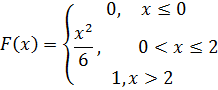
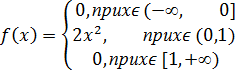
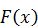 и её характеристики.
и её характеристики.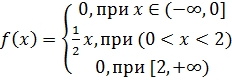
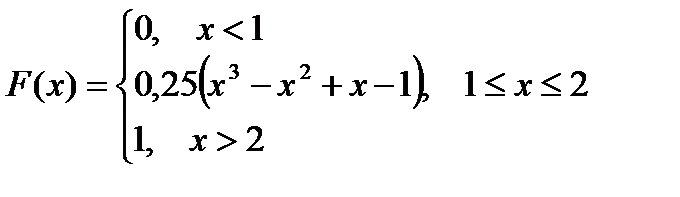
 , M(X), D(X) и P (1 < х < 1,5).
, M(X), D(X) и P (1 < х < 1,5).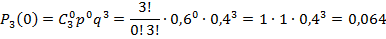
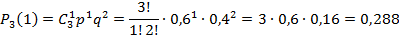
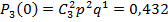
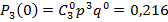
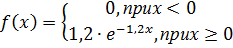
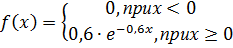
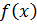 ;
;


