Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Вычисление вероятностей по формуле Бернулли и формулам ЛапласаСодержание книги
Поиск на нашем сайте
Формула Бернулли: Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико, а число p отлично от 0 и 1, тогда:
Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоватьс. Интегральная теорема Лапласа Если n – велико, а р – отлично от 0 и 1, то
где Пример решения задач Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества. По условию n=400, p=0.75, q=0.25, k=280, откуда
По таблицам найдем Искомая вероятность равна: Задачи 1. Из 200 аккумуляторов за год хранения 65 выходит из строя. Наудачу выбирают 5 аккумуляторов. Определить вероятность того, что среди них 3 исправных. 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут: 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5? 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия. 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта. 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух? 7. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: а) герб выпадет три раза; б) герб выпадет один раз; в) герб выпадет не менее двух раз. 8. Вероятность того, что приставка Playstation 4 имеет скрытые дефекты, равна 0,2. На склад поступило 20 игровых приставок. Какое событие вероятнее: что в этой партии имеется две приставки со скрытыми дефектами или три?
9. Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков: а) не выпадут (выпадут 0 раз); 10. Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность. 11. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик. 12. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов. 13. Магазин получил 1000 бутылок водки. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки. 14. Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно: а) 200 раз; 15. В здании 1000 лампочек. Вероятность выхода из строя одной лампочки в течение года p =0.003. Найдем вероятность того, что в течение одного года выйдет из строя более трех ламп. 16. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз. 17. Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз. 18. В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет включено не менее 1250 и не более 1275 ламп. 19. В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую на большой перемене с вероятностью 0,1. Какова вероятность того, что в обычный учебный день: а) столовая будет заполнена не более чем на две трети; 20. В обычный учебный день вероятность присутствия студента на лекции равна 0,8. Найти вероятность того, что из 100 студентов на лекции будут присутствовать: а) 85-90%;
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.009 с.) |

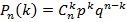
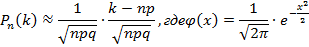
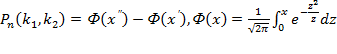 - функция Лапласа.
- функция Лапласа.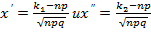
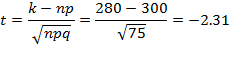
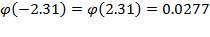 .
.