
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7: виды распределений дсв и нсвСодержание книги
Поиск на нашем сайте
Для биномиального распределения: · математическое ожидание M(X) = np, · дисперсия D(X) = npq, · среднее квадратическое отклонение σ(Х) = √D(X) Геометрическое распределение Производится серия испытаний. Случайная величина - количество испытаний до появления первого успеха (например, бросание мяча в корзину до первого попадания). Закон распределения имеет вид:
Равномерный закон распределения Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а; b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f (x) постоянная на этом интервале и равна 0 вне его, т.е. 0 при х≤а, f (х)= 0 при х≥ b.
Показательный (экспоненциальный) закон распределения Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если функция плотности распределения вероятностей имеет вид: 0 при х<0, f (х)= λ е- λ х при х≥0. Функция распределения случайной величины Х, распределенной по показательному закону, задается формулой: 0 при х≤3, F (х)= 1- e - λ х при х≥0. Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:
M(X)= Пример решения задач Построить ряд распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,6. Найти среднее число попаданий и дисперсию.
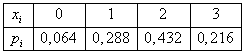
Искомый закон распределения:
Контроль: 0,064 + 0,288 + 0,432 + 0,216 = 1
1. Случайная величина Х равномерно распределена в интервале (-1;2). Найдите: а) плотность распределения f(x); б)функции распределения F(x); в)числовые характеристики; г)вероятность Р(4<х<6). 2. Случайная величина Х равномерно распределена в интервале (2;8). Найдите: а) плотность распределения f(x); б)функции распределения F(x); в)числовые характеристики; г)вероятность Р(3<х<9). 3. Непрерывная случайная величина Х задана плотностью распределения вероятностей:
а) Назовите закон распределения рассматриваемой случайной величины. б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х. в) Найдите основные характеристики 4. Непрерывная случайная величина Х задана плотностью распределения вероятностей: а) Назовите закон распределения рассматриваемой случайной величины. б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х. в) Найдите основные характеристики 5. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 10 и 4. Найдите: а) плотность распределения б) вероятность того, что в результате испытания Х примет значение из интервала (8;14). 6. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 4 и 2. Найдите: а) плотность распределения б) вероятность того, что в результате испытания Х примет значение из интервала (3;5). 7. Случайная величина Х распределена нормально с M(X)=0 и D(X)=1. Какое из событий: |Х|≤0,6 или |Х|≥0,6 имеет большую вероятность? 8. Случайная величина Х распределена нормально с M(X)=0 и D(X)=1.Из какого интервала (-0,5;-0,1) или (1;2) при одном испытании она примет значение с большей вероятностью? 9. Случайная величина Х распределена нормально с M(X)=12,6. Вероятность попадания случайной величины в интервал (11,4;13,8) равна 0,6826. Найдите среднее квадратическое отклонение σ. 10. 30% изделий, выпускаемых данным предприятием, нуждается в дополнительной регулировке. Наудачу отобрано 200 изделий. Найти среднее значение и дисперсию случайной величины X – числа изделий в выборке, нуждающихся в регулировке. 11. Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10? 12. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты? Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
13. Пусть X – случайная величина, подчиненная нормальному закону с математическим ожиданием 14. Все значения равномерно распределенной случайной величины лежат на отрезке [2,8]. Найти вероятность попадания случайной величины в промежуток (3,5). 15. Монета брошена 6 раз. Найдите дисперсию ДСВ -числа появления «решки» при десяти бросаниях монеты. 16. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель 17. Составим ряд распределения случайной величины X – числа попаданий при 5 выстрелах, если вероятность попадания при одном выстреле равна 0,8. 18. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный законраспределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных.Найти математическое ожидание и дисперсию случайной величины. 19. Написать биномиальный закон распределения дискретной случайной величины X— числа появлении «герба» при двух бросаниях монеты. 20. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется: а) 5 бракованных; б) хотя бы одна бракованная.
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.172.207 (0.01 с.) |


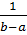 при a <х< b,
при a <х< b,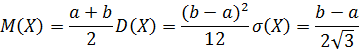
 , D(X)=
, D(X)= 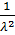 , σ (Х)=
, σ (Х)= 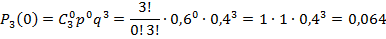
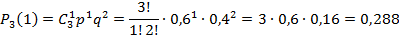
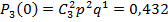
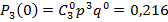
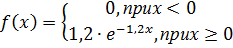
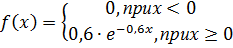
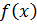 ;
;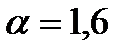 и средним квадратическим отклонением
и средним квадратическим отклонением 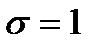 . Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?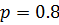 . Найдите вероятность того, что попадание произойдет при третьем выстреле.
. Найдите вероятность того, что попадание произойдет при третьем выстреле.


