Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Математическая статистикаСодержание книги
Поиск на нашем сайте
Тема1: Построение для заданной выборки ее графической гистограммы, расчет ее числовых характеристик Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки (xi; ni) соединяют отрезками прямых и получают полигон частот. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты). Площадь i - го частичного прямоугольника равна hni / h = ni - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Площадь i - го частичного прямоугольника равна hWi / h = Wi - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. Отношение частоты ni интервала к ширине hi этого интервала называют абсолютной плотностью распределения для i-го интервала. Будем обозначать ее символом pi. Абсолютная плотность распределения - это частота, приходящаяся на единицу ширины интервала. Относительной плотностью распределения πi для i-го интервала называют отношение относительной частоты интервала к его ширине. Пример решения задач При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот. 1) Статистический ряд распределения частот:
2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Напишем распределение относительных частот:
Контроль: 0,1+0,2+0,4+0,1+0,2=1. Задачи 1. Попросите 15–25 студентов вашей группы назвать свой рост, после чего: 1) запишите полученные выборочные значения; 2) постройте вариационный ряд; 3) постройте график эмпирической функции распределения; 4) сгруппировав выборочные значения по интервалам вида 180 ± 2.5 см, постройте гистограмму и полигон частот; 5) посмотрите, как изменятся гистограмма и полигон частот при увеличении ширины интервалов до 10 см; 6) предложите несколько статистик для оценки среднего роста студента и найдите численные значения этих оценок по выборочным данным.
2. В результате измерения диаметров 200 валиков из партии, изготовленной одним станком-автоматом, получены отклонения измеренных диаметров от номинала (в микрометрах). Сгруппированные данные представлены в виде интервального статистического ряда. Постройте гистограмму и полигон частот. Найдите выборочное среднее, выборочную дисперсию и исправленную выборочную дисперсию. 3. При помощи вольтметра, точность которого характеризуется средним квадратичным отклонением 0.2 В, произведено 10 измерений напряжения электрической батареи. Найдите 95%-й доверительный интервал для истинного значения напряжения, если среднее арифметическое результатов наблюдений x = 50.2 В. Предполагается, что контролируемый признак имеет нормальный закон распределения. Раздел 3. Теория графов Тема 1: Способы задания графов. Характеристики графов Виды графов Матрицей смежности вершин графа G =(S,U) порядка n называется квадратная матрица порядка n, строки и столбцы которой соответствуют вершинам графа, где элементы Матрицей смежности дуг графа G =(S,U),где Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строится по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром. 1. Неориентированный граф a. 1 – вершина инцидентна ребру b. 0 – вершина не инцидентна ребру 2. Ориентированный граф
a. 1 – вершина инцидентна ребру, и является его началом b. 0 – вершина не инцидентна ребру c. -1 – вершина инцидентна ребру, и является его концом Задачи 1. Перечислите мультиграфы, простые графы, двудольные и полные графы. Назовите порядок каждого графа. 2. Найдите степени вершин графов, изображенных на рисунке, полустепени исхода и захода. 3. Для графа, изображенного на рисунке построить матрицу смежности вершин, дуг и матрицу инцидентности.
4. Приведите примеры (незамкнутого) маршрута, замкнутого маршрута, цепи (не являющейся простой), простой цепи, цикла (не являющегося простым), простого цикла. 5. Найти эксцентриситеты вершин, радиусы и диаметры графа G, изображенного на рисунке и центральные вершины. 6. Для данного графа постройте матрицу смежности дуг, вершин, матрицу инцидентности. Найдите эксцентриситеты вершин, радиус графа, центр графа и его центральные вершины. 7. В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий? 8. На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкопожатий было сделано? 9. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий? 10. В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось? 11. В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и восемь непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е. Можно ли по этим дорогам проехать из А в Г? 12. В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд? 13. Из наборного полотна взяли 2 карточки с цифрой 1 и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек? 14. В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым 15. На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому. 16. У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо? 17. Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:
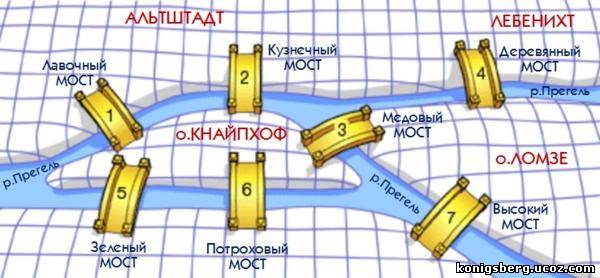
2. учитель литературы может дать один, либо второй, либо третий урок; 18. Из трех человек, стоящих рядом, один всегда говорит правду (правдолюб), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит либо правду, либо ложь (дипломат). У стоящего слева спросили: "Кто стоит рядом с тобой?". Он ответил: "Правдолюб". Стоящему в центре задали вопрос: "Кто ты?", и он ответил: "Я дипломат". Когда у стоящего справа спросили: "Кто стоит рядом с тобой?", он сказал: "Лжец". Кто где стоял? 19. 1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе - семь мостов, расположенных так, как показано на рисунке ниже. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках - проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог. Разрешите эту проблему с помощью графа. Составьте для него матрицу смежности вершин. Найдите радиус, диаметр и центр этого графа.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.238.150 (0.012 с.) |

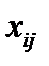 равны числу дуг, идущих из i -ой вершины, в j -ую.
равны числу дуг, идущих из i -ой вершины, в j -ую.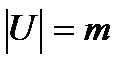 , называется квадратная матрица, порядка m, элементы которой
, называется квадратная матрица, порядка m, элементы которой 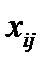 равны единице, если дуга
равны единице, если дуга 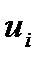 непосредственно предшествует дуге
непосредственно предшествует дуге 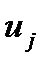 , и равны нулю в остальных случаях.
, и равны нулю в остальных случаях.