
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл как предел интегральных сумм.
Пусть функция Опр. Разбиением
Выберем произвольные точки
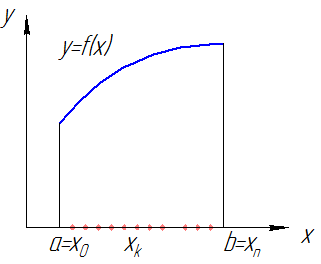 Опр. Интегральной суммой функции Опр. Интегральной суммой функции 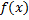 , соответствующей разбиению , соответствующей разбиению 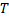 отрезка отрезка 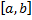 и выбору точек и выбору точек  ( (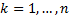 ) называется величина ) называется величина  (см. рис. 1). (см. рис. 1).
Опр. Определенным интегралом функции Обозн.:
Тогда масса неоднородного стержня: Опр. Если для функции Теорема (необходимое условие интегрируемости.) Пусть функция Теорема (достаточное условие интегрируемости 1). Непрерывная на Теорема (достаточное условие интегрируемости 2). Пусть Геометрическая интерпретация определенного интеграла.
  . .
При
Свойства определенного интеграла 1. Линейность Пусть функции a. функция b. функция Док-во: a. составим интегральную сумму для функции
Тогда
b. Аналогично
Тогда
2. Аддитивность (см. рис. 3). Пусть функция
Док-во: Рассмотрим разбиение

Т.е.
Замечание. Если
Теорема (об оценке определенного интеграла) Пусть Тогда Док-во: При
 Геометрическая интерпретация: Геометрическая интерпретация:
Следстви e (интегрирование неравенства). Пусть Док-во: рассмотрим функцию
Пример.
Теорема (о среднем значении для определенного интеграла). Пусть Док-во: т.к.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.252.199 (0.012 с.) |
 .
.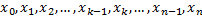 , где
, где 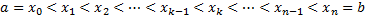 .
.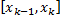 – элементарный отрезок (
– элементарный отрезок (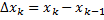 ,
,  – диаметр разбиения
– диаметр разбиения 
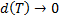 интегральных сумм
интегральных сумм 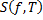 , если он существует и не зависит от способа разбиения отрезка и выбора точек
, если он существует и не зависит от способа разбиения отрезка и выбора точек 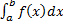 , т.е.
, т.е.
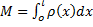 ; координата точки:
; координата точки:  .
.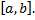
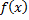 непрерывна на
непрерывна на  , тогда
, тогда 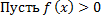 , непрерывна на
, непрерывна на 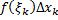 – площадь прямоугольника
– площадь прямоугольника 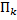 со сторонами
со сторонами 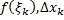 (см. рис. 2).
(см. рис. 2).
 сверху, осью
сверху, осью 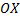 снизу и прямыми
снизу и прямыми  .
.
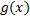 интегрируемы на
интегрируемы на 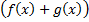 интегрируема на
интегрируема на 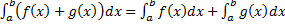
 (
(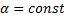 ) интегрируема на
) интегрируема на 
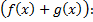
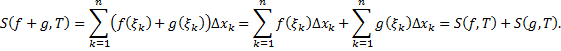
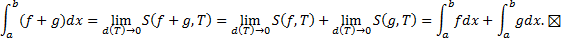
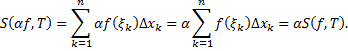
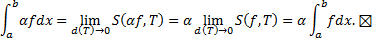
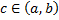 , тогда
, тогда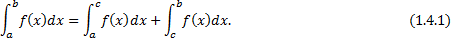
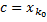 для некоторого
для некоторого 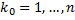 . Ему соответствуют разбиения отрезков
. Ему соответствуют разбиения отрезков 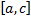 и
и 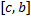 , соответственно,
, соответственно, 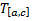 и
и 
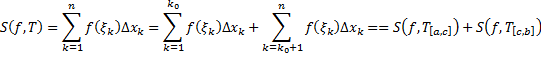
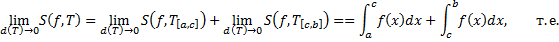
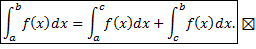
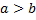 , то по определению
, то по определению 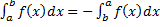 ,
,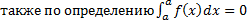 . Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек
. Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек  ,
, 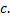
 .
.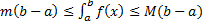 .
.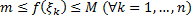 , то
, то 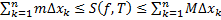 ,
, 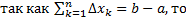
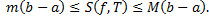
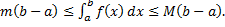

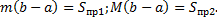
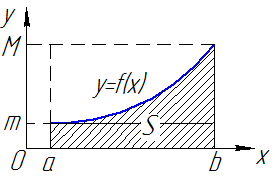
 (площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4).
(площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4). на
на 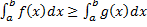 .
. на
на 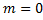 . По теореме об оценке
. По теореме об оценке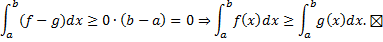
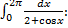 т.к.
т.к. 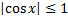 , то
, то 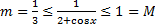 . По теореме об оценке
. По теореме об оценке 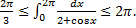
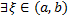 такая, что
такая, что  .
.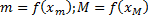 ,
, 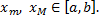 По теореме об оценке
По теореме об оценке 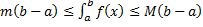 , (равенство возможно только для
, (равенство возможно только для  т.е. для непрерывных функций, отличных от константы
т.е. для непрерывных функций, отличных от константы 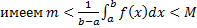 . По теореме о промежуточном значении непрерывной функции:
. По теореме о промежуточном значении непрерывной функции:  . Возьмем
. Возьмем 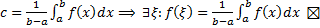 .
.


