Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральное исчисление функций одного переменногоСтр 1 из 13Следующая ⇒
Интегральное исчисление функций одного переменного
Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов.
Опр. Функция Пример. Теорема 1 (об арифметических свойствах первообразной). Пусть Док-во: Теорема 2 (об общем виде первообразной). Пусть
Док-во: т.к. Опр. Совокупность всех первообразных функции Обозн.: Пусть Пример. Свойства неопределенного интеграла: 1. 2. 3. 4. Док-во: 1. 2. 3. Т.к. 4. Пусть Тогда функция Таблица интегралов: 1. 2. 3.
4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. Примеры.
Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций.
Подведение под знак дифференциала. Пусть Рассмотрим сложную функцию
Примеры. 1. 2. 3.
Замена переменной. Поменяем в (1.2.1) местами где Пусть
Т.е.
Пример.
Интегрирование по частям Пусть функции Док-во:
Примеры. 1. 2. 3. т.е.
Интегрирование выражений, содержащих квадратный трехчлен I. Выделим полный квадрат, получим табличный интеграл (10-13) Примеры. 1. 2. II. Выделим в числителе производную квадратного трехчлена
где Аналогично
где Примеры. 1. 2. Интегрирование иррациональных функций. I. Замена Пример.
II. Замена Пример.
III. Выделив полный квадрат, получим интеграл одного из видов: a) Замена Пример.
b) Замена Пример.
c) Замена Пример.
Примеры интегралов, не выражающихся через элементарные функции:
Определенный интеграл, его механический и геометрический смысл, теорема существования. Линейность и аддитивность определенного интеграла.
Док-во: a. составим интегральную сумму для функции
Тогда
b. Аналогично
Тогда
2. Аддитивность (см. рис. 3). Пусть функция
Док-во: Рассмотрим разбиение

Т.е.
Замечание. Если
Теорема (об оценке определенного интеграла) Пусть Тогда Док-во: При
 Геометрическая интерпретация: Геометрическая интерпретация:
Следстви e (интегрирование неравенства). Пусть Док-во: рассмотрим функцию
Пример.
Теорема (о среднем значении для определенного интеграла). Пусть Док-во: т.к.
Формула Ньютона-Лейбница. Пусть Док-во: пусть
Пример.
Свойство линейности. Если
Аналогично для Геометрический смысл: при
Рис. 15
Рис. 16 Свойство линейности. Если
Примеры несобственных интегралов с несколькими особыми точками 1. Исходный интеграл сходится, если сходятся оба интеграла в правой части: a.
b.
(несобственный интеграл 2-го рода a. b. Значит,
a. При b. При Таким образом исходный интеграл расходится. Объемы тел вращения.
Рис. 26 Фигура, ограниченная линиями Найдем объем
Ту же фигуру вращаем вокруг оси
Рис. 27 Рассмотрим малый отрезок
Тогда
Суммируя по тонким "слоям", получим
Общий случай:
Таким образом получаем для вращения фигуры, ограниченной линиями
При вращении фигуры, ограниченной линиями
Рис. 28
Длина дуги кривой. Пусть дуга
Функции
Рассмотрим переменную точку
Дифференциал дуги
Случай плоской кривой:
Случай графика функции
Случай кривой, заданной в полярных координатах:
Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ.
Рис. 30 Рассмотрим на плоскости семейство эллипсов
Найдем семейство кривых, ортогональных семейству эллипсов. 1. Составим дифференциальное уравнение (ДУ) семейства эллипсов. Продифференцируем уравнение (2.1.1), считая
Отсюда
2. Составим ДУ ортогонального семейства. В т.
3. Найдем уравнение ортогонального семейства:
Получаем Линейные ДУ (ЛДУ) n-го порядка: однородные (ЛОДУ) и неоднородные (ЛНДУ). Теорема существования и единственности решения. Линейный дифференциальный оператор. Свойства линейного дифференциального оператора и линейность пространства решений ЛОДУ.
ЛДУ n-го порядка (неоднородное):
Коэффициенты
(2.6.1)– ЛНДУ
Задача Коши для ДУ: найти частные решения, удовлетворяющие начальным условиям:
где Теорема существования и единственности решения задачи Коши для ЛДУ Пусть Рассмотрим левую часть ЛДУ (2.6.1) и (2.6.10) – дифференциальный оператор
Покажем, что
Таким образом, Операторная форма ЛДУ: ЛНДУ:
ЛОДУ:
Док-во: (от противного) Пусть
Ее определитель Рассмотрим частное решение ЛОДУ
Оно удовлетворяет в т.
Рассмотрим частное решение ЛОДУ
Оно удовлетворяет в т.
Таким образом, частные решения ЛОДУ Т.е. Замечание. Пусть
Не может иметь вид (см. рис. 39, 40):
Фазовая плоскость. Рассмотрим
Пусть вектор-функция
Кривая Касательный вектор к фазовой кривой в произвольной точке (см. рис. 41):
Рис. 41 Рассмотрим
Таким образом фазовые кривые системы
Пример.
ДУ фазовых кривых:
Рис. 42 Опр. Равенство
называется первым интегралом системы
1. Функция 2. Для
Первый интеграл позволяет понизить число уравнений в системе. Пусть в т.
Подставив
Чтобы полностью решить систему
Независимость первых интегралов означает, что ни один из них не может быть выражен через остальные. Система Симметричная форма записи нормальных систем ДУ:
Получив из симметричной формы системы интегрируемые комбинации (полные дифференциалы), можно найти 1-е интегралы. При нахождении интегрируемых комбинаций удобно использовать следующее свойство пропорций:
Пример 1.
Симмметричная форма системы:
По свойству пропорций получаем
Аналогично
Пример 2.
Для автономной системы найдем два независимых 1-х интеграла, не содержащих
Симметричная форма системы:
Чтобы найти второй 1-й интеграл запишем симметричную форму системы в виде
Таким образом, найденные первые интегра
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.94.187 (0.289 с.) |
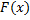 называется первообразной функции
называется первообразной функции 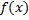 на
на 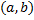 , если
, если 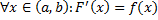 .
.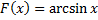 – первообразная функции
– первообразная функции  на интервале
на интервале 
 и
и 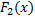 – первообразные функций
– первообразные функций  и
и  соответственно. Тогда функция
соответственно. Тогда функция 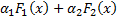 – первообразная функции
– первообразная функции 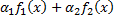 (
(
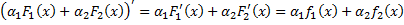 , т.е. функция
, т.е. функция 

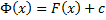 , где
, где 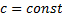
 , то
, то 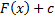 – тоже первообразная функции
– тоже первообразная функции 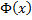 – первообразная функции
– первообразная функции 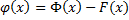 :
: 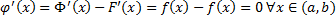 . Рассмотрим произвольные
. Рассмотрим произвольные 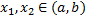 .
.  т.е.
т.е. 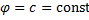 . Значит,
. Значит, 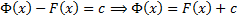
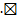
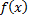 .
.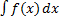 .
. , где
, где 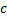 – произвольная постоянная.
– произвольная постоянная.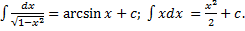

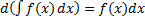
 или
или 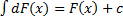
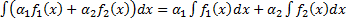 , где
, где 
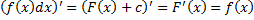 , где
, где 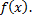
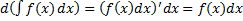 .
.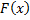 – первообразная
– первообразная 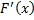 , то
, то 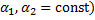 . Отсюда
. Отсюда 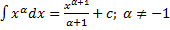
 . (Т.к. при
. (Т.к. при 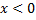
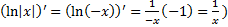
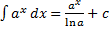 (
(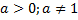 )
)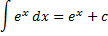
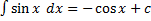

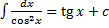
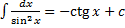
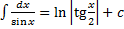
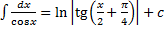
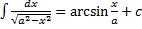 ,
, 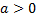
 ,
, 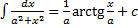 ,
, или
или 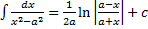 (высокий логарифм)
(высокий логарифм)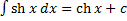
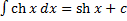
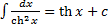
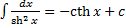
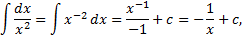

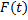 – первообразная функции
– первообразная функции 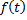 на
на 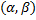 , т.е.
, т.е. 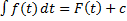 . Рассмотрим замену
. Рассмотрим замену 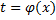 , где
, где  – дифференцируемая на
– дифференцируемая на  .
.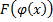 ,
, 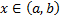 .
. , т.е.
, т.е. 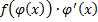 , т.е.
, т.е.  , или
, или 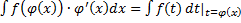 , или
, или 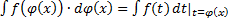 ,
,
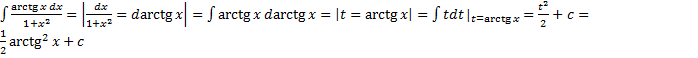
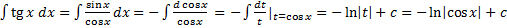
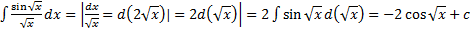 .
.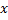 и
и 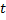 :
:  ,
,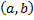 ,
, 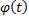 дифференцируема на
дифференцируема на 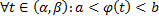 .
.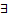 обратная функция
обратная функция 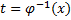 . Заменим
. Заменим 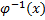 :
: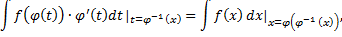
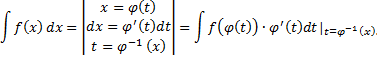
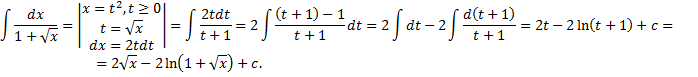
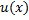 и
и  дифференцируемы на
дифференцируемы на  , т.е.
, т.е. 
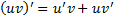 , т.е.
, т.е. 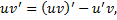
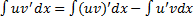 , т.е.
, т.е. 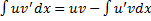 ,
,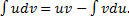
 .
.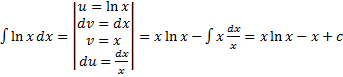 .
.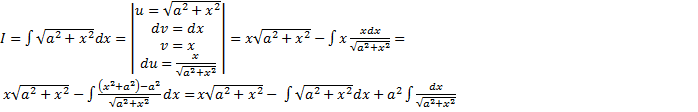 ,
, , т.е.
, т.е.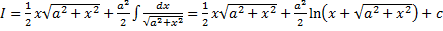 .
. ,
, 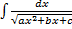 .
.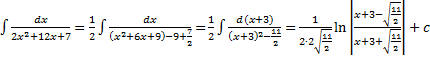 .
.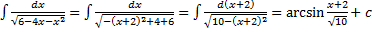 .
.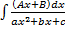 ,
, 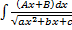 .
.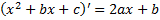 , т.е. представим числитель в виде
, т.е. представим числитель в виде 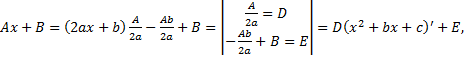
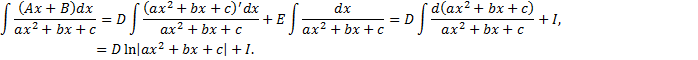
 – находится с помощью выделения полного квадрата.
– находится с помощью выделения полного квадрата.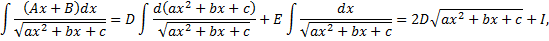
 .
.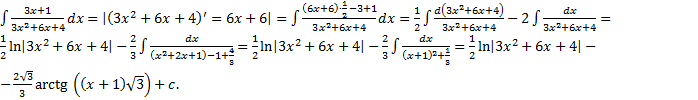
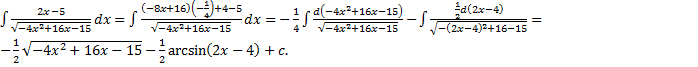
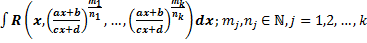 .
.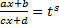 ,
, 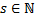 –общий знаменатель
–общий знаменатель  (Н.О.К.
(Н.О.К.  ).
).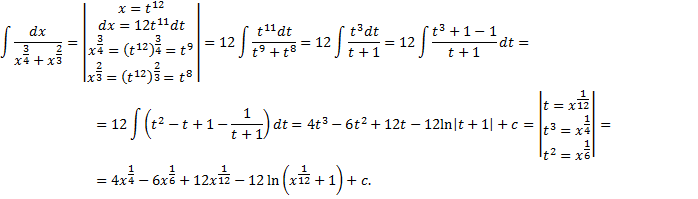

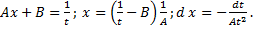
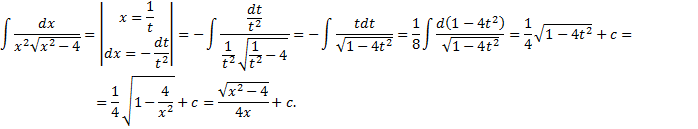
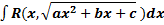 .
.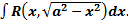
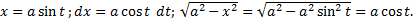
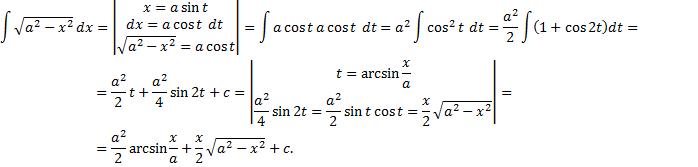
 .
. .
.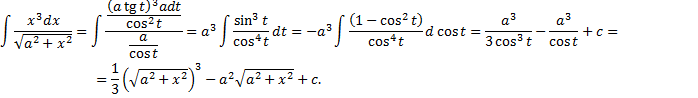
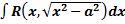 .
.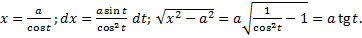
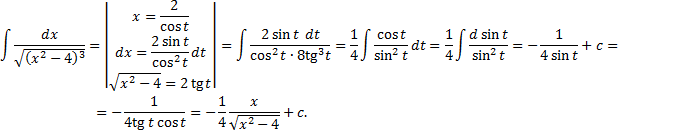
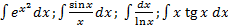 («неберущиеся» интегралы).
(«неберущиеся» интегралы).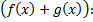
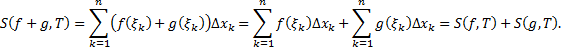
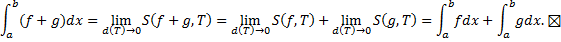
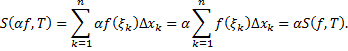
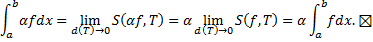
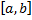 , точка
, точка 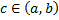 , тогда
, тогда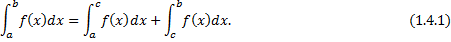
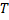 отрезка
отрезка 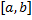 такое, что
такое, что 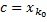 для некоторого
для некоторого 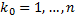 . Ему соответствуют разбиения отрезков
. Ему соответствуют разбиения отрезков 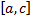 и
и 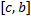 , соответственно,
, соответственно, 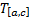 и
и 
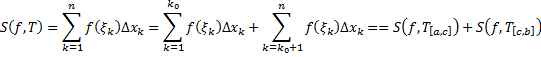
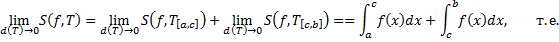
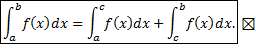
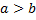 , то по определению
, то по определению 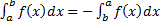 ,
,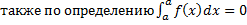 . Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек
. Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек  ,
, 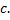
 .
.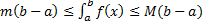 .
. . Т.к.
. Т.к. 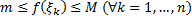 , то
, то 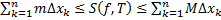 ,
, 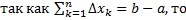
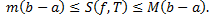
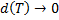 получим
получим 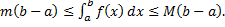
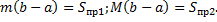
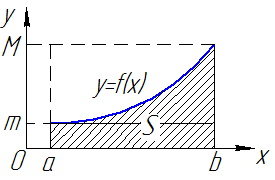
 (площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4).
(площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4). на
на 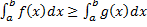 .
. на
на 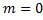 . По теореме об оценке
. По теореме об оценке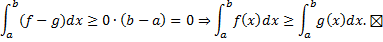
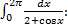 т.к.
т.к. 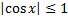 , то
, то 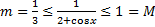 . По теореме об оценке
. По теореме об оценке 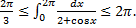
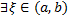 такая, что
такая, что  .
.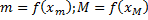 ,
, 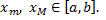 По теореме об оценке
По теореме об оценке 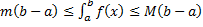 , (равенство возможно только для
, (равенство возможно только для  т.е. для непрерывных функций, отличных от константы
т.е. для непрерывных функций, отличных от константы 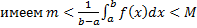 . По теореме о промежуточном значении непрерывной функции:
. По теореме о промежуточном значении непрерывной функции:  . Возьмем
. Возьмем 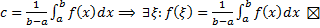 .
.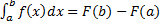 .
.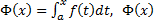 – также первообразная. Тогда
– также первообразная. Тогда  . Т.к.
. Т.к. 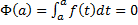 , то
, то 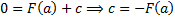 , т.е.
, т.е.  . При
. При  :
:  или
или 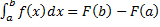 :
: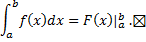
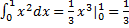 .
.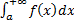 ,
,  сходятся, то сходятся интегралы
сходятся, то сходятся интегралы
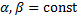 .
.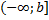 .
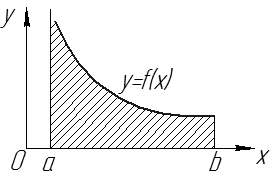
.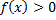 – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 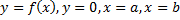 (см. рис. 15).
(см. рис. 15).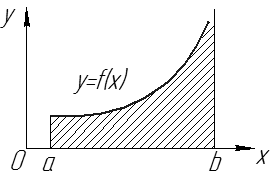
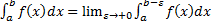 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 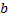 .
.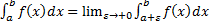 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 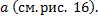
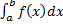 ,
, 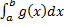 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы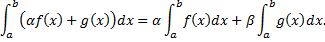
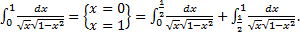
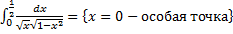 .
.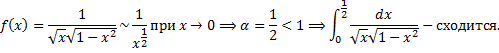
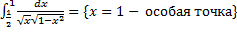 .
.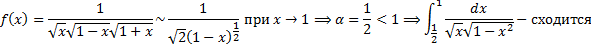
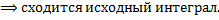
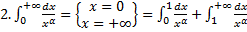 .
.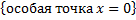 + несобственный интеграл 1-го рода
+ несобственный интеграл 1-го рода 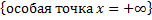 ).
).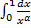 – сходится при
– сходится при 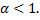
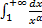 – сходится при
– сходится при 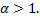
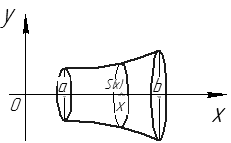
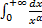 расходится для любого
расходится для любого 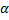 .
.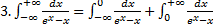 .
.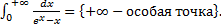
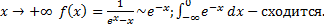
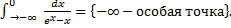
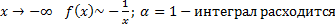 .
.
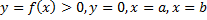 , вращается вокруг оси
, вращается вокруг оси 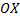 (см. рис. 26).
(см. рис. 26).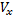 тела вращения. Зафиксируем
тела вращения. Зафиксируем 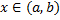 . Сечение тела плоскостью
. Сечение тела плоскостью 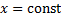 – круг радиуса
– круг радиуса 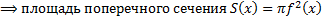 . Тогда
. Тогда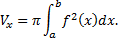
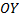 (см. рис. 27).
(см. рис. 27).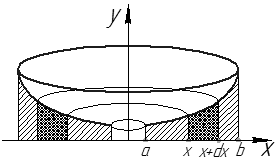
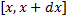 , где
, где 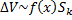 , где
, где 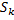 – площадь кольца радиусов
– площадь кольца радиусов 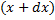 соответственно:
соответственно: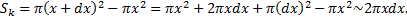
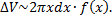
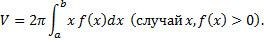
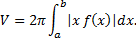
 , имеем
, имеем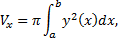
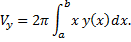
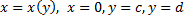 (см. рис. 28).
(см. рис. 28).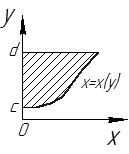
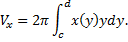
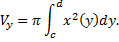
 задана параметрическими уравнениями:
задана параметрическими уравнениями:

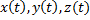 имеют на
имеют на  непрерывные производные.
непрерывные производные.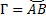 ,
, 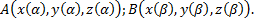

 – переменная дуга длиной
– переменная дуга длиной 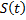 .
.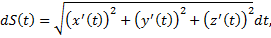
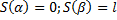 – длина всей дуги.
– длина всей дуги.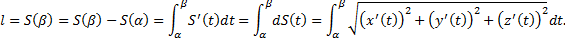
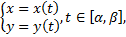

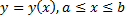 :
: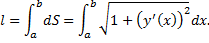
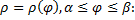
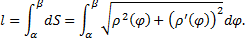


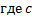 – произвольная положительная постоянная (см. рис. 30).
– произвольная положительная постоянная (см. рис. 30). :
: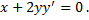
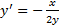 - ДУ семейства эллипсов. Тогда
- ДУ семейства эллипсов. Тогда  =
= 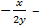
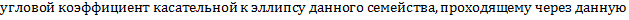
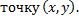
 угловой коэффициент касательной должен быть равен
угловой коэффициент касательной должен быть равен 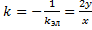 , т.е. ДУ ортогонального семейства:
, т.е. ДУ ортогонального семейства: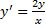 .
.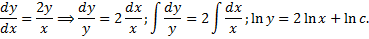
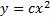 – семейство парабол.
– семейство парабол.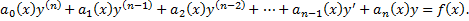
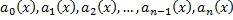 и правая часть
и правая часть  . Разделим на
. Разделим на 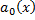 . Получим ДУ вида
. Получим ДУ вида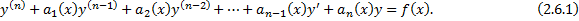
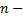 го порядка. Соответствующее ЛОДУ:
го порядка. Соответствующее ЛОДУ: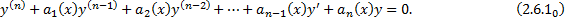

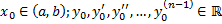 .
.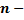 го порядка
го порядка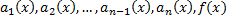 непрерывны на
непрерывны на 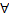 точки
точки 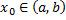 и
и 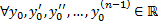
 решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале
решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале 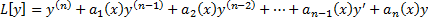 .
.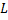 является линейным оператором, т.е.
является линейным оператором, т.е. 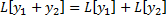 и
и 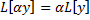 , где
, где 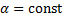 .
.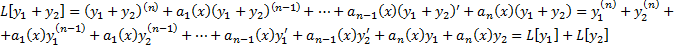 ,
,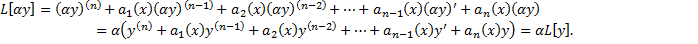
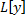 – линейный дифференциальный оператор.
– линейный дифференциальный оператор.

 . Рассмотрим СЛАУ относительно
. Рассмотрим СЛАУ относительно 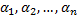 :
: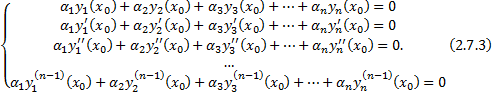
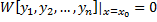 , следовательно, система имеет ненулевое решение, т.е.
, следовательно, система имеет ненулевое решение, т.е. 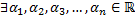 , не все равные
, не все равные  , такие, что выполняется система (2.7.3).
, такие, что выполняется система (2.7.3).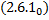 .
.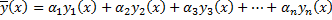 .
. начальным условиям (в силу (2.7.3)):
начальным условиям (в силу (2.7.3)):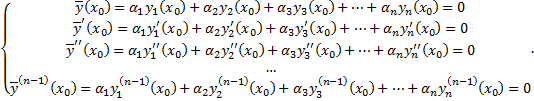
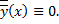
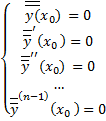 .
.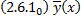 и
и  удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши
удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши 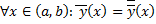 , т.е.
, т.е. 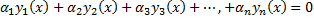 , т.е.
, т.е. 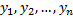 – линейно зависимы на
– линейно зависимы на 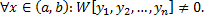
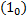 . График функции
. График функции  может иметь вид (см. рис. 37, 38):
может иметь вид (см. рис. 37, 38):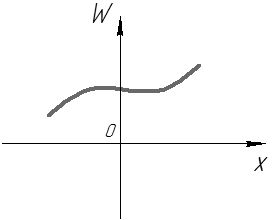 Рис. 37
Рис. 37
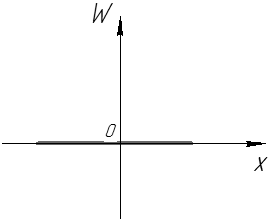 Рис. 38
Рис. 38
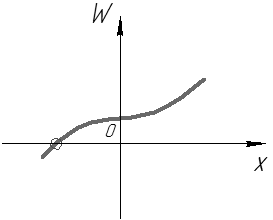 Рис. 39
Рис. 39
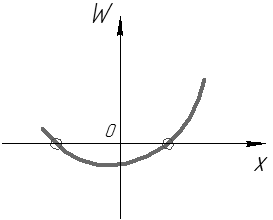 Рис. 40
Рис. 40


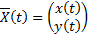 – частное решение автономной системы
– частное решение автономной системы  . Рассмотрим на плоскости
. Рассмотрим на плоскости  кривую
кривую  , заданную параметрическими уравнениями
, заданную параметрическими уравнениями
 на фазовой плоскости
на фазовой плоскости 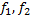 имеют непрерывные частные производные первого порядка в области
имеют непрерывные частные производные первого порядка в области 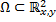 , то через каждую точку области
, то через каждую точку области 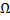 проходит ровно одна фазовая кривая.
проходит ровно одна фазовая кривая.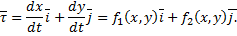
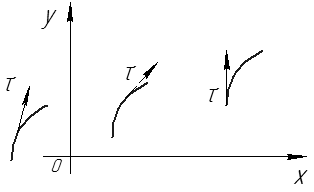
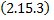 как функцию
как функцию 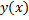 , заданную параметрически, тогда
, заданную параметрически, тогда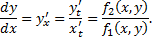
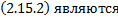 интегральными кривыми ДУ 1-го порядка
интегральными кривыми ДУ 1-го порядка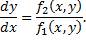
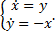
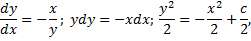
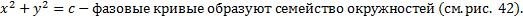



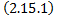 в области
в области 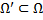 , если выполняется 2 условия:
, если выполняется 2 условия: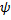 имеет непрерывные частные производные 1-го порядка в области
имеет непрерывные частные производные 1-го порядка в области 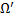 и для
и для 
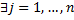 , что
, что 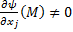 .
.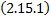
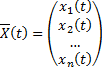

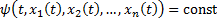 .
. 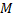
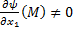 . Тогда по теореме о неявной функции из
. Тогда по теореме о неявной функции из 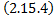 можно в некоторой окрестности т.
можно в некоторой окрестности т. 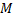 выразить
выразить 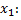
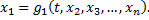
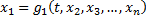 в уравнения системы
в уравнения системы 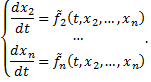
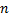 независимых первых интегралов:
независимых первых интегралов:
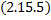 неявно задает решение системы.
неявно задает решение системы.
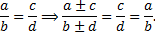


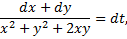


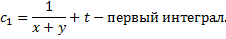

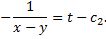
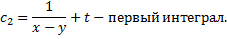

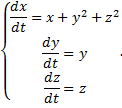



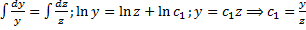 - (1-й интеграл).
- (1-й интеграл).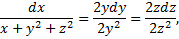
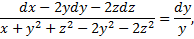
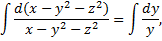
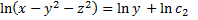 ,
,