
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классы эквивалентности, фактор-множество ⇐ ПредыдущаяСтр 5 из 5
Определение. Пусть ~ - произвольное отношение эквивалентности на множестве X и а Î X. Тогда классом
Классы эквивалентности обладают следующими свойствами: 1. Порождающий элемент а принадлежит классу 2. Если 3. Для любых элементов а, b Î X
Другими словами, классы эквивалентности совпадают, тогда и только тогда, когда их порождающие элементы эквивалентны. 4. Любые два класса эквивалентности либо равны, либо не имеют общих элементов. Это свойство, очевидно, равно сильно следующему: " a, b Î X ( 5. Множество X, на котором задано некоторое отношение эквивалентности, равно объединению всех классов этой эквивалентности, т.е.
Доказательство. Первое свойство, очевидно, следует из рефлексивности отношения ~. Свойство 2. Пусть Пусть Обратно, пусть Свойство 3. Импликация Обратно, если а ~ b, то Свойство 4. Пусть Из принадлежности Свойство 5. Из свойства 1 следует, что каждый элемент множества X содержится в некотором классе эквивалентности. Это означает, что С другой стороны, очевидно, что 1) все подмножества (классы) 2) любые два различных подмножества 3) объединение всех таких подмножеств есть множество X, т.е. Например, множество А = {1,2,3,4,5} можно разбить на классы
Следующая теорема указывает на важную связь между понятиями "эквивалентность" и "разбиение". Теорема 3. Классы любой эквивалентности на множестве X образуют разбиение этого множества. Обратно, для каждого разбиения на множестве можно определить эквивалентность на этом множестве так, что ее классы образуют исходное разбиение. Доказательство. I. Пусть на множестве X задана эквивалентность ~. Покажем, что все различные классы этой эквивалентности образуют разбиение множества X. Действительно, свойство 1) разбиения вытекает из свойства 1 классов эквивалентности. Свойство 2) разбиения выполняется ввиду свойства 4 дляклассов эквивалентности. И, наконец, свойство 3) разбиения имеет место в силу свойства 5 для классов эквивалентности. Итак, первое утверждение теоремы доказано. Обратно, пусть на множестве X задано разбиение, т. е семейство Определим на множестве X бинарное отношение F поправилу: х Fу тогда и только тогда, когда элементы принадлежат одному и тому же подмножеству данного разбиение Другими словами, Легко проверяется, что отношение F является эквивалентностью. Покажем теперь, что классы этой эквивалентности есть в точности подмножества данного разбиения. Пусть Обратно, пусть Отсюда, поскольку по определению разбиения каждый элемент множества X принадлежит только одному подмножеству разбиения и Обратно, взяв произвольное подмножество
Теорема доказана. Определение. Фактор - множеством множества X по отношению эквивалентности F называется множество, каждый элемент которого является одним из классов эквивалентности. Обозначается фактор - множество символом Х / F. Пример. Пусть
Тогда фактор - множество Х/ F можно рассматривать как множество рациональных чисел. При этом рациональное число определяется как класс эквивалентности
Рассмотрим конечное множество
Приведенная таблица устанавливает соответствие между элементами множества А. В верхней строке ее записаны элементы множества А, а под каждым из них в нижней строке находится его образ. В этом случае говорят, что на множестве А задана унарная операция. В алгебре часто изучаются операции, связывающие пары чисел с третьим числом. Такие операции называются бинарными. Примерами бинарных операций являются: сложение, умножение на множестве R действительных чисел и другие. Определение 1. Бинарной операцией на множестве А называется произвольное отображение
Таким образом, бинарная операция каждой упорядоченной паре (а, b) элементов множества А ставит в соответствия третий элемент с этого же множества, а именно, образ пары
и читают: "элемент с есть результат операции Т над элементами а и b". Вместо символа Г часто используется один из знаков " + " (сложение) или " × " (умножение). В первом случае говорят об использовании аддитивной терминологий, во втором - мультипликативной. Результат операции называется, соответственно, суммой или произведением. Примеры: 1. Сложение и умножение на каждом из множеств N, Z, Q, R, где N, Z, Q, R обозначают, соответственно, множество натуральных, целых, рациональных и действительных чисел. 2. Возведение в степень на множестве натуральных чисел. 3. Объединение и пересечение на множестве подмножеств некоторого множества. Контрпримеры: 1. Вычитание на множестве N не является бинарной операцией, т.к. при вычитании из меньшего числа большего получаем число, не принадлежащее множеству N. 2. Умножение во множестве иррациональных чисел Ω = R \ Q также не является бинарной операцией, т.к., например, Пусть Е - множество с бинарной операцией Т и F Í Е. Тогда, если результат операции над любыми двумя элементами из F также принадлежит F, то множество F называется замкнутым относительно рассматриваемой операции Т. Например, множество По аналогии с понятием п - арного отношения (гл.II,§6) можно обобщить определение операции на любое число аргументов: пусть А- множество и п - фиксированное натуральное число. Тогда п - арной операцией на множестве А называется произвольное отображение
Таким образом, всякая п - арная операция Т произвольному упорядоченному набору Очевидно, что при п = 1 операция Т становится унарной, а при п = 2 - бинарной. Используется также термин 0 - арная операция. Говорят, что на множестве определена 0 –арная операция, если на этом множестве зафиксирован некоторый элемент е. Заметим, что вместо фразы " Т является п -арной операцией "иногда говорят, что "арность операции Т равна n ".
Аналогичное соглашение имеет место и для п - арных отношений. Свойства бинарной операции Ассоциативность. Бинарная операция Т называется ассоциативной, если Например, сложение и умножение во множестве натуральных чисел N ассоциативно, а возведение в степень - не ассоциативно, поскольку равенство Коммутативность. Бинарная операция T называется коммутативной, если
для любых а, b Î А. Регулярный элемент. Элемент а называется регулярным относительно бинарной операции T, если для любых x, y Î А, равенства аТх = аТу и хТа = уТа влекут х = y. В этом случае говорят, что равенства можно сократить на a. Примеры: 1. Относительно сложения во множестве действительных чисел R любое число регулярно. 2. Относительно умножения во множестве R регулярным является всякое число, кроме нуля, так, например, 0×2 = 0×7, но 2 ¹7. Нейтральный элемент. Пусть А - множество с бинарной операцией Т. Нейтральным элементом относительно операции Т называют такой элемент е Î А, что равенство еТх = хТе = х справедливо для любого х Î А. Легко проверить, что если такой элемент существует, то он единственен. Нейтральный элемент, как видно из определения, регулярен. Как правило, в аддитивной терминологии нейтральный элемент называют нулем, а в мультипликативной - единицей. Например, во множестве целых чисел Z нейтральным элементом относительно сложения является число 0, а число 1 служит нейтральным элементом относительно умножения. Во множестве Р(А) всех подмножеств данного множества А пустое множество Æ выполняет роль нейтрального элемента относительно операции объединения.
Симметричные элементы. Пусть бинарная операция Т задана на множестве А, обладает нейтральным элементом е. Говорят, что элемент
В аддитивной терминологии симметричный элемент называется противоположным, а в мультипликативной - обратным к данному. Примеры: 1. Если а Î R, то число - а Î R, является симметричным (противоположным) элементом относительно сложения. 2. Если а Î R и а ¹ 0, то число 3. Если е - нейтральный элемент, то его симметричным элементом служит он сам, т.к. Из равенств (1) очевидным образом следует, что если элемент Следствие 1. Пусть А - множество с ассоциативной бинарной операцией Т и нейтральным элементом е. Тогда любой элемент а Î А не может иметь более одного симметричного элемента. Доказательство. Пусть
Дистрибутивность. Пусть на множестве А определены две бинарные операции Т и ^. Говорят, что операция Т дистрибутивна относительно операции ^, если для любых а, b, с имеет место
Примеры: 1. На множестве действительных чисел R умножение дистрибутивно относительно сложения:
Однако сложение не дистрибутивно относительно умножения. 2. Для операций объединения и пересечения подмножеств произвольного универсального множества справедливы равенства:
Следовательно, каждая из этих операций дистрибутивна относительно другой. § 12. Понятие об алгебраической системе. Алгебры и модели. Классические примеры алгебр. Изоморфизм алгебр Пусть А - произвольное множество. В дальнейшем это множество будем называть основным или носителем (построенной) алгебраической системы. Зафиксируем на носителе А некоторые операции Пусть Определение. Тройка множеств Сигнатура алгебраической системы может быть и бесконечной (условие конечности в приведенном выше определении выбрано ради краткости). Алгебраическая система - это множество (носитель) с набором (возможно бесконечным) операций и отношений, определенных на этом множестве. Алгебраическая система называется алгеброй, если предикатная часть ее сигнатуры является пустым множеством (
Если же функциональная часть сигнатуры алгебраической системы пуста, т.е. Отметим, что создателем теории алгебраических систем является выдающийся советский математик А. И. Мальцев (1909 - 1967). Читатель, желающий познакомиться с основными идеями этой теории, может обратиться к книге [10]. Примеры: Пусть символы Тогда следующие три алгебраические системы
являются алгебрами. Первые две из них имеют тип Алгебраическая система Алгебраическая система Другие примеры будут приведены ниже.
1. Алгебра с одной бинарной операцией называется группоидом. Например, каждое из множеств N, Z, Q, R образует группоид относительно операции сложения либо умножения. 2. Алгебра с одной бинарной ассоциативной операцией называется полугруппой. Очевидно, все группоиды, указанные в предыдущем пункте, являются полугруппами. Однако в общем случае это утверждение не верно, т.е. класс группоидов более широк, чем класс полугрупп. Например, целые числа относительно операции вычитания образуют неассоциативный группоид. Приведем другой пример группоида, который не является полугруппой. Пусть А = {а, b} - двухэлементное множество. Зададим операцию Т на множестве А следующими равенствами:
Тогда Следовательно, операция Т неассоциативна. Это означает, что группоид Заметим, что операции T, построенной в предыдущем примере, соответствует следующая таблица:
Такие таблицы называются таблицами Кэли. Они используются, как правило, для задания бинарной операции на конечном множестве и устроены следующим образом. Элементы носителя А записывают в верхней строке и в левом вертикальном столбце. Далее для каждой упорядоченной пары В теории полугрупп важнейшую роль играют так называемые "полугруппы отображений множеств (в себя)". Устроены они так: Пусть А - произвольное фиксированное множество. В качестве носителя полугруппы выбирается множество М(А), состоящее из всех отображений множества А в себя:
Операцией на множестве М(А) служит композиция отображений (гл. II, § 5). Очевидно, что для любых f, g Î М(А) их композиция Таким образом, 3. Полугруппа Позже будет показано, что это определение "избыточно", т.е. можно некоторые требования в определении ослабить. С этой целью сформулируем определение группы в мультипликативной терминологии. Группоид 1. 2. 3.
Аналогичное утверждение имеет место и для элемента, обратного к любому данному. В связи с этим элемент, обратный к элементу а, имеет стандартное обозначение Таким образом, последнее определение группы равносильно исходному, но оно содержит "меньше" требований (требуется наличие только правой единицы, и для каждого элемента - существование только правого обратного). Для перевода определения группы на аддитивный язык достаточно: знак умножения (×) заменить знаком сложения (+), слова "произведение", "единица" и "обратный", соответственно, - словами "сумма", "нуль" и "противоположный". Аксиомы 1-3 будут выглядеть так:
Элемент, противоположный элементу а, обозначается через (- а). Группа
Для абелевых групп, как правило, используется аддитивная терминология. Примеры: Каждое из множеств Z, Q и R образует группу относительно операции сложения. Однако, натуральные числа не образуют ни по сложению ни по умножению. Очевидно также, что если в качестве носителя выбрать одно из множеств Важнейший класс в теории групп образуют так называемые "группы преобразований" или "группы подстановок". Преобразованием множества А называется любое биективное отображение множества А на себя. Зафиксируем множество А, и через S(А) обозначим множество всех биекций
Тогда нетрудно показать, что композиция любых двух отображений f, g из S(А) снова является биекцией (см., напр., упр. 12, с. 47) и, следовательно, Действительно, ассоциативность операции вытекает из теоремы 1 (гл.II, §5). В этой же теореме содержится утверждение о том, что тождественное отображение Проверим выполнимость третьей аксиомы. Пусть Тогда по признаку обратимости отображения существует отображение Таким образом, и третья аксиома выполняется и, значит, Если А - конечное множество, то вместо термина "преобразование" используется его синоним "подстановка". В этом случае, если множество А содержит п элементов, то вместо S (А) используется запись
Пусть Определение. Группоид
Биекцию в этом случае называют отображением, осуществляющим изоморфизм данных группоидов. Заметим, что условие (*) в словесной формулировке часто выражают словами: "отображение сохраняет групповую операцию Т ". Из определения очевидным образом следует, что отношение изоморфизма между группами обладает свойствами рефлексивности, симметричности и транзитивности. Запись G L означает, что группоид Нетрудно проверить, что в этом случае, если Примеры: 1. Пусть G = Z и Т - сложение. Ранее уже отмечалось, что Пусть Легко проверить, что Пусть Покажем, что f осуществляет изоморфизм Z L. Действительно, если
Следовательно, f - инъективно. Сюрьективность отображения f очевидна, и, значит, f - биекция. Проверим теперь, что отображение f удовлетворяет условию (*). Пусть 2. Нетрудно проверить, что отображение Действительно, биективность очевидна, а условие (*) выполняется в силу равенства Понятие изоморфизма играет фундаментальную роль в математике. Из определения следует непосредственно, что изоморфные группоиды имеют одинаковое количество элементов. Читатель без особого труда докажет, что "единица группы при изоморфизме переходит (отображается) в единицу другой группы, элемент, обратный к данному, - в обратный к его образу" и т.д. Несколько больших усилий требуется для понимания и доказательства следующего (более общего) утверждения: "Если некоторая формула исчисления предикатов истинна на одной из изоморфных между собой группах, то она истинна и на другой". Другими словами, изоморфные группы имеют одинаковые алгебраические свойства (т.е. свойства, сформулированные в общелогических терминах и терминах операций, с помощью которых заданы данные группы). Это замечание справедливо и для любых алгебр, изоморфных между собой. Однако понятие изоморфизма для произвольных алгебр нами еще не дано. Приведем его. Заметим, что если результат бинарной операции Т над элементами
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 1274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.48.62 (0.143 с.) |
 эквивалентности ~ с порождающим элементом а называется множество всех элементов x Î X, эквивалентных элементу а, т.е.
эквивалентности ~ с порождающим элементом а называется множество всех элементов x Î X, эквивалентных элементу а, т.е.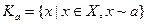 .
.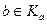 , то
, то 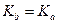 т. е. любой элемент из класса эквивалентности может быть выбран в качестве порождающего элемента.
т. е. любой элемент из класса эквивалентности может быть выбран в качестве порождающего элемента. .
.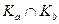 ¹ Æ ®
¹ Æ ® 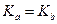
 ).
).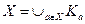 .
.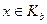 Тогда x ~ b. В то же время из
Тогда x ~ b. В то же время из 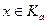 . Этим доказано включение
. Этим доказано включение 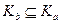 .
.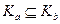 . Следовательно,
. Следовательно, 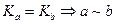 очевидна ввиду свойства 2.
очевидна ввиду свойства 2.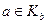 , откуда по свойству 2 вытекает равенство
, откуда по свойству 2 вытекает равенство 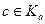 и
и 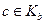 одновременно.
одновременно.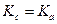 . Аналогично из
. Аналогично из  . Следовательно,
. Следовательно,  .
.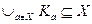 , поскольку каждый класс
, поскольку каждый класс  подмножеств
подмножеств 



 образует разбиение этого множества на классы
образует разбиение этого множества на классы  если:
если: не пересекаются (т.е.
не пересекаются (т.е. 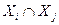 ¹ Æ);
¹ Æ);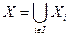 .
.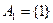 ,
, 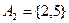 ,
,  ; множество целых чисел Z можно разбить на классы нечетных чисел
; множество целых чисел Z можно разбить на классы нечетных чисел 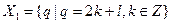 и четных чисел
и четных чисел 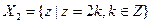 .
. .
. данного разбиения такое, что
данного разбиения такое, что 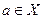 . Это означает, что любой элемент
. Это означает, что любой элемент 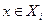 находится в отношении F с элементом а и, значит,
находится в отношении F с элементом а и, значит, 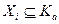 .
.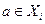 , то
, то 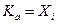 . Таким образом, показано, что каждый класс эквивалентности F совпадает с некоторым подмножеством данного разбиения.
. Таким образом, показано, что каждый класс эквивалентности F совпадает с некоторым подмножеством данного разбиения.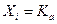 .
.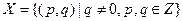 . Отношение на множестве X определим по правилу:
. Отношение на множестве X определим по правилу: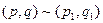 , тогда и только тогда, если
, тогда и только тогда, если  .
. , т.е. семейство
, т.е. семейство 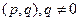 , где при
, где при 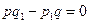 две пары
две пары  и
и 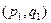 определяют одно и то же рациональное число.
определяют одно и то же рациональное число.
 § 11. Операции на множестве
§ 11. Операции на множестве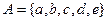 и зададим отображение множества А в А с помощью следующей таблицы:
и зададим отображение множества А в А с помощью следующей таблицы:  .
.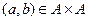 при отображении T, т.е.
при отображении T, т.е. 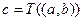 . В практике последняя запись встречается редко. Как правило, вместо нее пишут:
. В практике последняя запись встречается редко. Как правило, вместо нее пишут:
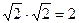 и число 2 ¹ Ω.
и число 2 ¹ Ω.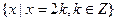 четных целых чисел является замкнутым подмножеством относительно сложения и умножения на множестве Z, а множество иррациональных чисел Ω Í R не является замкнутым подмножеством относительно операции умножения на множестве R.
четных целых чисел является замкнутым подмножеством относительно сложения и умножения на множестве Z, а множество иррациональных чисел Ω Í R не является замкнутым подмножеством относительно операции умножения на множестве R.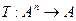 (
(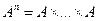 - декартово произведение п сомножителей, равных А).
- декартово произведение п сомножителей, равных А). из п элементов данного множества А ставит в соответствие единственный элемент
из п элементов данного множества А ставит в соответствие единственный элемент 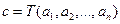 этого множества.
этого множества.
 Например, арность любой бинарной операции равна 2, унарной - 1 и т.д.
Например, арность любой бинарной операции равна 2, унарной - 1 и т.д. для любых элементов а, b, с Î A.
для любых элементов а, b, с Î A. выполняется не для всех натуральных чисел. Например,
выполняется не для всех натуральных чисел. Например, 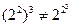 .
.
 симметричен элементу а Î А, если
симметричен элементу а Î А, если . (1)
. (1)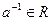 является симметричным (обратным) элементом относительно умножения.
является симметричным (обратным) элементом относительно умножения. .
. , т.е.
, т.е.  .
.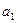 и
и 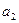 - симметричные к а элементы относительно бинарной операции Т. По определению, имеем
- симметричные к а элементы относительно бинарной операции Т. По определению, имеем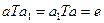 ; (2)
; (2)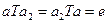 . (3)
. (3)

 Тогда, очевидно,
Тогда, очевидно, 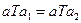 , откуда
, откуда 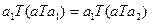 . Отсюда, в силу ассоциативности операции Т, получим
. Отсюда, в силу ассоциативности операции Т, получим 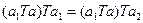 Теперь из (2) следует, что
Теперь из (2) следует, что  и, значит,
и, значит, 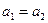 .
. .
.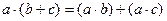 .
.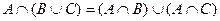 ;
;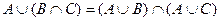 .
. . и отношения (предикаты)
. и отношения (предикаты)  .
. - арность операции
- арность операции 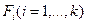 и
и 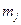 - арность отношения
- арность отношения  . Положим далее
. Положим далее 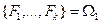 и
и 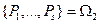 .
. называется алгебраической системой типа
называется алгебраической системой типа  . Множество
. Множество 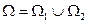 , состоящее из символов операций
, состоящее из символов операций  называют функциональной,
называют функциональной, 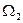 - предикатной частью сигнатуры данной системы.
- предикатной частью сигнатуры данной системы. и
и 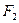 обозначают, соответственно, операции сложения и умножения на множестве N натуральных чисел, а Р- отношение ≤ ("меньше либо равно").
обозначают, соответственно, операции сложения и умножения на множестве N натуральных чисел, а Р- отношение ≤ ("меньше либо равно").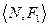 ,
,  ,
, 
 , а тип третьей равен
, а тип третьей равен 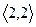 .
.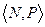 является моделью.
является моделью. имеет тип
имеет тип  , Она не является ни алгеброй, ни моделью.
, Она не является ни алгеброй, ни моделью.


 Классические алгебры
Классические алгебры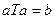 ,
, 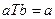 ,
, 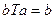 ,
, 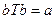 .
.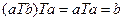 . В то же время
. В то же время 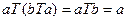 , и, значит,
, и, значит, 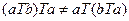 .
. не является полугруппой.
не является полугруппой. результат
результат 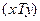 помещается в клетку, стоящую на пересечении строки, содержащей элемент х, и столбца, содержащего элемент у.
помещается в клетку, стоящую на пересечении строки, содержащей элемент х, и столбца, содержащего элемент у.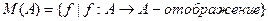 .
.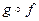 также является отображением множества А в себя и, следовательно,
также является отображением множества А в себя и, следовательно,  . Ассоциативность операции о композиции гарантируется теоремой 1 (гл.II, §5).
. Ассоциативность операции о композиции гарантируется теоремой 1 (гл.II, §5).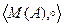 - полугруппа для любого множества А.
- полугруппа для любого множества А. называется группой, если она имеет нейтральный элемент, относительно которого любой элемент a Î G имеет симметричный элемент.
называется группой, если она имеет нейтральный элемент, относительно которого любой элемент a Î G имеет симметричный элемент.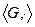 с операцией × умножения называется группой, если выполнены следующие условия:
с операцией × умножения называется группой, если выполнены следующие условия: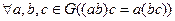 (ассоциативность операции умножения);
(ассоциативность операции умножения); (элемент е называют при этом правой единицей);
(элемент е называют при этом правой единицей);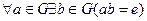 (элемент b называется правым обратным для а).
(элемент b называется правым обратным для а).






 Условия 1-3 называют аксиомами группы. Опираясь на них, можно доказать, что в группе существует только одна единица е, которая является одновременно и правой, и левой. Никаких других единиц ни правых, ни левых не существует.
Условия 1-3 называют аксиомами группы. Опираясь на них, можно доказать, что в группе существует только одна единица е, которая является одновременно и правой, и левой. Никаких других единиц ни правых, ни левых не существует.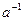 .
.
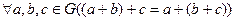 ;
;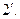
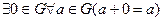 ;
;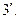
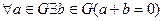 .
.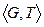 называется коммутативной, либо абелевой,-, если групповая операция Т коммутативна, т. е.
называется коммутативной, либо абелевой,-, если групповая операция Т коммутативна, т. е.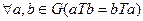
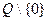 ,
, 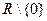 ,
,  ,
, 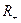 , где
, где  ,
,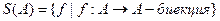 .
. . Таким образом, композиция является бинарной операцией на множестве S(А). Теперь уже легко установить, что алгебра
. Таким образом, композиция является бинарной операцией на множестве S(А). Теперь уже легко установить, что алгебра 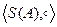 является группой.
является группой.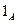 множества А играет роль единицы при композиции отображений. Следовательно, композиция удовлетворяет аксиомам 1 и 2.
множества А играет роль единицы при композиции отображений. Следовательно, композиция удовлетворяет аксиомам 1 и 2.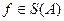 , тогда
, тогда 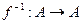 , обратное к f, т.е
, обратное к f, т.е  , Это означает, что
, Это означает, что 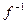 - обратимо. Отсюда снова по той же теореме 2 получим, что
- обратимо. Отсюда снова по той же теореме 2 получим, что 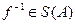 .
. .
.





 Группа
Группа 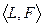 - группоиды.
- группоиды.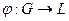 такая, что
такая, что (*)
(*)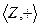 - группа.
- группа.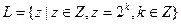 и F - умножение (на множестве L).
и F - умножение (на множестве L). отображение, определяемое по правилу:
отображение, определяемое по правилу: 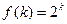 для любого k Î2.
для любого k Î2.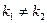 , то одно из этих чисел меньше другого. Пусть, например,
, то одно из этих чисел меньше другого. Пусть, например, 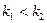 . Тогда, поскольку f - возрастающая функция, то
. Тогда, поскольку f - возрастающая функция, то  , т.е.
, т.е.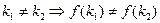 .
.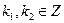 . Тогда
. Тогда 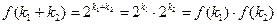 . Утверждение доказано.
. Утверждение доказано.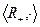 является группой относительно операции умножения.
является группой относительно операции умножения.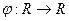 , определенное по правилу
, определенное по правилу  для любого
для любого 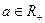 , осуществляет изоморфизм между группой
, осуществляет изоморфизм между группой 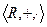 .
.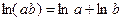 для любых
для любых 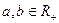 (т.е.
(т.е. 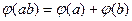 ).
).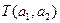 , то усл
, то усл


