
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соответствия, отображения (функции),
БИНАРНЫЕ ОТНОШЕНИЯ И ОПЕРАЦИИ Соответствие Пусть A, В-множества. Соответствием из A в В называется произвольное подмножество Fдекартова произведения При этом множество Aназывается областью отправления соответствия F, а B-его областью прибытия. Таким образом, всякое соответствие определяется тройкой множеств < F, A, B>, где Два соответствия < F, A, B> и Если (а, b) Таким образом, множество F можно рассматривать как некоторое множество стрелок, начало которых принадлежит области отправления соответствия, а конец - области прибытия. Если множества А и В зафиксированы, то для задания соответствия из A в В достаточно определить множество F. Для этого следует указать правило, позволяющее для каждого элемента а
1. Пусть А = {1,2,3},В = {a, b}, F ={(1,a),(2,a),(2,b)} 2. Пусть А, Втакие же, как и в предыдущем пункте. Тогда то же множество F может быть указано как множество стрелок (рис. 3). 3. Пусть А = В = N - множество положительных целых чисел. Множество Fесть область истинности предиката " х - делитель у ", т.е. F= {(x, у) \ x - делитель у}.
 §2. Отображение (функция) §2. Отображение (функция)
В общей ситуации не каждый элемент из области отправления соответствия обязан иметь образ или, напротив, он может иметь более одного образа. Если каждый элемент области отправления соответствия имеет единственный образ, то такое соответствие называется отображением, или функцией. Для отображений принята специальная терминология: область отправления именуется областью определения; а область прибытия - областью значений. Подчеркнем, что отображение f: X ® Y определено лишь в том случае, когда каждый элемент х Î X имеет во множестве Y единственный образ у ÎY. Это обстоятельство записывается в виде равенства y = f(x), которое обозначает, что "элемент у есть образ элемента х при отображении f " или "элемент х есть прообраз элемента у при отображении f ". Отметим, что в общем случае для соответствия F использование равенства у = F (х) может привести к противоречию.
Например, если при соответствии F: X ® Y элемент x Î X имеет два различных образа Если множество G Í X, то через f(G) обозначается множество образов всех элементов множества G:
Множество f(G)называется образом множества G при отображении f. Пример. Пусть отображение f:R®R определяется как § 3. Сужение отображения. График. Последовательность Пусть имеем отображение f: X ® Y, и пусть G Í X. Тогда отображение f всякому элементу из G ставит в соответствие некоторый элемент из Y, стало быть, оно определяет отображение Отображение
П р и м е р 1. Отображение Множество пар { x, f(x) }, являющееся подмножеством произведения Х ´ Y, называется графиком функции f(x) (рис. 5).
П р и м е р 2. Множество пар 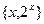 являющееся подмножеством произведения являющееся подмножеством произведения 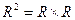 , составляет график; показательной функции , составляет график; показательной функции 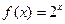 (рис. 6). (рис. 6).
Возьмем N - множество натуральных чисел, в качестве Y -произвольное множество. Отображение f: N ®Y называется последовательностью элементов из Y. Таким образом, последовательность f связывает каждое натуральное число п с некоторым элементом Последовательность f будем обозначать § 4. Типы отображений Пусть f: X ® Y - отображение. Тогда каждому элементу х Î X соответствует единственный элемент у Î Y, с другой стороны, элемент у Î Y может быть образом нескольких элементов из X. Например, значение -6 служит для функции
Пусть В Í Y, Тогда через
1. Отображение f: X ® Y называется сюръективным, или сюръекцией, или отображением, на множество Y, если каждый элемент у Î Y из области его значений имеет хотя бы один прообраз, т.е. множество
Очевидно, что отображение f: X ® Y является сюръекцией тогда и только тогда, когда f(X) = Y. Заметим, что в этом утверждении равенство f(X) = Y можно заменить равносильным ему равенством: Примеры: а) Пусть X = У = R. Отображение f, определяемое формулой б) Пусть X = У = R. Отображение f, определяемое формулой
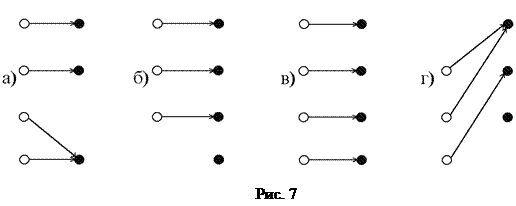
2. Говорят, что отображение f: X ® Y является взаимнооднозначным или инъективным, если образы любых двух различных элементов 3. Отображение f: X ® Y называют биективным или биекцией, если оно одновременно инъективно и сюръективно, т.е. если каждый элемент Y является образом некоторого единственного элемента из X. Примеры: Отображение, заданное на рисунках: 7 а) - сюръективно, но не инъективно; 7 б) - инъективно, но не является сюръекцией; 7 в) - биекция;
7 г) - не обладает ни одним из указанных свойств. Отображение f: X ® Y, определенное равенством f(x) = х, называется тождественным, и обозначается: § 5. Композиция отображений, обратимые отображения Пусть X, Y, Z - множества f: X ® Y и g: Y ® Z - отображения. Отображение h: X ® Z, определяемое формулой h(x) = g(f(x)) называется композицией, или суперпозицией, или произведением отображений f и g и обозначается через В том случае, когда f и g именуются функциями, Теорема 1. Композиция отображений обладает следующими свойствами: 1) если f: X ® Y, g: Y ® Z и h: Z ® W - отображения, то 2) для любого отображения f: X ® Y имеют место равенства Пусть f: X ® Y, g: Y ® Z и h: Z ® W, т.е.
т.е. Пусть f: X ® Y - отображение. Тогда Замечание. Композиция отображений в общем случае не обладает коммутативностью, существуют отображения f и j, что произведения Например, пусть f: R ® R, Отображение f: A ® B называется обратимым, если существует отображение j: B ® A такое, что
Отображение j, удовлетворяющее равенства (*), называется обратным к отображению f. Критерием обратимости отображения служит теорема 2 Теорема 2. Отображение обратимо тогда и только тогда, когда оно биективно. Необходимость. Пусть f: A ® B - обратимое отображение. Тогда, по определению, существует отображение j: B ® Aтакое, что выполняются оба равенства (*).
Покажем, что отображение f сюръективно. Пусть Докажем инъективностъ отображения f. Пусть Достаточность. Пусть f: A ® B - биективное отображение. Тогда ввиду сюръективности отображения f
В силу инъективности f для любого элемента В силу этого в дальнейшем для любого биективного отображения f под символом Тогда соответствие j из В в А, при котором образом произвольного элемента Теперь для доказательства обратимости отображения f достаточно проверить справедливость равенств (*). 1 Пусть а Î А. Тогда
т.е. 2. Далее, пусть Теорема доказана. Следствие. Если отображение f: A ® B обратимо, то оно имеет единственное обратное к нему отображение. Доказательство. Пусть отображение f: A ® B- обратимо. Тогда, в силу теоремы 2, отображение f - биективно. Обозначим через для любого Пусть Используя эти равенства и ассоциативность композиции отображений (теорема 1), получим
для произвольного Таким образом, если f биективно, то через Напомним, что для любого элемента
является определяющим для отображения Упражнения: 1. Пусть f: X ® Y - отображение. Докажите справедливость следующих импликаций:
(b) C Í D ® 2. Пусть f: X ® Y - отображение, A и В - произвольные подмножества множества X. Докажите справедливость следующих соотношений:
(а) (b) (c) 3. f: X ® Y – инъекция, А Í В Í X. Докажите, что 4. Пусть f: X ® Y – отображение, С и D – произвольные подмножества множества Y. Докажите справедливость следующих равенств: (a) (b) (c) 5. Пусть f: X ® Y – отображение. Доказать равносильность следующих утверждений: (а) f - сюръективно; (Ь) f(A) = В; (с) 6. Пусть
Найти композиции 7. Пусть A = {1, 2, 3, 4},
Построить 8. Пусть f: A → B – отображение. Докажите, что f является биекцией тогда и только тогда, когда множество 9. Докажите, что отображение f: A → B инъективно тогда и только тогда, когда для любого элемента b Î B множество 10. Какие из отображений, указанных в упражнении 6, сюръ-ективны, инъективны, биективны? 11. Докажите, что всякая возрастающая (убывающая) функция действительного переменного является инъекцией. 12. Два отображения называются однотипными, если оба они одновременно инъективны, сюръективны, либо биективны. Докажите, что композиция двух однотипных отображений является отображением того же типа. 13.Докажите, что если отображение f обратимо, то обратное к нему отображение 14. Докажите, что если композиция 15. Пусть f и g - обратимые отображения. Докажите, что если их композиция
В математике мы часто используем термины, которые характеризуют некоторые связи между парами объектов в определенном порядке. Например, "меньше", "включается", "делится на ", "параллельно" и т. д. Ниже мы увидим, что каждый из этих терминов является конкретизацией более широкого - "бинарное отношение". Для того, чтобы увидеть подходы к определению этого понятия, обратимся сначала к примеру. Пусть А = {1,2,6}. Тогда свойство "меньше" выделяет в декартовом квадрате А2 подмножество S = {(1,2), (1,6), (2,6)}, состоящее из тех и только тех пар чисел, у которых первое число меньше второго. Аналогично подмножество F = {(1,1),(2,2),(6,6),(1,2),(1,6),(2,6)} (4) характеризует свойство "делимости" чисел на множестве A. А именно, число х делит у тогда и только тогда, когда (x, y) Î F. Таким образом, если множество Fизвестно заранее, то для положительного ответа на вопрос "является ли число делителем b?" достаточно убедиться в том, что (а, b) Î F. Этим рассуждением мы вплотную приблизились к понятию бинарного отношения. Определение. Любое подмножество S Î А2 декартова квадрата множества А называется бинарным отношением определенным на множестве А. Из определения соответствия вытекает, что бинарное отношение на множестве А может быть определено как соответствие из А в А. Если пара (x, у) Î S, где x, у Î А, то говорят, что элементы х и у находятся в отношении S. Вместо записи (x, у) Î S используется также х Sу или S(x,у).
Отметим некоторые наиболее распространенные способу задания бинарных отношений: 1) Бинарное отношение может быть задано перечислением его элементов. Например, как уже отмечалось, множество F, заданное равенством (*), определяет бинарное отношение "делимости" на множестве А == {1, 2, 6}. 2) Бинарное отношение можно рассматривать как область истинности двухместного предиката. Например, отношение F, о котором говорится в пункте 1), совпадает с областью истинности предиката Р(х,у): " x делит у". 3) Бинарное отношение как частный случай соответствия Например, отношение F, определенное равенством (*), может быть задано следующим образом:
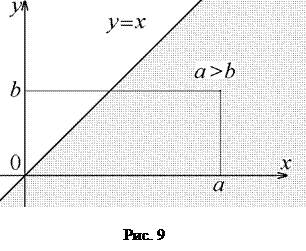
Такой рисунок часто называют диаграммой или графом отношения F. Диаграмма бинарного отношения F состоит из точек, изображающих основное множество А и стрелок, соединяющих их. При этом стрелка с началом x и концом у присутствует в диаграмме тогда и только тогда, когда (х, у) Î F. Диаграмма чаще всего используется для задания бинарных отношений на конечных множествах. 3) В случае, когда бинарное отношение задается на множестве действительных чисел R, множество принадлежащих ему пар может быть изображено точками плоскости. Это дает геометрическую иллюстрацию соответствующего отношения. Например, множество пар (x, у), для которых выполняется x > y, представляет множество точек плоскости, лежащих под прямой y = x (см. рис. 9).
Подмножество 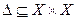 , составленное из всех пар равных между собой элементов, называется диагональю множества , составленное из всех пар равных между собой элементов, называется диагональю множества 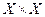 , т.е. , т.е.
Из определения вытекает, что отношение S(x, x), определяемое множеством D, является равенством. В предыдущем примере (рис. 9) диагональю D множества S´S будет множество точек прямой у = х. Заметим, что понятие бинарного отношения может быть распространено на более общую ситуацию. Для этого достаточно в определении бинарного отношения заменить слова "декартов квадрат" словами "декартова степень". Определение. Пусть А - множество и п - произвольное натуральное число. Тогда любое подмножество В частности, при n = 2 получаем определение бинарного отношения. При n = 1 отношение называется унарным. Отметим далее, что в математических рассуждениях слова п-арное отношение и п-местный предикат часто используются как синонимы. Проиллюстрируем эту связь для случая п = 2. Как мы уже отмечали, область истинности любого двухместного предиката Р(х, у) является бинарным отношением. Обратно, если S - бинарное отношение на множестве А, т.е. S Í А× А, то, определив Р{х,у) как предложение пара (х у) принадлежит множеству S, мы получим предикат, область истинности которого совпадает с исходным бинарным отношением S. Таким образом, называя бинарное отношение предикатом, мы подразумеваем при этом двухместный предикат, областью истинности которого является данное отношение. Это соглашение относится и к произвольным п-арным отношениям.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.77 (0.089 с.) |
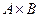 .
.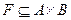 .
.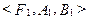 называются равными тогда и только тогда, когда
называются равными тогда и только тогда, когда 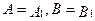 , и
, и 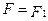 . Запись
. Запись 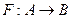 означает, что Fявляется соответствием из A в В (т.е.
означает, что Fявляется соответствием из A в В (т.е. 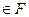 , то bназывают образом элемента aпри соответствии F. Вместо записи (а,b)
, то bназывают образом элемента aпри соответствии F. Вместо записи (а,b) 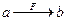 .
. А выписать множество всех его образов при данном соответствии.
А выписать множество всех его образов при данном соответствии.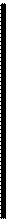

 Примеры:
Примеры: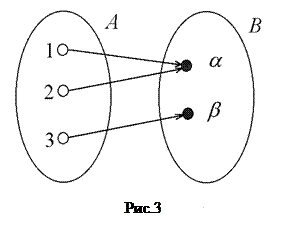
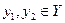 , то запись
, то запись 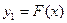 и
и 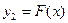 приводит к абсурду
приводит к абсурду 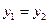 .
.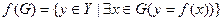
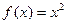 и G={ x | -1< x <2}. Тогда f(G) = { y = f(x) | 0 < y < 4}
и G={ x | -1< x <2}. Тогда f(G) = { y = f(x) | 0 < y < 4}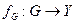 .
.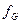 в этом случае называют сужением отображения f на множество G (рис. 4).
в этом случае называют сужением отображения f на множество G (рис. 4).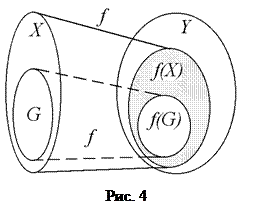
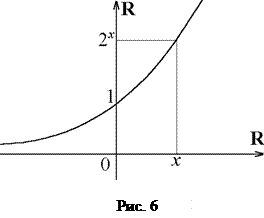
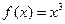 , определенное для xÎ Z, есть сужение на Z отображения
, определенное для xÎ Z, есть сужение на Z отображения 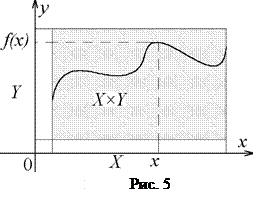
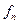 из Y.
из Y.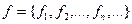 или сокращенно
или сокращенно 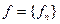 Здесь символы
Здесь символы 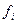 являются образами чисел из N. Например, запись
являются образами чисел из N. Например, запись 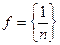 означает последовательность рациональных чисел вида
означает последовательность рациональных чисел вида 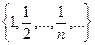 .
.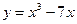 образом значений -3, 1, 2. Множество элементов х Î X, имеющих в качестве образа при отображении f один и тот же элемент у Î Y, называется множеством прообразов элемента у и обозначается
образом значений -3, 1, 2. Множество элементов х Î X, имеющих в качестве образа при отображении f один и тот же элемент у Î Y, называется множеством прообразов элемента у и обозначается  :
:
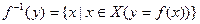
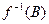 обозначается множество всех прообразов элементов, принадлежащих множеству В,
обозначается множество всех прообразов элементов, принадлежащих множеству В,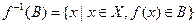
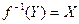 .
.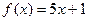 , задает сюръективное отображение множества X на множество Y.
, задает сюръективное отображение множества X на множество Y.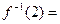 Æ.
Æ. в) Пусть снова X = У = R. Отображение f, определяемое формулой
в) Пусть снова X = У = R. Отображение f, определяемое формулой 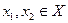 различны, т.е. из неравенства
различны, т.е. из неравенства 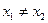 вытекает
вытекает 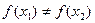 .
.
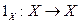 . Если X Í Y, то отображение f: X ® Y, определенное равенством f(x) = х, называют канонической инъекцией.
. Если X Í Y, то отображение f: X ® Y, определенное равенством f(x) = х, называют канонической инъекцией.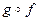 .
.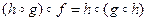 (ассоциативность композиции);
(ассоциативность композиции);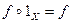 и
и 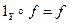 .
.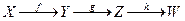 , то
, то 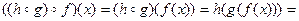
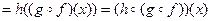 ,
,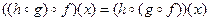 и значит
и значит 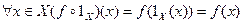 , т.е.
, т.е. 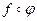 и
и 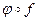 одновременно определены, но не равны между собой,
одновременно определены, но не равны между собой, 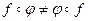 .
.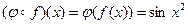 . С другой стороны,
. С другой стороны, 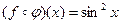 . Очевидно, что
. Очевидно, что 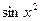 и
и  - различные функции, т.е.
- различные функции, т.е. 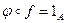 и
и 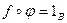 (*)
(*)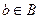 . Тогда, используя равенство
. Тогда, используя равенство 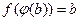 , откуда следует, что
, откуда следует, что 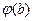 -прообраз элемента b при отображении f. Следовательно, f - сюръективно.
-прообраз элемента b при отображении f. Следовательно, f - сюръективно.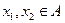 и
и 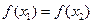 . Тогда
. Тогда 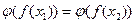 , т.е.
, т.е. 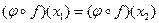 . Поскольку
. Поскольку 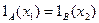 т.е.
т.е. 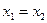 , что противоречит предположению. Поэтому
, что противоречит предположению. Поэтому 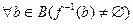 .
.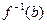 не может содержать более одного элемента и, следовательно, оно одноэлементно.
не может содержать более одного элемента и, следовательно, оно одноэлементно.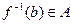 , есть отображение.
, есть отображение.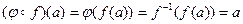
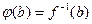 , откуда
, откуда 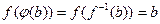 . Следовательно,
. Следовательно,  отображение, обратное к f, построенное в доказательстве теоремы 2, т.е.
отображение, обратное к f, построенное в доказательстве теоремы 2, т.е. 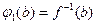
 - произвольное отображение, обратное к f. Тогда
- произвольное отображение, обратное к f. Тогда 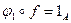 ,
, 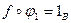 ,
, 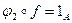 ,
, 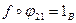 .
.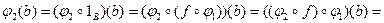
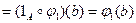
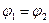 Следствие доказано. Это следствие дает основание ввести стандартное обозначение отображения, обратного к данному:
Следствие доказано. Это следствие дает основание ввести стандартное обозначение отображения, обратного к данному: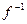 обозначается отображение, обратное к f.
обозначается отображение, обратное к f.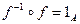 и
и 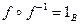

 (а) А Í В ® f(А) Í f(В) для любых подмножеств A и В множества X;
(а) А Í В ® f(А) Í f(В) для любых подмножеств A и В множества X;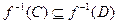 для любых подмножеств C и D множества Y.
для любых подмножеств C и D множества Y. ;
;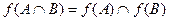 ;
;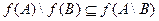 .
.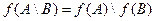 .
.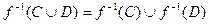 ;
; ;
;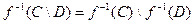 .
.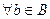 (
( Æ).
Æ).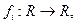
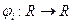 (i = 1, 2, 3) и для любого
(i = 1, 2, 3) и для любого 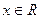
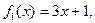
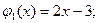
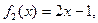
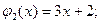
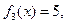
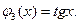
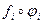 и
и 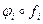 (i = 1, 2, 3).
(i = 1, 2, 3).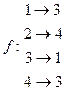
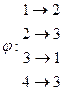
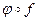 и
и  .
.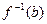 одноэлементно для любого b Î B.
одноэлементно для любого b Î B.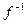 биективно и имеет место равенство
биективно и имеет место равенство 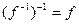 .
.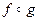 существует, то
существует, то 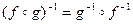 .
. §6. Бинарные и п -арные отношения
§6. Бинарные и п -арные отношения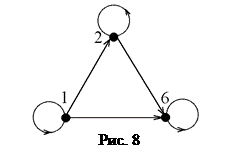
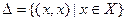 .
.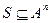 декартовой степени множества А с показателем п называется п-арным отношением на множестве А.
декартовой степени множества А с показателем п называется п-арным отношением на множестве А.


