
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разность. Универсальное множество. Дополнение.Содержание книги
Поиск на нашем сайте
ПРЕДИСЛОВИЕ В основу учебного пособия положен курс лекций, апробированный на математическом факультете Волгоградского государственного педагогического университета. "Вводный курс математики" является необходимой составной частью учебного плана подготовки будущих учителей математики. Основная задача состоит в построении общей терминологической базы, необходимой для постановки всех смежных математических дисциплин в педвузе. В этом курсе закладывается фундамент общей математической культуры: вводятся основные понятия и вырабатывается язык, который в дальнейшем используется во всех математических дисциплинах на протяжении всего периода обучения. Пособие состоит из четырех глав. В первой главе рассматриваются операции над множествами, элементы исчисления высказываний и предикатов. Глава завершается понятием об аксиоматической теории. Во второй главе изучаются соответствия, отображения, отношения, вводится понятие алгебраической системы и приводятся примеры основных классических алгебр (группоид, полугруппа, группа, кольцо и поле). В третьей главе строится эскиз аксиоматической теории натуральных чисел на базе аксиом Пеано, определяются операции сложения и умножения, вводится отношение порядка, изучаются свойства построенной системы. В ней также рассматривается связь между отрезками ряда натуральных чисел Четвертая глава естественным образом продолжает третью. Здесь строится кольцо целых чисел, вводится понятие об упорядоченном кольце и изучаются свойства упорядоченности в кольце целых чисел, обобщаются различные формы метода математической индукции для целых чисел. При написании данной книги автор хорошо осознавал, и в этом его убедила многолетняя практика, что этот курс нелегок для освоения студентами. Это объясняется в первую очередь наличием большого объема базовых понятий и, во-вторых, необходимостью его строгого изложения. Поэтому автор стремился иллюстрировать понятия примерами, с этой же целью в книге приведено около ста упражнений для самостоятельного решения.
При построении аксиоматической теории натуральных чисел все доказательства проведены подробно, что в свою очередь может вызвать обратный эффект: некое утомление читателя. В этом случае читатель может опустить излишнюю на его взгляд детализацию. Однако, по мнению автора, каждый математик и, в особенности, преподаватель математики должен хотя бы один раз в жизни детально познакомиться с доказательством основных утверждений о "первичных" объектах и отношениях, которые он постоянно использует в своей деятельности. Пособие адресовано широкому кругу читателей и, в частности, студентам-заочникам. Его программа максимально приближена к школьному курсу математики. Разделы, которые непосредственно не изучаются в школе, могут составить основу факультативных курсов. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ § 1. Понятие множества "Множество есть многое, мыслимое как единое". Г. Кантор Теория множеств как математическая дисциплина была создана немецким математиком Г. Кантором (1845-1918) во второй половине XIX в. В основе этой теории лежит одно из основных понятий математики - понятие множества. Согласно идее Г. Кантора, любое множество, являясь с одной стороны совокупностью некоторых объектов, с другой стороны рассматривается как единое целое Множество А есть любое собрание определенных и различимых между собой предметов, объектов нашей интуиции или интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества А Примеры: • множество точек плоскости; • множество корней квадратного уравнения; • множество N – натуральных чисел; • множество Z – целых чисел; • множество Q – рациональных чисел; • множество R –действительных (вещественных) чисел; • множество С – комплексных чисел; • множество книг в библиотеке; • множество городов России и т.д. К концу XIX в. теория множеств стала играть роль прочного фундамента, на который опирались другие математические дисциплины, в особенности теория функций и арифметика действительных чисел. Результаты, которые были получены с использованием понятий теории множеств, поражали своей строгостью. В адрес теории множеств было высказано много эпитетов. Крупнейший немецкий математик Д.Гильберт говорил: "Никто не может изгнать нас из рая, который создал нам Г.Кантор". Французский математик А.Пуанкаре, поразивший своих современников эрудицией и результатами исключительно во всех областях математики, выступая в 1900 году на Втором международном математическом конгрессе, сказал, что в математике "достигнута абсолютная строгость". Однако, по иронии судьбы, уже в то время было известно о наличии в теории множеств противоречий. Говорят, что теория содержит противоречие, если в ней одновременно доказуемы два утверждения, каждое из которых является отрицанием другого. В дальнейшем противоречия были названы парадоксами, В начале XX в. количество парадоксов начало расти. Это обстоятельство побудило многих крупнейших математиков заняться пересмотром основ теории множеств. Оказалось, что причины противоречия скрывались как в логике построения теории множеств, так и в несовершенстве используемого языка. Понятие множества, приведенное в начале параграфа, не может считаться определением, поскольку оно использует термины, толкование которых имеет большую свободу: "собрание определенных и различимых между собой объектов..." и т.д. Сами эти термины не имеют точного определения. Исследования вокруг проблемы построения непротиворечивой теории множеств интенсивно велись в течение всего двадцатого столетия. В результате многие парадоксы были сняты за счет "реконструкции" теории множеств. Возникли различные подходы к построению теории множеств. Обнаружились тесные связи между проблемами "оснований теории множеств", философией и математической логикой. Ревизии подверглись практически все математические дисциплины. Однако появились новые проблемы (парадоксы) другого уровня сложности. Дальнейшее освещение проблем, связанных с развитием теории множеств, выходит за рамки задач данной книги, поскольку оно требует довольно серьезных математических сведений по данному направлению. Отметим лишь, что, несмотря на "грустный" оттенок некоторых результатов, работы по пересмотру основ теории множеств привели к бурному развитию всей математики двадцатого столетия. Теория множеств является ярким примером, того, что ив математике, как и в любой другой науке, противоречия служат источником развития. Благодаря потрясениям, которые неоднократно испытывала теория множеств, она в настоящее время является фундаментом построения многих математических дисциплин. Оказалось также, что эта теория в том виде, какой она имела в конце XIX и начале XX в., после небольшой корректировки может быть использована в качестве базы построения той части математики, которая преподается в высших учебных заведениях нашей страны и за рубежом. Эту часть теории множеств называют "наивной теорией множеств". Ниже мы изложим основные понятия этой теории. Следуя Кантору, описание понятия множества будем вводить постепенно, с помощью соглашений (или требований), которым должно удовлетворять это понятие.
Говоря о множестве, мы считаем, что относительно всякого объекта верно одно и только одно из двух высказываний: либо объект входит в данное множество в качестве его элемента, либо не входит. Запись х Î А означает: х является элементом множества А, если же х не входит в А, то записывают так: х Ï А. Например, 1 Î N, –2 Ï К,
Требование Кантора, что множество определяется своими элементами, может быть сформулировано следующим образом. Интуитивный принцип объемности. Два множества равны тогда и только тогда, когда они состоят из одних и тех же элементов. Равенство двух множеств записывают в виде А = В, а неравенство множеств А и В - через А ф В. Принцип объемности означает, что для доказательства равенства множеств А и В следует выполнить два шага: 1) доказать, что если х Î А, то х Î В; 2) доказать, что если х Î В, то х Î А. Само множество по определению не является своим элементом, А Ï А. Если множество А состоит из элементов, принадлежащих некоторому другому множеству F, то оно называется подмножеством или частью этого множества. Обозначается: А Í F. Символ Í обозначает отношение включения. Например: N Í Z Í Q Í R Í C. Отношение включения множеств обладает свойствами: 1. А Í А (свойство рефлексивности), т.е. само множество является своей частью. 2. Если А Í В и В Í С, то А Í С (свойство транзитивности отношения включения). Если множество состоит только из одного элемента а, то оно называется одноэлементным и обозначается через { а }. Например, множество корней уравнения 2 х - 4 = 0 состоит из одного элемента - числа 2. § 2. Способы задания множеств 1. Множество может быть записано перечислением всех его элементов: А= { Например, В = {0,1, 2, 3,4}, ВÍ Z. 2. Обобщение первого способа состоит в том, что каждый элемент задаваемого множества определяется по некоторому элементу уже известного множества. Например, считая известным множество целых чисел Z = {..., -3,-2,-1, 0,1. 2,3,...}, определим множество степеней числа 2: D = {…, 3. Задание множества с помощью характеристического свойства Р, выделяющего элементы множества Е, среди элементов более широкого, или основного множества А. Этот способ исходит от Кантора в следующем виде: "Каждое свойство определяет некоторое множество". Четкая формулировка его использует понятие "формы от x " или "формулы от x ". Для первоначального ознакомления под формой от x будем понимать некоторое повествовательное предложение Р(х), содержащее переменное x, которое становится истинным или ложным высказыванием при подстановке вместо x конкретного значения а. Таким образом, форма от x - это некоторое утверждение об x. Интуитивный принцип абстракции. Любая форма Р(х) определяет некоторое множество А, элементами которого являются в точности такие предметы а, для которых Р(а) - истинное высказывание.
Это множество обозначается через { x | Р(х) }и читается: множество всех х, которые обладают свойством Р. Примеры:
4. В дальнейшем мы увидим, что новые множества могут быть заданы при помощи некоторых операций над исходными множествами. Из принципа абстракции следует существование множества { x | х ¹ х }. Это множество, очевидно, не имеет элементов. Из принципа объемности вытекает, что такое множество одно. Оно называется пустым и обозначается символом Æ. Пустое множество Æ является подмножеством любого множества. Действительно, если предположить, что включение Æ Í А ложно, то тогда найдется элемент, принадлежащий множеству Æ и не принадлежащий множеству А. Но это невозможно, поскольку Æ не имеет элементов. Множеством подмножеств некоторого фиксированного множества А называется множество, элементами которого являются подмножества множества А. Это множество Р(А) содержит в качестве элементов пустое множество Æ и само множество А. Например, если А = { а, b, с }, то Р(А) = {Æ, { а }, { b }, { c },{ a, b },{ а, с }, { b, c }, { а, b, с }}. § 3. Операции над множествами Объединение. Пересечение. Объединением множеств А и В называется множество А и В, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств, т.е. А
Объединение семейства {
Пересечением множеств А и В называется множество А∩В, состоящее из всех общих элементов данных множеств, т.е. А
Если таких элементов не существует, то А Пересечение семейства множеств {
Заметим, что рисунки, приведенные выше для иллюстрации операций над множествами, принято называть диаграммами Эйлера - Венна. Примеры: 1. Пусть А = {2,5,7}, В = {1,5,8}. Тогда А 2. Если А = { х | х Î R, x ³ 0 }, В = { х | х Î R, –2 £ х £ 2}, то А 3. Пусть А–множество всех целых, делящихся на 3, а В – множество всех четных целых чисел. Тогда А Формулы логики высказываний Аналогично тому, как в алгебре с помощью арифметических операций строят сколь угодно сложные выражения из символов, обозначающих переменные величины, так и в логике определенные выше логические операции применяются для построения из данных высказываний новых, более сложных. Ниже мы дадим определение формулы логики высказываний. Буквы А, В, С… либо
1. Всякая высказывательная переменная есть формула. 2. Символы И и Л – формулы. 3. Если 4. Если 5. Никаких других формул, кроме полученных в соответствии с правилами 1 – 4, не существует. Замечание. Это определение перечисляет правила построения новых формул из любого множества исходных формул. Определения такого типа называются индуктивными. Также, как в арифметике, скобки (,) служат для указания последовательности действий при построении формулы. Для упрощения записи формул примем следующие соглашения об опускании скобок: 1) Будем говорить, что каждый из знаков в ряду Ø, Ù, Ú, ®, «"сильнее" любого из знаков, следующих за ним в указанном порядке, т.е. отрицание Ø "сильнее" конъюнкции Ù, которая, в свою очередь, "сильнее" дизъюнкции Ú и т.д. 2) Будем считать возможным опускать внешние скобки, например, вместо записи ( 3) Остальные скобки опускаются таким образом, чтобы при их восстановлении из двух операций более "сильная" выполнялась раньше. В этом случае формула может быть названа § 6. Булевы функции Как уже отмечалось, строение формулы позволяет определить ее значение истинности в зависимости от набора значений истинности элементарных формул, из которых они построены (образованы). Это означает, что каждая формула определяет некоторую функцию, которая сама и ее аргументы принимают одно из значений И или Л. Такие функции называются булевыми или функциями алгебры логики. Например, формулу Формула Например, тавтологиями являются следующие формулы Формула Например, формула Равносильные формулы. Две формулы Таким образом, две формулы равносильны в том и только в том случае, если они принимают одинаковые значения истинности при любом наборе значений истинности составляющих их элементарных формул. Поэтому в равносильности двух формул можно убедиться сопоставлением их таблиц истинности. Например, из таблицы истинности очевидным образом усматривается равносильность формул
Из определения непосредственно вытекает утверждение: "Две формулы Равносильности формул играют важную роль в логических рассуждениях. Поэтому их часто называют законами логики. Приведем основные из них: I. А ÚØА≡ И (закон исключенного третьего). II. А ÙØA≡ Л (закон противоречия). III. ØØAºA(закон двойного отрицания). IV. А º А(закон тождества). V. А ÚВ = В Ú А, А Ù В = В Ù А (законы коммутативности). VI. А Ú А = А, А Ù А = А(законы идемпотентности). VII. А Ú(В ÚС) º (А Ú В) ÚС, А Ù (В Ù С) º (А Ù В) Ù С VIII. А Ù (В Ú С) º (А Ù В) Ú (А Ù С)(закон дистрибутивности IX. АÚ(ВÙС) º (АÚВ)Ù(АÚС)(закон дистрибутивности дизъюнкции относительно конъюнкции). X. А Ù (А ® В) ® В º И (закон отделения). XI. (А ® В) Ù (В ® С) ® (А ® С) ≡ И (закон силлогизма). XII. А ® В ≡ ØА Ú В (закон исключения импликации). XIII. А Ú В ≡ ØА ®В(закон исключения дизъюнкции). XIV. Ø(АÚВ) ≡ ØАÙØВ, Ø(АÙВ) ≡ ØАÚØВ(законы де Моргана). XV. А ® В ≡ ØВ ®ØА(закон контрапозиции). Убедиться в справедливости каждой из перечисленных выше равносильностей можно, например, с помощью сопоставления таблиц истинности для формул, стоящих в левой и правой частях каждой из них. Этого можно добиться, не прибегая к таблицам истинности. В качестве примера докажем равносильность формул Ø(A Ú В) и ØАÙØВ. Допустим, что формула Ø(A Ú В) принимает значение И, тогда формула А Ú В принимает значение Л. Это означает, что каждая из формул А и В принимает значение Л, откуда следует, что формулы ØА и ØВ одновременно принимают значение И, т.е. ØА Ù ØВпринимает значение И. Пусть Ø(АÚВ)принимает значение Л. Тогда АÚВимеет значение И. Это означает, что хотя бы одна из формул А или В принимает значение И, откуда в свою очередь следует, что хотя бы одна из формул ØА, ØВимеет значение Л и, следовательно, ØА Ù ØВпринимает значение Л. Таким образом, Ø(A Ú В) ≡ ØАÙØВ. Логическое следствие. Пусть Будем говорить, что формула
если формула Ψ принимает значение И при всех наборах значений истинности элементарных формул Из определения непосредственно вытекает:
Например,A├ A Ú В, А Ù В├A для любых формул А и В. Определение логического следствия можно распространить на любое количество посылок следующим образом: “Формула Непосредственным образом проверяется справедливость следующего утверждения
ГЛАВА II Соответствие Пусть A, В-множества. Соответствием из A в В называется произвольное подмножество Fдекартова произведения При этом множество Aназывается областью отправления соответствия F, а B-его областью прибытия. Таким образом, всякое соответствие определяется тройкой множеств < F, A, B>, где Два соответствия < F, A, B> и Если (а, b) Таким образом, множество F можно рассматривать как некоторое множество стрелок, начало которых принадлежит области отправления соответствия, а конец - области прибытия. Если множества А и В зафиксированы, то для задания соответствия из A в В достаточно определить множество F. Для этого следует указать правило, позволяющее для каждого элемента а
1. Пусть А = {1,2,3},В = {a, b}, F ={(1,a),(2,a),(2,b)} 2. Пусть А, Втакие же, как и в предыдущем пункте. Тогда то же множество F может быть указано как множество стрелок (рис. 3). 3. Пусть А = В = N - множество положительных целых чисел. Множество Fесть область истинности предиката " х - делитель у ", т.е. F= {(x, у) \ x - делитель у}.
 §2. Отображение (функция) §2. Отображение (функция)
В общей ситуации не каждый элемент из области отправления соответствия обязан иметь образ или, напротив, он может иметь более одного образа. Если каждый элемент области отправления соответствия имеет единственный образ, то такое соответствие называется отображением, или функцией. Для отображений принята специальная терминология: область отправления именуется областью определения; а область прибытия - областью значений. Подчеркнем, что отображение f: X ® Y определено лишь в том случае, когда каждый элемент х Î X имеет во множестве Y единственный образ у ÎY. Это обстоятельство записывается в виде равенства y = f(x), которое обозначает, что "элемент у есть образ элемента х при отображении f " или "элемент х есть прообраз элемента у при отображении f ". Отметим, что в общем случае для соответствия F использование равенства у = F (х) может привести к противоречию. Например, если при соответствии F: X ® Y элемент x Î X имеет два различных образа Если множество G Í X, то через f(G) обозначается множество образов всех элементов множества G:
Множество f(G)называется образом множества G при отображении f. Пример. Пусть отображение f:R®R определяется как § 3. Сужение отображения. График. Последовательность Пусть имеем отображение f: X ® Y, и пусть G Í X. Тогда отображение f всякому элементу из G ставит в соответствие некоторый элемент из Y, стало быть, оно определяет отображение Отображение
П р и м е р 1. Отображение Множество пар { x, f(x) }, являющееся подмножеством произведения Х ´ Y, называется графиком функции f(x) (рис. 5).
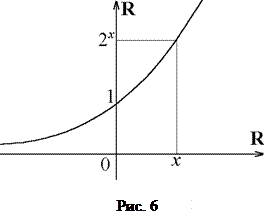
П р и м е р 2. Множество пар 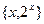 являющееся подмножеством произведения являющееся подмножеством произведения 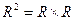 , составляет график; показательной функции , составляет график; показательной функции 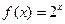 (рис. 6). (рис. 6).
Возьмем N - множество натуральных чисел, в качестве Y -произвольное множество. Отображение f: N ®Y называется последовательностью элементов из Y. Таким образом, последовательность f связывает каждое натуральное число п с некоторым элементом Последовательность f будем обозначать § 4. Типы отображений Пусть f: X ® Y - отображение. Тогда каждому элементу х Î X соответствует единственный элемент у Î Y, с другой стороны, элемент у Î Y может быть образом нескольких элементов из X. Например, значение -6 служит для функции
Пусть В Í Y, Тогда через
1. Отображение f: X ® Y называется сюръективным, или сюръекцией, или отображением, на множество Y, если каждый элемент у Î Y из области его значений имеет хотя бы один прообраз, т.е. множество Очевидно, что отображение f: X ® Y является сюръекцией тогда и только тогда, когда f(X) = Y. Заметим, что в этом утверждении равенство f(X) = Y можно заменить равносильным ему равенством: Примеры: а) Пусть X = У = R. Отображение f, определяемое формулой б) Пусть X = У = R. Отображение f, определяемое формулой
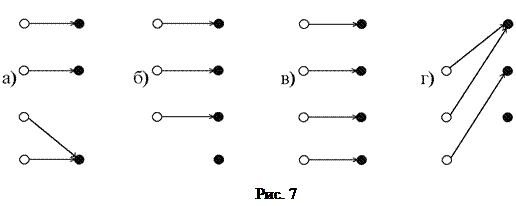
2. Говорят, что отображение f: X ® Y является взаимнооднозначным или инъективным, если образы любых двух различных элементов 3. Отображение f: X ® Y называют биективным или биекцией, если оно одновременно инъективно и сюръективно, т.е. если каждый элемент Y является образом некоторого единственного элемента из X. Примеры: Отображение, заданное на рисунках: 7 а) - сюръективно, но не инъективно; 7 б) - инъективно, но не является сюръекцией; 7 в) - биекция;
7 г) - не обладает ни одним из указанных свойств. Отображение f: X ® Y, определенное равенством f(x) = х, называется тождественным, и обозначается: § 5. Композиция отображений, обратимые отображения Пусть X, Y, Z - множества f: X ® Y и g: Y ® Z - отображения. Отображение h: X ® Z, определяемое формулой h(x) = g(f(x)) называется композицией, или суперпозицией, или произведением отображений f и g и обозначается через В том случае, когда f и g именуются функциями, Теорема 1. Композиция отображений обладает следующими свойствами: 1) если f: X ® Y, g: Y ® Z и h: Z ® W - отображения, то
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.37 (0.012 с.) |

 и конечными множествами. Глава завершается обоснованием различных форм метода математической индукции (для натуральных чисел).
и конечными множествами. Глава завершается обоснованием различных форм метода математической индукции (для натуральных чисел).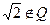 .
.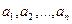 }.
}.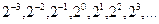 }.
}. означает множество положительных действительных чисел;
означает множество положительных действительных чисел; - множество всех корней уравнения
- множество всех корней уравнения  .
.  В = { а| а Î А или а ÎВ }.
В = { а| а Î А или а ÎВ }.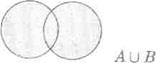 В частности, если множества А и В заданы с помощью характеристических свойств, например, А = { а| Р(а) }, В = { b| Q(b) }, то объединение состоит из всех тех элементов, которые обладают хотя бы одним из свойств Р или Q.
В частности, если множества А и В заданы с помощью характеристических свойств, например, А = { а| Р(а) }, В = { b| Q(b) }, то объединение состоит из всех тех элементов, которые обладают хотя бы одним из свойств Р или Q. } множеств
} множеств  , занумерованных некоторым множеством I индексов, обозначается через
, занумерованных некоторым множеством I индексов, обозначается через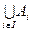
 В= { а|а Î А и а Î В }.
В= { а|а Î А и а Î В }.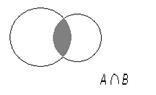
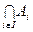 .
.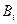 ,
, 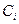 (I Î N) будут использованы для обозначения исходных или элементарных высказываний. Эти символы называются высказывательными переменными. Понятие формулы логики высказываний определяется следующими соглашениями:
(I Î N) будут использованы для обозначения исходных или элементарных высказываний. Эти символы называются высказывательными переменными. Понятие формулы логики высказываний определяется следующими соглашениями: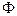 – формула, то (
– формула, то (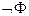 ) – формула.
) – формула.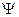 – формулы, то (
– формулы, то (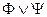 ), (
), (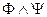 ), (
), (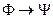 ), (
), ( ) – формулы.
) – формулы. по "последней" операции. Например, вместо записи
по "последней" операции. Например, вместо записи  получим импликацию
получим импликацию 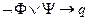 .
. можно рассматривать как выражение для функции
можно рассматривать как выражение для функции  ,
, 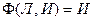 ,
, 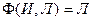 и
и 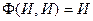 .
. логики высказываний называется тождественно истинной или тавтологией, если она принимает значение И при любом наборе значений истинности элементарных формул
логики высказываний называется тождественно истинной или тавтологией, если она принимает значение И при любом наборе значений истинности элементарных формул 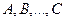 , из которых она построена.
, из которых она построена.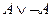 ,
, 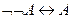 ,
, 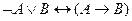 .
. тождественно ложна.
тождественно ложна. называются равносильными, если они определяют одну и ту же булеву функцию. Запись
называются равносильными, если они определяют одну и ту же булеву функцию. Запись 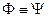 означает равносильность формул.
означает равносильность формул. и
и 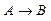
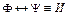 ".
".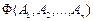 и
и 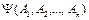 - две формулы логики высказываний, построенные из элементарных формул
- две формулы логики высказываний, построенные из элементарных формул 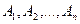 .
. является логическим следствием формулы
является логическим следствием формулы  , что записывается так:
, что записывается так: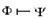 тогда и только тогда, когда
тогда и только тогда, когда , если
, если 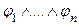 ├
├ 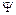 . (2)
. (2)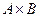 .
.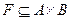 .
.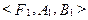 называются равными тогда и только тогда, когда
называются равными тогда и только тогда, когда 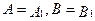 , и
, и 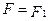 . Запись
. Запись 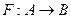 означает, что Fявляется соответствием из A в В (т.е.
означает, что Fявляется соответствием из A в В (т.е. 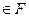 , то bназывают образом элемента aпри соответствии F. Вместо записи (а,b)
, то bназывают образом элемента aпри соответствии F. Вместо записи (а,b) 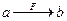 .
. А выписать множество всех его образов при данном соответствии.
А выписать множество всех его образов при данном соответствии.

 Примеры:
Примеры: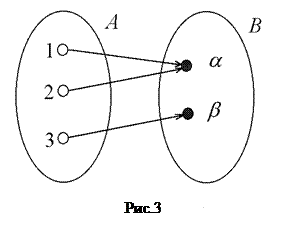
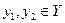 , то запись
, то запись 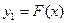 и
и 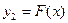 приводит к абсурду
приводит к абсурду 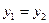 .
.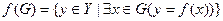
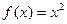 и G={ x | -1< x <2}. Тогда f(G) = { y = f(x) | 0 < y < 4}
и G={ x | -1< x <2}. Тогда f(G) = { y = f(x) | 0 < y < 4} .
. в этом случае называют сужением отображения f на множество G (рис. 4).
в этом случае называют сужением отображения f на множество G (рис. 4).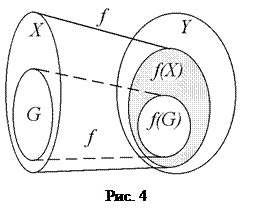
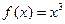 , определенное для xÎ Z, есть сужение на Z отображения
, определенное для xÎ Z, есть сужение на Z отображения 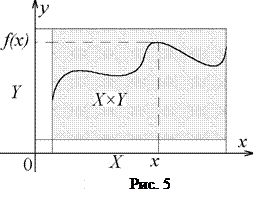
 из Y.
из Y.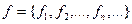 или сокращенно
или сокращенно 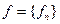 Здесь символы
Здесь символы 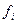 являются образами чисел из N. Например, запись
являются образами чисел из N. Например, запись 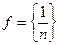 означает последовательность рациональных чисел вида
означает последовательность рациональных чисел вида 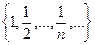 .
.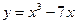 образом значений -3, 1, 2. Множество элементов х Î X, имеющих в качестве образа при отображении f один и тот же элемент у Î Y, называется множеством прообразов элемента у и обозначается
образом значений -3, 1, 2. Множество элементов х Î X, имеющих в качестве образа при отображении f один и тот же элемент у Î Y, называется множеством прообразов элемента у и обозначается  :
:
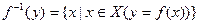
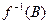 обозначается множество всех прообразов элементов, принадлежащих множеству В,
обозначается множество всех прообразов элементов, принадлежащих множеству В,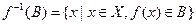
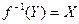 .
.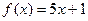 , задает сюръективное отображение множества X на множество Y.
, задает сюръективное отображение множества X на множество Y.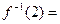 Æ.
Æ. в) Пусть снова X = У = R. Отображение f, определяемое формулой
в) Пусть снова X = У = R. Отображение f, определяемое формулой 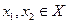 различны, т.е. из неравенства
различны, т.е. из неравенства 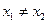 вытекает
вытекает 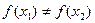 .
.
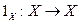 . Если X Í Y, то отображение f: X ® Y, определенное равенством f(x) = х, называют канонической инъекцией.
. Если X Í Y, то отображение f: X ® Y, определенное равенством f(x) = х, называют канонической инъекцией.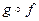 .
.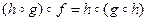 (ассоциатив
(ассоциатив


