Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие об аксиоматической теорииСодержание книги Поиск на нашем сайте
Одной из особенностей математики двадцатого столетия является построение аксиоматических теорий во многих ее областях. Аксиоматический подход использовался еще Евклидом в его "Началах" при изложении основ классической геометрии, но лишь в двадцатом столетии он получил широкое распространение. "Начала" Евклида построены следующим образом. Сначала были выделены так называемые первичные объекты, точка, прямая и плоскость. Затем сформировались предложения, описывающие отношения между первичными объектами. Некоторые из них он назвал аксиомами, другие - постулатами. Далее с помощью первичных объектов определялись некоторые другие вспомогательные понятия, затем из аксиом и постулатов выводились новые свойства первичных и определенных с их помощью объектов. Эти свойства назывались теоремами. Евклид считал, что значения таких терминов, как “точка”, "прямая" и "плоскость" достаточно ясны, и относящиеся к ним аксиомы - "самоочевидные истины". Такое толкование термина "аксиома" широко распространено и в наше время в нематематических текстах. Внутри самой математики это понятие претерпело значительную эволюцию. Первым шагом в этом направлении было открытие Н.И.Лобачевским и (независимо от него) венгерским математиком Я.Бойаи неевклидовой геометрии. Список аксиом этой геометрии получается из списка аксиом евклидовой геометрии заменой аксиомы параллельности (пятого постулата) ее отрицанием. А именно, этот постулат в геометрии Лобачевского формули Аксиоматическая теория строится следующим образом. Фиксируется некоторое множество S логических формул, например, формул исчисления высказываний. Никакого значения истинности заранее этим формулам не приписывается. Без ущерба для общности в дальнейшем вместо слов "логическая формула" будем употреблять термин "высказывание". Формулы, входящие в S, называются аксиомами (первичные предложения). Далее рассматриваются всевозможные конечные последовательности высказываний
удовлетворяющие специальным требованиям: каждое высказывание, входящее в последовательность (*), является либо аксиомой, то есть принадлежит исходному множеству S, либо тавтологией, либо получается из предыдущих высказываний последовательности (*) по некоторым правилам (схемам) вывода. Правила вывода фиксируются заранее. Они устроены таким образом, что в процессе их применения из предложений, к которым они применяются, получается их логическое следствие. Любая последовательность высказываний Любое высказывание А, которое входит в некоторое доказательство (то есть совпадает с одним из высказываний Таким образом, под теорией подразумевается множество всех предложений, выводимых из данного множества Sаксиом Сделаем несколько очевидных следствий из определения логического вывода. 1. Любая аксиома данной теории является теоремой. Это утверждение справедливо и для любой тавтологии. 2. Очевидно, если в логическом выводе, начиная с некоторого номера i, отбросить все высказывания, то снова получится вывод из S, то есть, если 3. Если 4. Чрезвычайно важным обстоятельством является следующий факт, который легко усматривается из определения логического вывода: каждое высказывание, входящее в любой вывод из данной системы S аксиом, является логическим следствием из данной системы аксиом. Отсюда вытекает: если каждая аксиома из 3 истолкована каким-либо способом как истинное предложение о некоторой совокупности объектов, то каждая теорема в теории (для которой S служит системой аксиом) также будет истинным утверждением о тех же объектах. Данное описание принципов построения аксиоматической теории не претендует на полноту изложения. Глубокое понимание этих принципов может прийти к читателю лишь после знакомства с конкретными аксиоматическими теориями. Заметим, что каждая тавтология является логическим следствием любых посылок. Поэтому любая тавтология может быть принята за основу некоторого правила вывода. Приведем наиболее употребительные правила вывода. 1. Правило отделения (modus ponens) Выглядит оно следующим образом: A, A®B├B В словесной формулировке оно звучит так: "Если оба высказывания А и А ® В- истинны, то и В истинно". Это правило основано на тавтологии (X): А Ù (А ® В) ® В. Из нее согласно (1) имеем А Ù(А ®В)├ B, откуда, ввиду (2), получим A, (A®B)├B 2. Правило контрапозиции А ® B├ Ø В ® Ø А. В основе его лежит закон контрапозиции (XV): А ® В ≡ ØВ ®Ø A. Действительно, согласно (XV) формула А ® В ® ØВ ®Ø A является тавтологией, откуда, в силу (2), А ® B├ Ø В ® Ø А. Например, правильность рассуждения: "В параллелограмме диагонали точкой пересечения делятся пополам. Следовательно, если в четырехугольнике диагонали точкой пересечения не делятся пополам, то четырехугольник не является параллелограммом" - гарантируется законом контрапозиции. 3. Правило силлогизма Позволяет в любом логическом выводе при наличии в нем высказываний А ® В и В ® С поставить высказывание А ® С. Это правило основано на законе силлогизма (XI). Оно может быть записано в следующем виде: А ® В, В ® С├ А ® С
Другие правила будут приведены в упражнениях (см. с. 34). О методах доказательств. При проведении математических рассуждений часто применяются различные "процедуры" позволяющие избегать "излишних" построений при решении вопроса, является ли данное высказывание логическим следствием конкретной системы посылок. Некоторые из таких наиболее часто применяемых процедур получили название метода доказательств. 1. Одним из таких методов является метод вспомогательной гипотезы. Он основан на следующем свойстве логического следствия:
Это свойство обычно называют "теоремой дедукции". Справедливость легко устанавливается с помощью определений логического следствия и операции импликации. В практике чаще всего "теорема дедукции" используется следующим образом: для построения вывода из посылок Тогда в силу "теоремы дедукции" высказывание А ® В является логическим следствием посылок 2. Метод " от противного". По установившейся традиции тождественно-ложное высказывание вида СÙØСбудем называть "противоречием". Основанием метода "от противного" служит следующее предложение: Для вывода высказывания В из посылок Действительно, пусть Тогда по "теореме дедукции" Допустим теперь, что каждая из посылок Метод "от противного" чаще всего применяется в сочетании с методом введения вспомогательной гипотезы по следующей схеме. Допустим, что надо установить
По "теореме дедукции" достаточно показать, что Для этой цели в соответствии с методом "от противного" достаточно проверить, что для некоторого высказывания С выполняется
Таким образом, для установления логического следствия (3) достаточно к системе посылок добавить посылки А ® В и из новой системы посылок вывести "противоречие". На практике это введение новых посылок осуществляю словами: "Пусть А истинно, но В ложно", и далее идет поиск противоречия. 3. Метод разделения случаев опирается на следующее легко проверяемое свойство: если Доказательство теоремы 1. Рассматривается случай, когда А истинно, и доказывается, что тогда и С истинно. Этим самым устанавливается, что
2. Затем показывают, что в случае, если В истинно, то
3. После этого делается заключение, что
Как уже отмечалось, утверждения, рассматриваемые в математике, имеют, как правило, форму импликации: "Если А, то В". Например, в утверждении: "Если дискриминант Доказательство любого утверждения, имеющего форму импликации А ® В, состоит в построении вывода утверждения В из аксиом и утверждения А (см. метод вспомогательной гипотезы). Если такое доказательство осуществимо, то говорят, что А является достаточным условием для В, а В - необходимым условием для А. Например, в утверждении: "Если произведение двух натуральных чисел делится на простое число, то на него делится один из сомножителей", высказывание "произведение двух натуральных чисел делится на простое число" является достаточным условием для высказывания "на простое число делится один из сомножителей", а второе высказывание - необходимым условием для первого. Допустим теперь, что справедливы оба утверждения А ® В и В ® А. Тогда каждое из двух высказываний А и В является одновременно и необходимым и достаточным условием для другого, и эти высказывания равносильны. Поэтому утверждение (высказывание), что А является необходимым и достаточным условием для В, записывают в виде Построим из высказываний А и В с помощью отрицания и импликации следующие утверждения: 1. 2. 3. 4. Утверждения 1, 2, так же, как и утверждения 3 и 4, называются взаимно обратными. Утверждения 1 и 3 (значит, и утверждения 2 и 4) называются взаимно противоположными. Простые примеры показывают, что истинность или ложность одного из двух взаимно обратных (или противоположных) утверждений не влечет за собой, вообще говоря, ни истинности, ни ложности другого высказывания. Например, если А- утверждение "четырехугольник является ромбом", В- утверждение "диагонали четырехугольника взаимно перпендикулярны", то утверждение Заметим, что по закону " контрапозиции" высказывания 1 и 4, а также 2 и 3 равносильны между собой. Ясно, что если утверждение А ® В есть теорема, то обратное утверждение В ® Аравносильно первому тогда и только тогда, когда В есть необходимое и достаточное условие для А. В этом случае все четыре утверждения равносильны, т.е. являются теоремами и носят следующие названия:
§ 8. Предикаты Рассмотрим предложение "х есть четное число". Его нельзя назвать высказыванием, поскольку невозможно решить вопрос, является ли это предложение истинным или ложным. Но оно становится высказыванием, как только переменная x принимает какое-нибудь конкретное значение. Таким образом, данное предложение определяет некоторую функцию, заданную на множестве Z целых чисел со значениями во множестве {И, Л}. В более общей ситуации будем говорить, что на множестве X задан предикат, от переменных Примеры: 1. На множестве N натуральных чисел задан предикат Р(х): "х есть простое число". Тогда, например, запись P(3) -И будет означать, что предикат при х = 3 превращается в истинное высказывание, т.е. "3 - простое число", а Р(6)-Л означает, что число 6 не является простым. 2. На множестве рассмотрим предикат Q (х,у): "х является делителем у ". Очевидно, что Q (2, 6) - И, а Q (3,10) - Л. Если на множестве X задан п- местный предикат
всех наборов Очевидно, что для задания предиката на множестве X достаточно указать его область истинности. Логические операции над предикатами. К предикатам применимы все операции логики высказываний. Это обстоятельство дает возможность образовывать из некоторых фиксированных предикатов новые, более сложные. Например, пусть на множестве X заданы два предиката P(x) и Q(х). Тогда дизъюнкцией их называется предикат P(x) Ú Q(х), который превращается в ложное высказывание при тех и только тех значениях переменного х Î X, при которых каждый из предикатов P(x), Q(х) превращается в ложное высказывание. Аналогично определяются операции: отрицание, конъюнкция, импликация и эквиваленция. Эти определения естественным образом распространяются на случай многоместных предикатов.
Предикат называется тождественно ложным, если его область истинности пуста, т.е. Р(а) - Л для любого элемента а Î А. Кванторы. Всякому одноместному предикату Р(х) на множестве А поставим в соответствие высказывание Из предиката Р(x) можно построить другое высказывание Высказывание Знак Применение этой операции к одноместному предикату по определению превращает этот предикат в высказывание. Навешивание квантора на многоместный предикат понижает местность этого предиката на единицу. Например, если на множестве А задан двухместный предикат Р(х, у), то предложение По этой причине переменную, которая связывается квантором, называют связанной, а переменную, не связанную квантором,- свободной. Кванторы Например, пусть f(x) - функция действительного переменного. Тогда истинность высказывания
означает, что Т - период функции f(x). Если высказывание
истинно, то b является пределом функции f(x) в точке x. Законы логики предикатов. Пусть Р(х) и Q(x) - предикаты, определенные на множестве A. Будем говорить, что предикат Р(х) равносилен предикату Q(x), и записывать Р(х) = Q(x), если они принимают одинаковые значения истинности при любом значении переменного х Î А. Аналогично определяется отношение равносильности для многоместных предикатов. Очевидно, что предикаты Р(х) и Q(х) равносильны тогда и только тогда, когда их эквиваленция Р(х) «Q(x) является тождественно истинным предикатом. Равносильности предикатов играют такую же роль в логических рассуждениях, как и равносильности формул логики высказываний. Поэтому их также называют законами логики. Приведем наиболее употребительные из них. 1. " х " уР(x,у) ≡ " у " хР(х,у), $ х $ уР(х,у) ≡ $ у $ хР{х,у) (перестановочность одноименных кванторов). 2. " х (Р(x) Ù Q (x)) ≡" x Р(х) Ù" xQ(x) (дистрибутивность квантора общности относительно конъюнкции). 3. $ х (Р(x) Ú Q (x)) ≡$ x Р(х) Ú$ xQ(x) (дистрибутивность квантора относительно конъюнкции). 4. Ø" xP(x) º$ x Ø P(x) (закон отрицания квантора общности). 5. Ø$ х Р(х) º" x Ø P(x) (закон отрицания квантора существования). Равносильности 4 и 5 по традиции называются законам де Моргана логики предикатов. Доказательство каждой из вышеприведенных равносильностей легко следует из определений. В качестве примера убедимся в справедливости закона отрицания квантора существования 5. Пусть, например, высказывание Ø$ х Р(х) истинно. Том да высказывание $х Р(х) ложно. Это означает, что Р(х) - тождественно ложный предикат, а значит, Ø Р(х)- тождественно истинный предикат. Следовательно, высказывание " x Ø Р(x) истинно. Обратно, пусть " x Ø Р(x) - истинное высказывание. Проделав предыдущие рассуждения в обратном порядке, получим что высказывание Ø$ х Р(х) также истинно. Таким образом, Ø$ х Р(х) º " x Ø Р(x). Упражнения: 1. Докажите справедливость утверждения: формулы F и Y логики высказываний равносильны тогда и только тогда, когда их конъюнкция Ф «Y является тавтологией. 2. Докажите равносильности I-ХV, указанные на с. 21. 3. Докажите справедливость утверждений для любых формул логики высказываний: (а) если (б) если Ф├ 4. F º Y тогда и только тогда, когда Ф ├ Y и Y├Ф. 5. Если Ф ├ Y и Y ├ Q, то Ф ├ Q. 6. Обосновать следующие правила вывода для любых формул А, В логики высказываний: a) A ├ A Ú B; b) А,В├ АÙ В; c) ØА ├ А ® В; d) А Ú В, Ø А ├ В; e) AÙB├A; f) А ® В, ØВ ├ А. 7. Найти области истинности предикатов, заданных на множестве А = {1,3,4,6,7,9,12}: a) Р(х): " х - нечетное число"; b) Q(х,у):"х -делитель у"; c) S (х, у, z): "разность (x - у) делится на z ". 8. На множестве X заданы предикаты Р(x) и Q(x). a) Сформулировать определение каждой из операций Ø, Ù, Ú, ®, «над предикатами Р(x) и Q(х). b) Пусть 9. Пусть a) b) 10. Докажите основные равносильности 1-4, приведенные на с. 33. 11. Пусть Р(x, у, z) - предикат, определенный на множестве A. a) Какие из следующих предикатов являются одноместными предикатами и от какой переменной:
b) 12. Докажите, что следующие высказывания являются истинными: a) b) c) 13. Привести пример предиката 14. Построить отрицания к следующим предложениям:
b. c. d. ГЛАВА II
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.149.55 (0.01 с.) |

 руется следующим образом: Если на плоскости точка А не лежит на прямой l, то существует более чем одна прямая, проходящая через А и параллельная l. Мы хорошо знаем, сколь велико было сомнение современников Н.И.Лобачевского в "истинности" новой геометрии. Подробное освещение исторических фактов, связанных с развитием и становлением геометрии Лобачевского, выходит за рамки этой книги. Скажем лишь, что впоследствии, в связи с построением различных интерпретаций неевклидовой геометрии, изменилось отношение к аксиоматической теории и ее роли в математике.
руется следующим образом: Если на плоскости точка А не лежит на прямой l, то существует более чем одна прямая, проходящая через А и параллельная l. Мы хорошо знаем, сколь велико было сомнение современников Н.И.Лобачевского в "истинности" новой геометрии. Подробное освещение исторических фактов, связанных с развитием и становлением геометрии Лобачевского, выходит за рамки этой книги. Скажем лишь, что впоследствии, в связи с построением различных интерпретаций неевклидовой геометрии, изменилось отношение к аксиоматической теории и ее роли в математике.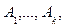 (*)
(*)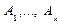 , построенная описанным выше способом, называется доказательством или логическим выводом из S. В некоторых случаях аксиомы, входящие в логический вывод, называются посылками (этого вывода).
, построенная описанным выше способом, называется доказательством или логическим выводом из S. В некоторых случаях аксиомы, входящие в логический вывод, называются посылками (этого вывода).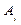 последовательности (*)), называется выводимым из S или теоремой теории, аксиомами которой служат высказывания, входящие в исходное множество S.
последовательности (*)), называется выводимым из S или теоремой теории, аксиомами которой служат высказывания, входящие в исходное множество S.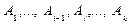 - логический вывод из S, то
- логический вывод из S, то 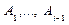 также является логическим выводом из S. Поэтому наряду с приведенными определениями можно встретить следующее: "Высказывание В называется выводимым из множества высказываний S, если существует логический вывод
также является логическим выводом из S. Поэтому наряду с приведенными определениями можно встретить следующее: "Высказывание В называется выводимым из множества высказываний S, если существует логический вывод 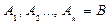 , последним звеном которого служит это высказывание".
, последним звеном которого служит это высказывание".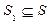 , где
, где 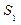 есть множество всех аксиом, входящих в данный логический вывод.
есть множество всех аксиом, входящих в данный логический вывод.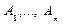 ├ A® В тогда и только тогда, когда
├ A® В тогда и только тогда, когда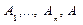 ├ В
├ В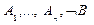 логически следует некоторое "противоречие"'.
логически следует некоторое "противоречие"'. (3)
(3)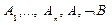 ├
├ 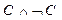
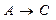 и
и 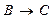 , то
, то 
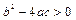 , то квадратное уравнение
, то квадратное уравнение 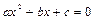 имеет два различных действительных корня" высказывание "дискриминант
имеет два различных действительных корня" высказывание "дискриминант 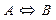 . Читается: " А необходимо и достаточно для В ", "А имеет место тогда и только тогда, когда справедливо В ". Например, высказывание "Диагонали четырехугольника точкой их пересечения делятся пополам" необходимо и достаточно для высказывания "Четырехугольник является параллелограммом".
. Читается: " А необходимо и достаточно для В ", "А имеет место тогда и только тогда, когда справедливо В ". Например, высказывание "Диагонали четырехугольника точкой их пересечения делятся пополам" необходимо и достаточно для высказывания "Четырехугольник является параллелограммом".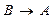 (“если B, то A”).
(“если B, то A”).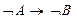 (“если не A, то не B”).
(“если не A, то не B”).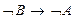 (“если не B, то не A”).
(“если не B, то не A”).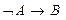 - ложно.
- ложно.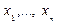 или n-местный предикат
или n-местный предикат 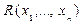 , если каждому набору значений этих переменных поставлено в соответствие вполне определенное значение истинности: И или Л.
, если каждому набору значений этих переменных поставлено в соответствие вполне определенное значение истинности: И или Л.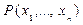 , то множество
, то множество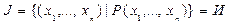
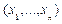 , при которых предикат превращается в истинное высказывание, называется областью истинности данного предиката.
, при которых предикат превращается в истинное высказывание, называется областью истинности данного предиката.

 Пусть предикат Р(x) задан на множестве А. Тогда Р(x) называется тождественно истинным, если его область истинности совпадает с областью определения А, т.е. Р(а) - И при любом значении а Î А.
Пусть предикат Р(x) задан на множестве А. Тогда Р(x) называется тождественно истинным, если его область истинности совпадает с областью определения А, т.е. Р(а) - И при любом значении а Î А.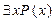 , которое считается истинным тогда и только тогда, когда область истинности предиката Р(х) не пуста. Другими словами, высказывание
, которое считается истинным тогда и только тогда, когда область истинности предиката Р(х) не пуста. Другими словами, высказывание 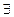 называется квантором существования.
называется квантором существования.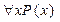 , читается: "Для всех х справедливо Р(x) " или, более кратко: "Для всех х Р(х) ".
, читается: "Для всех х справедливо Р(x) " или, более кратко: "Для всех х Р(х) ".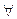 называется квантором общности. Пусть, например, предикат
называется квантором общности. Пусть, например, предикат 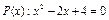 определен на множестве целых чисел Z. Тогда высказывание
определен на множестве целых чисел Z. Тогда высказывание 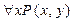 является одноместным предикатом от переменной у. Переменная x в этом предикате уже не играет роли переменной, поскольку истинность предложения
является одноместным предикатом от переменной у. Переменная x в этом предикате уже не играет роли переменной, поскольку истинность предложения 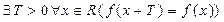
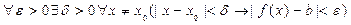
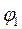 ├ F,...,
├ F,..., 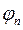 ├ Ф, то
├ Ф, то 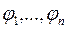 ├ Ф; (Ь) если Ф
├ Ф; (Ь) если Ф ,…, Ф├
,…, Ф├ 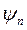 то Ф├
то Ф├ 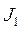 и
и 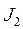 - области истинности, соответственно, предикатов Р(x) и Q{х). Найти область истинности предикатов ØР(х), Р(х) Ú Q(х), Р(х) Ù Q(х), Р(x)®Q(x), Р(х) «Q(х).
- области истинности, соответственно, предикатов Р(x) и Q{х). Найти область истинности предикатов ØР(х), Р(х) Ú Q(х), Р(х) Ù Q(х), Р(x)®Q(x), Р(х) «Q(х). - конечное множество и Р(х) - одноместный предикат, заданный на множестве А. Докажите:
- конечное множество и Р(х) - одноместный предикат, заданный на множестве А. Докажите: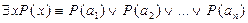 ;
;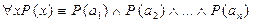 .
.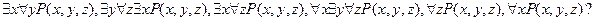

 Какие из предложений, указанных в предыдущей пункте, являются высказываниями?
Какие из предложений, указанных в предыдущей пункте, являются высказываниями?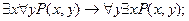

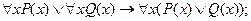
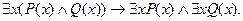
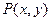 , для которого высказывания
, для которого высказывания 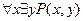 и
и 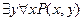 не равносильны.
не равносильны.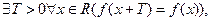 где
где 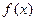 - функция действительного переменного;
- функция действительного переменного;