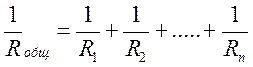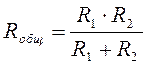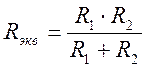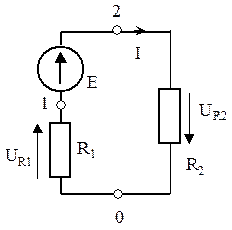Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 20. Законы КирхгофаСодержание книги
Поиск на нашем сайте
а) Первый закон Кирхгофа В любом узле электрической цепи алгебраическая сумма токов равна нулю
где m – число ветвей подключенных к узлу.
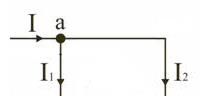
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а: I - I1 - I2 = 0.
Рис.20.1. Токи в узле электрической цепи
б) Второй закон Кирхгофа В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
где n – число источников ЭДС в контуре; Для заданной схемы запишем уравнение по второму закону Кирхгофа:
E = UR + U1.
Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде:
При записи уравнений по второму закону Кирхгофа необходимо: ® задать условные положительные направления ЭДС, токов и напряжений; ® выбрать направление обхода контура, для которого записывается уравнение; ® записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны. Запишем уравнения по II закону Кирхгофа для контуров электрической заданной схемы:
· контур I: E = RI + R1I1 + r0I, · контур II: R1I1 + R2I2 = 0, · контур III: E = RI + R2I2 + r0I. Занятие 21 Способы соединения сопротивлений и расчет эквивалентного
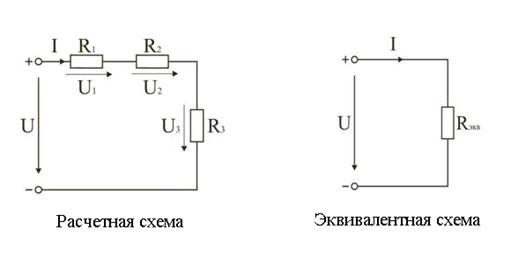
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы, представленной на рисунке, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
а) Электрическая цепь с последовательным соединением элементов
Рис.21.1. Последовательное соединение элементов цепи
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I При последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв. Для заданной схемы: Rэкв = R1 + R2 + R3. В общем случае
Общее сопротивление такой цепи равно:
R общ = R1 + R2 +..... + Rn
Напряжения в такой цепи равны:
Uобщ = U1 + U2 +..... + Un
Токи в такой цепи равны:
I общ = I1 = I2 =......= In б) Электрическая цепь с параллельным соединением элементов
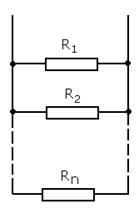
Параллельным соединением резисторов называется такое соединение, при котором начала всех резисторов соединены в одну общую точку, концы резисторов соединены в другую общую точку. Эти точки называются узловыми точками или узлами. Линии цепи между двумя узловыми точками называются ветвями.
Рис.21.2. Параллельное соединение резисторов
Общее сопротивление такой цепи равно:
Для двух резисторов: Напряжения в такой цепи равны: Uобщ = U1= U2=.....= Un Токи в такой цепи равны: I общ = I1+ I2 +.....+ In
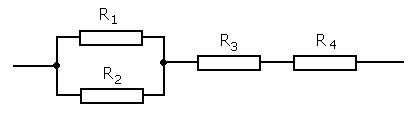
в) Электрическая цепь со смешанным соединением элементов В схемах со смешанным соединением резисторов имеются элементы как последовательного, так и параллельного соединения. (например: см.рис.20..3)
Рис.21. 3. Пример смешанного соединения.
При расчете схем со смешанным соединением необходимо учитывать формат схемы, т.е. каким образом соединены резисторы между собой. Для каждой схемы необходимо составлять свою систему уравнений.
Методика расчета схем смешанного соединения резисторов следующая: - определить наличие и количество контуров с параллельно соединенными резисторами; - определить величину эквивалентного сопротивления каждого из данных контуров; - найти сумму значений эквивалентных сопротивлений и сопротивлений последовательно соединенных резисторов.
Например, имеем схему из трех резисторов. в которой два резистора R1 и R2 включены параллельно, а к ним последовательно подсоединены два резистора R3 и R4.
Расчет произведем следующим образом: Определим эквивалентное сопротивление контура из параллельно соединенных резисторов:
Определим общее сопротивление всей цепи:
R общ = R экв + R 3 + R 4
г) Потенциальная диаграмма неразветвленной электрической цепи Потенциальная диаграмма – график распределения потенциалов вдоль любого участка цепи или контура. При этом по оси абсцисс откладывается сопротивление участков цепи, а по оси ординат – потенциалы между этими участками. Возьмем цепь (см. рис.21.4)
Рис.21.4 Электрическая схема Рис.21.5. Потенциальная диаграмма цепи
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.33.239 (0.007 с.) |

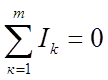
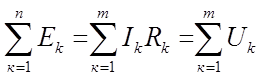
 алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю
алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю