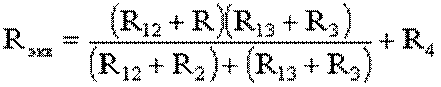Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет разветвленной электрической цепи с несколькими источниками питанияСодержание книги
Поиск на нашем сайте
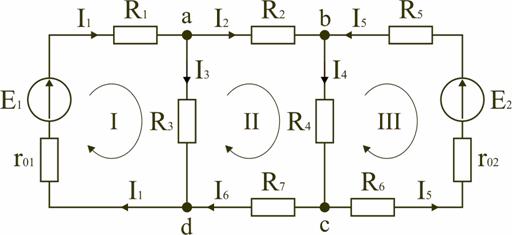
Основным методом расчета является метод непосредственного применения первого и второго законов Кирхгофа. В качестве примера рассмотрим цепь, схема которой приведена на рис. 21.4. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа составляют уравнения для (n–1) узлов. Недостающие m–(n–1) уравнения получают по второму закону Кирхгофа, составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.
Рис. 22.4 1. Обозначение токов во всех ветвях. Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендуются, чтобы направление токов совпадало с направлением ЭДС. 2. Составление уравнений по первому закону Кирхгофа. Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения: узел a: I1 - I2 - I3 = 0; узел b: I2 - I4 + I5 = 0; узел c: I4 - I5 + I6 = 0. 3. Составление уравнений по второму закону Кирхгофа. Необходимо составить 6–3=3 уравнения. В схеме на рис. 21.4 выбираем контура I, II, III и для них записываем уравнения: контур I: E1 = I1(r01 + R1) + I3R3; контур II: 0 = I2R2 + I4R4 + I6R7 - I3R3; контур III: -E2 = -I5(r02 + R5 + R6) - I4R4. 4. Решение полученной системы уравнений и анализ результатов. Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя. 5. Проверка правильности расчетов. Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений: узел d: I3 + I6 - I1 = 0 внешний контур схемы: E1 - E2 = I1(r01 + R1) + I2R2 - I5(r02 + R5 +R6) +I6R7. Независимой проверкой является составление уравнения баланса мощностей с учетом режимов работы элементов схемы с ЭДС:
Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.
в) Соединение элементов электрической цепи по схемам «звезда» и «треугольник» В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 22.5). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 21.6). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
После проведенных преобразований (рис. 22.6) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 22.5)
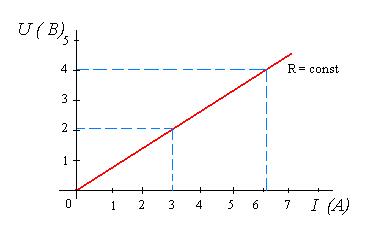
г). Нелинейные элементы электрических цепей. 1) Основные определения В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями (рис. 22.7).
Рис. 22.7 Определим величину линейного сопротивления по характеристике (см. рис. 22.1.)
Таким образом, значение линейного элемента не зависит от изменения напряжения и тока В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения. Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат. Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
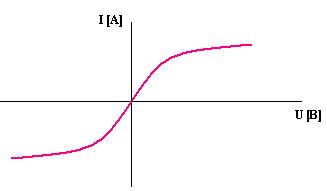
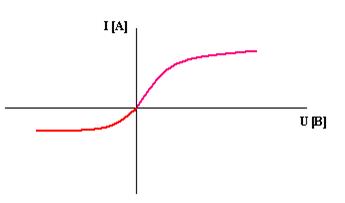
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 22.2), а полупроводниковые диоды - несимметричные характеристики (рис. 22.3).
Рис.22.8. Вольтамперная симметричная характеристика нелинейного элемента
Рис.22.9. Вольтамперная несимметричная характеристика нелинейного элемента
|
|||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.009 с.) |

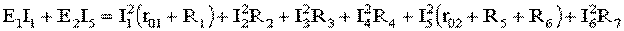 .
. Рис. 21.5
Рис. 21.5
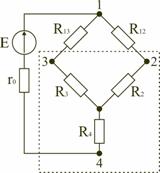 Рис. 21.6
Рис. 21.6
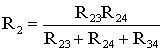 ;
; 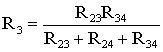 ;
;  .
. ;
; 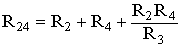 ;
; 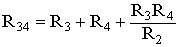 .
.