Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Счетчики со сквозным переносом
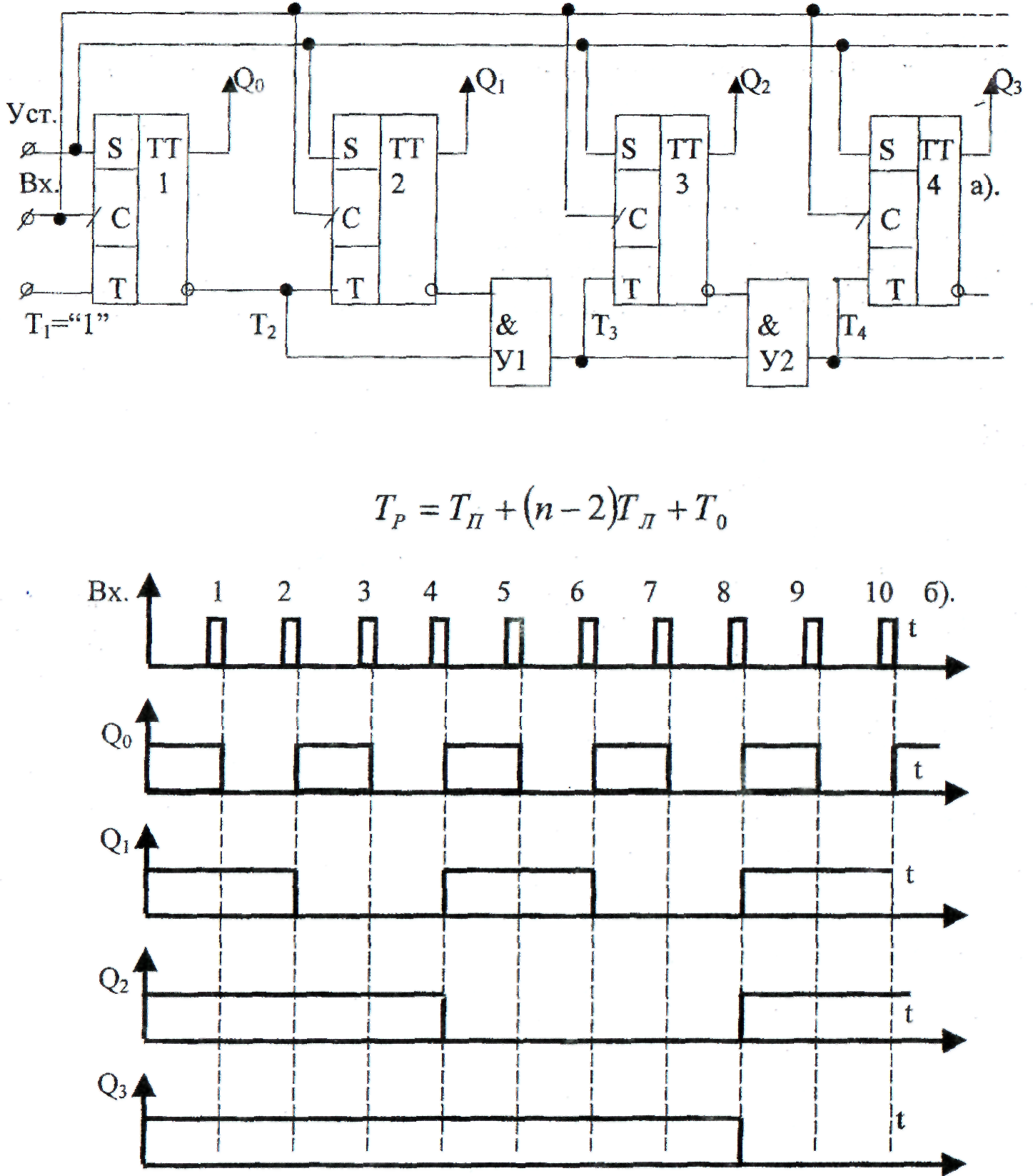
Одной из разновидностей синхронных счетчиков являются счетчики со сквозным переносом. Эти счетчики имеют более высокое быстродействие в сравнении со счетчиками с последовательным переносом, что в не последнюю очередь зависит от реализованного в них принципа передачи информации. На рис. 10.18 приведена схема четырехразрядного двоичного суммирующего счетчика, в котором цепи переноса организованы по принципу сквозной передачи информации. При этом рассматриваемая схема работает следующим образом. Счетные импульсы поступают на тактовые входы С всех триггеров счетчика одновременно, а сигналы сквозного переноса формируются, начиная с его младших разрядов, и поступают на Т - входы триггеров более старших разрядов, выполняя при этом функции сигналов разрешения счета указанными разрядами. Первые два младших разряда схемы рис. 10.18 построены на триггерах ТТ1, ТТ2 аналогично построению 2- разрядной схемы рис. 10.15 и, таким образом, алгоритм их работы совпадает с описанным выше алгоритмом работы указанной схемы. Формирование сигналов переноса в старшие разряды счетчика рис. 10.18 осуществляется как конъюнкция сигналов переноса соответствующего младшего разряда и состояния триггера. В частности, сигнал Т3 переноса в третий разряд счетчика поступает на триггер ТТЗ через логический элемент И (Y 1) в том случае, когда на выходах триггеров младших разрядов ТТ1 и ТТ2 формируются «единичные» сигналы Qo = T 2 =1 и Q 1 =1. Аналогично этому сигнал Т4 переноса в четвертый разряд счетчика реализуется логическим элементом И (Y 2) при формировании «единичных» сигналов во всех предшествующих разрядах счетчика Q 0 = T 2 =1; Q 1 = T 3 =1; Q 2 =1. Таким образом, для сигналов переноса Т3 и Т4 имеем: 48 T 3 = T 2 • Q 1 = Q 0 • Q 1 (10.37) T 4 = T 3 • Q 2 = Q 0 • Q 1 • Q 2 (10.38) В общем случае в счетчиках со сквозным переносом передача информации организуется таким образом, чтобы сигнал переноса j -го разряда определял перенос (f +1)- го разряда. Tj +1 = Tj • Qj -1 (10.39) При этом сигналы переноса формируются начиная с младших разрядов счетчика, а наращивание его разрядности осуществляется подключением необходимого количества триггеров с организацией цепей переноса в соответствии с (10.39). К примеру, в схеме рис. 10.18 для добавления пятого разряда достаточно Т -вход дополнительного (пятого) триггера соединить с выходом Т5 логического элемента Y 3, а входы С и R пятого триггера подключить к шинам тактирования и начальной установки счетчика соответственно.
Рекуррентное соотношение (10.39) при его последовательном раскрытии дает цепочку равенств (10.40), которые удобно использовать при построении счетчиков со сквозным переносом на любое число разрядов. Быстродействие счетчика со сквозным переносом может быть оценено по его времени задержки распространения сигналов, рассчитанному по формуле (10.41). 49 ТР = ТП+(п-2)ТЛ+Т0 (10.41)
где n - число разрядов счетчика; Т П - время переключения одного триггера счетчика; T Л - задержка распространения сигналов в логическом элементе цепи сквозного переноса; Т0 - заданная минимальная длительность каждого состояния счетчика. Для построения вычитающего счетчика со сквозным переносом необходимо поменять направление передачи информации, реализуемое в процессе счета. При этом достаточно перейти к передаче сигналов переноса с инверсных выходов триггеров счетчика, вместо их передачи с прямых выходов, что имело место при построении суммирующих счетчиков. В остальном принцип организации цепей сквозного переноса вычитающего счетчика остается таким же, как и в случае построения суммирующих счетчиков. На рис. 10.19(a) приведена схема 4 - разрядного двоичного вычитающего счетчика со сквозным переносом, а временные диаграммы рис. 10.19(б) иллюстрируют его работу. Формирование сигналов переноса Tj +1 в (j +1) -ый разряд вычитающего счетчика описывается рекуррентным логическим уравнением. Tj +1 = T 1 • где Tj = В схеме рис. 10.19(a) в соответствии с уравнением (10.42) логический элемент Y 1 реализует сигнал переноса T3= T 2 • 50
Рис. 10.19. Вычитающий счетчик числа импульсов со сквозным переносом (а) и временные диаграммы его работы (б).
51
|
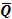 j -1 (10.42)
j -1 (10.42)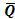 1 =
1 =