
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Асинхронные двоичные счётчики
По способу организации внутренних связей между разрядами (цепи переноса или займа) асинхронные счётчики относят к счётчикам с последовательным переносом. На рис. 10.13 (а) показан трёхразрядный асинхронный двоичный суммирующий счётчик числа импульсов, поступающих на его вход (Вх.Т). Счётчик построен на асинхронных Т - триггерах T 1, T 2 и Т3 с прямым динамическим входом Т. Счётные импульсы поступают на Т - вход первого триггера Т1, который переключается положительным фронтом каждого входного импульса. Переключение второго триггера Т2 осуществляется положительным фронтом сигнала Временные диаграммы рис. 10.13 (б) иллюстрируют изменение состояний на выходах Q 0, Q 1, Q 2 триггеров счётчика Т1,Т2,Т3 во время поступления счётных импульсов. Указанная смена состояний триггеров счётчика рис. 10.13 отображает последовательно возрастающие двоичные числа. В таблице 10.9 переведена последовательность состояний выходов триггеров данного счётчика. Таблица 10.9
40
Анализ таблицы 10.9 показыает, что последовательность состояний счётчика представляет собой возрастающую в пределах данного цикла последовательность двоичных чисел от {000} до {111}. В общем случае число N, записанное в счётчике, определяется соотношением
N = NBX - mK где N вх - число импульсов, поступивших на вход счётчику m =(0,1,2,3,...); m - целое число счетных циклов; К -модуль счёта. Асинхронные счётчики легко наращиваются до любой разрядности подключением к выходу последнего (старшего) разряда нужного числа триггеров. Вместе с тем, с ростам числа разрядов уменьшается быстродействие счётчиков данного типа,так как в них триггеры переключаются последовательно друг за другом. Кроме того, из-за неодновременного тактирования триггеров счётчика на его выходах формируются кратковременно неалгоритмические кодовое комбинации особенно заметшее пра работе на высоких частотах.
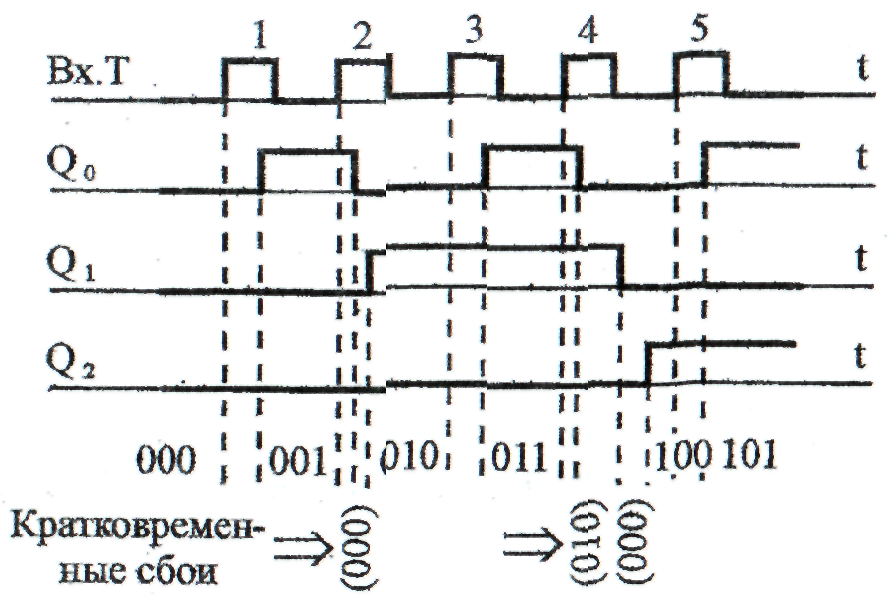
Временные диаграммы рис.10.14, построенные с учётом задержек в переключении триггеров счётчика, иллюстрируют процесс формирования алгоритмических и неалгоритмических состояний асинхронного суммирующего счётчика. В частности, из рис. 10.14 видно, что при поступлении второго счётного импульса вместо кода {010} кратковременно формируется неалгоритмический код {000}, после чего счётчик переключается в алгоритмическое состояние {010}. Четвёртый счётный импульс переводит счетчик в реализуемые одно за другим неалгоритмические состояния {010} и {000} с последующим переходом в алгоритмическое состояние {100}.
42 Из временных диаграмм рис.10.13 (б) и рис.10.14 видна еще одна особенность динамики работы счётчика: его триггеры работают с разной частотой. Наиболее высокую частоту имеет первый триггер, а частота переключения каждого последующего триггера вдвое меньше. Поэтому быстродействие первого триггера в известной мере определяет быстродействие счётчика в целом. Для приведения счётчика рис. 10.13(a) в начальное состояние используется сигнал сброса R (Уст"0"), поступающий одновременно на все R -входы триггеров. Как видно из рис.10.13(a) суммирующий асинхронный счётчик состоит из однотипных асинхронных двоичных суммирующих ячеек Т - типа, построенных, к примеру, на D - триггерах (см. рис.10.13.в). При этом работа суммирующей ячейки, запускаемой положительным фронтом, описывается уравнениями: Q (t +1)= Q (t)
PcdPc = Q (t)· где Рс - сигнал переноса суммирования; Т - сигнал на счётном входе ячейки. В дифференциальной форме данное уравнение имеет вид: dQ (t)= Тогда с учётом (10.31) и (10.32) для функции переноса суммирования Рс имеем: Pc - dPc = Q (t)· dQ (t) =
43 Анализ соотношения (10.34) показывает, что в качестве сигнала переноса Рс можно использовать положительный фронт сигнала на инверсном выходе Pcj -1 = Qj -1 (10.35) Для перехода от построения суммирующего счётчика к построении вычитающего счётчика достаточно в схеме переноса заменить инвертирующий выход Pe j -1 = Qj -1 (10.36) где Рв j -1 - сигнал переноса (займа) вычитания (j -1) - го триггера вычитающего счётчика. Из изложенного следует, что с помощью логических схем, управляющих направлением передачи сигналов переноса, можно легко переходить от схем суммирующих счётчиков к схемам вычитающих счётчиков или наоборот, заменяя в цепях переноса направление передачи сигналов с инверсного (прямого) выхода на их передачу с прямого (инверсного) выхода триггера соответственно. Указанные логические схемы включают между выходами Q и 44
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.105 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
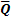 0, формируемого на инверсном выходе триггера T 1 во время формирования отрицательного фронта (среза) сигнала Q 0 на его прямом выходе. Соответственно третий триггер Т3 переключается по положительному фронту сигнала
0, формируемого на инверсном выходе триггера T 1 во время формирования отрицательного фронта (среза) сигнала Q 0 на его прямом выходе. Соответственно третий триггер Т3 переключается по положительному фронту сигнала 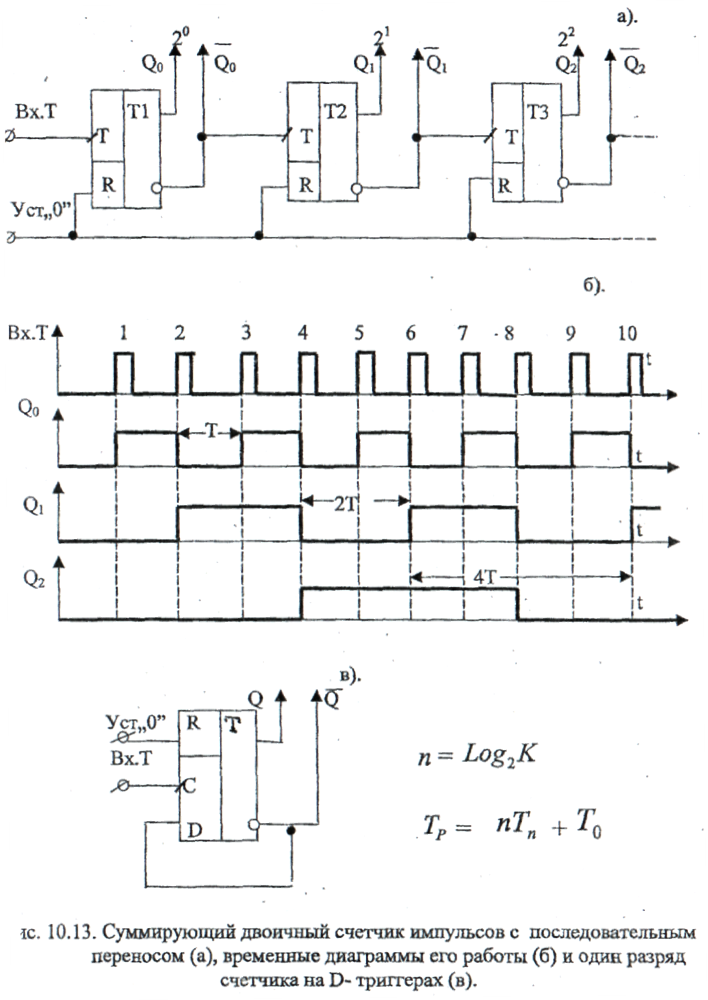
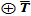 ·dT (10.31)
·dT (10.31)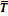 · dT (10.32)
· dT (10.32)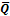 (t)· d
(t)· d 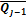 каждого предыдущего триггера со счётным входом последующего триггера
каждого предыдущего триггера со счётным входом последующего триггера 


