
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Причины появления многокритериальностиСодержание книги
Поиск на нашем сайте
как отмечалось выше, всякая модель операции должна иметь единственный критерий. к сожалению, выбор такого критерия часто представляет значительную трудность. поэтому приходится работать с не до конца формализованными моделями, в которых фигурируют несколько показателей, уменьшение или увеличение которых желательно для оперирующей стороны. в таких случаях говорят об исследовании многокритериальных задач. Определение. Многокритериальной задачей называется набор Множество u интерпретируется как множество стратегий оперирующей стороны, а функции gi – как ее критерии. Пример такого рода дает известный лозунг советских времен: «получить максимум продукции при минимуме затрат». Если подходить к этой ситуации формально, легко придти к бессмысленности: свести затраты к нулю нетрудно, но при этом и выпуск продукции будет нулевым, тем не менее, оба показателя, и выпуск продукции, и размер затрат верно отражают стремления оперирующей стороны. При формализации многокритериальных задач в теории исследования операций выделены некоторые часто использующиеся приемы. О них и поговорим, подчеркнем, что выбор такого приема каждый раз должен определяться из содержательного анализа моделируемой операции, тем более, что приведенные ниже примеры далеко не исчерпывают всех возможностей. Причины появления многокритериальности могут быть различными, например, оперирующая сторона может представлять собой группу лиц, каждое из которых имеет, вообще говоря, свои цели. Часто многокритериальность появляется при рассмотрении динамических процессов. Например, если коммерческая фирма стремится к увеличению прибыли, и ее функционирование рассматривается на достаточно длинном временном интервале, то возникает целый ряд показателей, характеризующих прибыль в каждый из моментов времени. Иногда удобно чисто формально рассматривать как многокритериальную задачу обычную модель операции, в которой имеется неопределенный фактор, рассматривая в качестве частных критериев значения общего критерия операции при конкретных значениях неопределенных факторов. В ряде случаев задачу с неопределенными факторами преобразуют в двухкритериальную модель, формулируя задачу минимум и задачу максимум.
Очень часто приходится сталкиваться с ситуацией, когда оперирующая сторона просто не может сформулировать свои предпочтения на вербальном уровне, как в приведенном выше примере. Иногда происходит путаница, и в качестве критерия задаются ограничения, которые должны соблюдаться в данной задаче. Так, например, формулируя задачу на создание межпланетного космического корабля, С.П. Королев писал, что марс должен быть достигнут а) за минимальное время и б) с минимальной затратой средств. Понятно, что если речь идет о пилотируемом полете, то его длительность должна быть не слишком большой (ограничение!). Но вряд ли кто-то станет стремиться к сокращению этого времени на несколько минут, или даже часов, за счет ухудшения других характеристик полета. Отметим, что критерий в любой модели операции должен выражаться через управления оперирующей стороны и, быть может неопределенные факторы. Например, стремление выйти замуж за миллионера может быть лишь благим пожеланием, а не целью, если у оперирующей стороны нет реальных возможностей встретить хотя бы одного миллионера. Точно так же лозунг «наша цель – коммунизм» нельзя рассматривать как формулировку цели операции, поскольку совершенно не ясно, например, ведет ли к достижению этой цели выращивание кукурузы в приполярных районах, или нет. Эти соображения приводят к следующим определениям. Определение. Многокритериальной задачей называется набор Нашей целью будет рассмотрение способов построения на основе многокритериальной задачи Часто такую операцию строят, задавая функцию Примеры сверток По техническим причинам удобно разделить цели операций на два класса: количественные и качественные. К первым относятся те, которые могут быть либо достигнуты, либо нет. Ко вторым – те, степень достижения которых может быть выражена числом. Разумеется, качественная цель может быть описана количественным критерием, который, например, принимает значение 1, если цель достигнута, и значение 0 в противном случае.
Экономический способ свертки. свертка частных критериев g 1,…, gm представляет собой взвешенную сумму В экономических моделях данный способ свертки часто используется при агрегировании абсолютно взаимозаменяемых продуктов. Пример. Предприятие выпускает m видов продукции. критерии g 1,…, gm выражают количества продукции каждого из видов, выпущенных предприятием. доходы предприятия от реализации продукции выражаются сверткой Пример. Рассмотрим деятельность фирмы за m лет. критерии g 1,…, gm выражают прибыль фирмы в соответствующие годы. свертка Пример. В классической биатлонной гонке имеется два критерия: количество промахов g 1 и время прохождения дистанции g 2. Результат спортсмена оценивается по линейной свертке Разбиение на удовлетворительные и неудовлетворительные. пусть имеется количественный критерий g и число g. свертка задает качественный критерий Пример. Знания студента на экзамене оценивается количественным критерием g, принимающим значения от двух до пяти. Качественная цель сдать экзамен описывается критерием Пример. При выборе работы люди часто ориентируются на два критерия: размер заработной платы и удовлетворение от работы. Во многих случаях нет стремления к максимизации заработной платы, гораздо важнее, чтобы она обеспечивала некоторый приемлемый уровень жизни. например, не секрет, что в предперестроечные годы уровень реальных доходов работников торговли заметно превышал аналогичный показатель у врачей, учителей и инженеров, однако, заметного перетока кадров в торговлю не наблюдалось. когда в годы реформ уровень жизни бюджетников заметно упал, многие из них занялись розничной торговлей, чтобы обеспечить себе тот самый приемлемый уровень жизни. Пример. В одной из телевизионных программ 28.11.17 был сформулирован следующий тезис: «женщина должна стремиться к тому, чтобы объем талии не превышал объема бедер». Здесь налицо замена двух количественных критериев (объем талии и объем бедер) одним качественным. Лексикографическая свертка. Пусть даны критерии g 1,…, gm, ранжированные в порядке возрастания номеров. Сначала находятся все точки максимума критерия g 1, из них выбираются те, которые доставляют максимум критерию g 2 и так далее. Наконец, из уже отобранных, выбираются те, которые доставляют максимум критерию gm. Выбранные на последнем этапе стратегии называются точками лексикографического максимума. Пример. При формировании структуры государственных расходов самыми важными являются расходы на государственных служащих, затем идут затраты на оборону, на содержание силовых структур, и так далее. В конце списка обычно оказываются сельское хозяйство и культура. Примерно так на практике формируется расходная часть государственного бюджета. Дизъюнкция. Пусть есть m качественных критериев g 1,…, gm. цель, состоящая в достижении, по крайней мере, одной из частных целей описывается критерием Конъюнкция. Пусть есть m качественных критериев g 1,…, gm. Цель, состоящая в достижении, сразу всех частных целей описывается критерием
Пример. Если за сессию студенту предстоит сдать m экзаменов и каждый из критериев g 1,…, gm описывает сдачу одного из них, то цель, состоящая в успешной сдаче сессии, описывается критерием Отрицание. Пусть имеется качественный критерий g. критерий 1– g описывает цель, состоящую в не достижении исходной. Пример. Если исходная цель g состоит в том, чтобы избежать скандала, то цель, состоящая в попадании в скандальную хронику, описывается критерием 1– g. Обобщенная дизъюнкция. Часто используется следующий способ свертки. Пусть есть m количественных критериев g 1,…, gm. результирующий критерий образуется по правилу Пример. Пусть в шоссейной велогонке принимают участие m спортсменов из одной команды и критерии g 1,…, gm задают места, занятые ее членами. Очень часто все члены команды работают на одного лидера, то есть критерий команды есть Обобщенная конъюнкция. Это свертка, при которой количественные критерии g 1,…, gm заменяются общим критерием В экономических моделях такой способ свертки применяется при агрегировании абсолютно не взаимозаменяемых продуктов. Пример. Пусть для производства изделия требуются комплектующие m видов и количества произведенных деталей описываются числами g 1,…, gm. критерий Пример. По понятным физическим причинам, скорость каравана судов определяется скоростью самого тихоходного судна. Это обстоятельство нашло свое отражение даже в морском уставе. Случайная свертка. В литературе встречается и такой способ свертки критериев. на множестве критериев задается вероятностная мера, и критерий операции выбирается случайным образом в соответствии с этой мерой. понятно, что если при этом оперирующая сторона ориентируется на математическое ожидание, то получается способ свертки, формально совпадающий с экономическим. Приведенные выше примеры являются наиболее простыми, и потому наиболее часто встречающимися. Но, разумеется, бывают и более экзотические способы. Принцип наименьшего сожаления. Это свертка, при которой количественные критерии g 1,…, gm заменяются общим критерием Принцип принятия решений в ЕЭС. По новым законам решение принимается по правилу двойного большинства: решение считается принятым, если за него проголосовало 55% стран население которых составляет 65%. в этом случае можно считать, что имеется столько качественных критериев, сколько стран принимает участие в голосовании. Из них делается два количественных критерия, которые в свою очередь сворачиваются в один качественный.
Старый способ судейства в фигурном катании. Каждый из девяти судей выставлял две оценки от 0 до 6.0 (с шагом 0.1). Затем все участники ранжировались в соответствии с суммой этих оценок (в случае равенства сумм выше ставился участник, у которого выше оценка за артистизм). затем вычислялась сумма мест за выполнение данной программы (короткой или произвольной). Потом участники ранжировались в соответствии с взвешенной суммой показателей за короткую и произвольную программу, что и давало результирующее место участника. Способ судейства в прыжках в длину. Сравнение результатов двух участников производится по самому дальнему прыжку каждого из них. Если эти прыжки одинаковы, то во внимание принимается следующий по дальности и так далее. Лексимин. Во многих социальных моделях и в теоретической математике полезен следующий способ свертки. При сравнении двух решений многокритериальной задачи прежде всего сравниваются самые маленькие значения критериев (возможно, свои у каждого варианта). Если они одинаковы, то во внимание принимаются следующие по величине и так далее. Разумеется, не существует и не может существовать идеального способа свертки, пригодного на все случаи жизни. Если уж правилами предусмотрен такой способ подведения итогов, как в предыдущем примере, то в соответствующей модели надо пользоваться именно им. но совсем глупо было бы использовать его в задаче о караване судов. Теорема о свертке Теорема. Пусть каждый из критериев g 1,…, gm принимает лишь два значения 0 и 1, а f:{0,1} m ®{0,1} – произвольная функция. тогда критерий g,определенный условием g (u) = f (g 1(u),…, gm (u)), может быть выражен через следующие элементарные операции: 1. конъюнкция: g 1,…, gm ® 2. дизъюнкция: g 1,…, gm ® 3. отрицание: gi ® 1– gi. Доказательство. Пусть y =(y 1,…, ym) – произвольный булев вектор размерности m (здесь yi равны 0 или 1 при любом i = 1,…, m). рассмотрим функцию fy:{0,1} m ®{0,1}, определенную условием Пример. На референдуме о сохранении союза советских социалистических республик гражданам предлагалось ответить на четыре вопроса. Власти предлагали своим сторонникам ответить «да, да, нет, да». таким образом, есть, четыре вспомогательных качественных критерия gi (ответ на i -ый вопрос). Если общая цель g состоит в лояльности власти, то она выражается через частные с помощью свертки g = g 1 g 2(1– g 3) g 4. Для заданной нам функции f, обозначим y ={ y: f (y)=1}. Покажем, что интересующий нас критерий g представляется в виде
В самом деле, если g (u)=1, то по определению вектор t =(g 1(u),…, gm (u)) принадлежит множеству y. значит, произведение в формуле (28) содержит множитель (1– fy (g 1(u),…, gm (u))), равный нулю. следовательно, и все произведение равно нулю, а вся правая часть формулы (28) равна 1.
Если же g (u)=0, то вектор t =(g 1(u),…, gm (u)) не принадлежит множеству y, и для всех y Î y имеем fy (g 1(u),…, gm (u))=0. значит, для этого u все сомножители в формуле (28) равны 1, а тогда и произведение в правой части равенства (28) равно 1, а сама правая часть равна нулю. Для завершения доказательства остается заметить, что при построении функций fy мы пользовались лишь операциями отрицания и конъюнкции, а в формуле (28) использовалась еще и дизъюнкция. Замечание. Легко видеть, что сама операция дизъюнкции может быть выражена через конъюнкцию и отрицание, то есть список «элементарных» операций может быть сокращен. Теорема. Пусть каждый из критериев g 1,…, gm принимает лишь конечное число значений, а 1. экономическая свертка: g 1,…, gm ® 2. разбиение на удовлетворительные и неудовлетворительные: gi ® 3. конъюнкция: g 1,…, gm ® 4. дизъюнкция: g 1,…, gm ® 5. отрицание: gi ® 1– gi. Доказательство. Значения, которые может принимать критерий gi, обозначим в порядке возрастания символами 1. для каждого i = 1,…, m и каждого 2. верно и обратное: критерий gi может быть представлен как функция критериев
где положено в самом деле, если 3. рассмотрим вспомогательные критерии g g(u), определенные условиями
(здесь 4. тогда по условию теоремы, тогда критерий 5. но каждый из критериев g g и 6. аналогично формуле (29) доказывается равенство
Для завершения доказательства остается заметить, что критерии Примеры Пример. Пусть каждый из критериев g 1,…, gm принимает лишь конечное число значений. Значения, которые может принимать критерий gi, обозначим в порядке возрастания символами очевидно, что результирующий критерий может принимать лишь конечное число значений вида используя разбиение на удовлетворительные и неудовлетворительные. Тогда Пример. Пусть каждый из критериев g 1,…, gm принимает лишь конечное число значений. значения, которые может принимать критерий gi, обозначим в порядке возрастания символами Очевидно, что результирующий критерий может принимать лишь конечное число значений вида Используя разбиение на удовлетворительные и неудовлетворительные. тогда Пример. Пусть каждый из критериев g 1,…, gm принимает лишь конечное число значений. значения, которые может принимать критерий gi, обозначим в порядке возрастания символами Пусть ОПТИМАЛЬНОСТЬ ПО ПАРЕТО Вильфредо Парето (1848–1923) – итальянский экономист. Определение. Будем говорить, что стратегия u Î u доминирует (по Парето) стратегию v Î u, а соответствующий вектор выигрышей (g 1(u),…, gm (u)) доминирует вектор (g 1(v),…, gm (v)), если для всех i = 1,…, m выполняются неравенства gi (u)³ gi (v), а для некоторого k выполняется строгое неравенство gk (u)> gk (v). Определение. Стратегия u Î u, и соответствующий вектор выигрышей (g 1(u),…, gm (u)) называются эффективными (оптимальными по Парето), если не существует стратегии v Î u, которая доминировала бы стратегию u. Полезно иметь в виду следующую геометрическую интерпретацию данного определения. Вектор выигрышей (g 1(v),…, gm (v)) является эффективным, если пересечение множества всех возможных векторов выигрышей Множество эффективных векторов выигрышей, вообще говоря, не выпукло. Пример. Пусть Множество эффективных векторов может быть и не замкнутым. Пример. Пусть Эффективное множество в этой задаче состоит из двух дуг и одной точки Отсюда, следует, что не существует такой непрерывной функции Приведенные примеры показывают, что нетривиальной становится даже постановка задачи о поиске эффективных точек, коль скоро речь идет о задаче полного выбора, что часто бывает нужно на практике. В самом деле, в общем, не ясно даже в каких терминах должен быть сформулирован ответ в этой задаче. По этой и некоторым другим причинам технически удобнее бывает работать со слабо эффективными точками, хотя они менее интересны в прикладном плане. Определение. Стратегия u Î u, и соответствующий вектор выигрышей (g 1(u),…, gm (u)) называются слабо эффективными, если не существует стратегии v Î u, которая сильно доминировала бы стратегию u. Лемма. Пусть множество u компактно, а функции Доказательство. Пусть точка v не является слабо эффективной. Тогда найдется такая точка u, что выполняются неравенства Но это означает, что его дополнение, множество эффективных точек, является замкнутым. Замкнутое подмножество компактного множества компактно, поэтому компактно множество слабо эффективных стратегий. образ компактного множества компактно, следовательно, компактно множество слабо эффективных векторов выигрышей. Пусть множество u компактно, а функции
Лемма. Всякая точка из множества um является эффективной. Доказательство. Допустим противное. Пусть точка v Î u доминирует точку u. тогда найдется такой номер k, что Следствие. Пусть множество u компактно, а функции Доказательство. В силу теоремы Вейерштрасса, непрерывная функция g 1 достигает своего максимума на компактном множестве u 0, то есть множество u 1 не пусто. Множество u 1 замкнуто, так как является прообразом компактного множества (точки действительно прямой) при непрерывном отображении g 1. Замкнутое множество u 1 является подмножеством компактного множества u 0. поэтому u 1 компактно. По аналогичным соображениям множество u 2 не пусто и компактно. продолжая те же рассуждения, приходим к выводу, что множество um не пусто. Любая его точка эффективна, что и доказывает следствие.
ПОИСК ЭФФЕКТИВНЫХ ТОЧЕК Пусть u – компактное множество, а g 1,…, gm – непрерывные функции, Теорема (Гермейер). Пусть u 0 – эффективная точка, причем gi (u 0)>0 для всех i = 1,…, m. Тогда существуют положительные числа l1,…l m такие, что Доказательство. Положим Остается положить К сожалению, нельзя утверждать, что всякая точка максимума функции Пример.Пусть u ={(u 1, u 2): 0£ u 1£1, 0£ u 2£1}, g 1(u)= u 1, g 2(u)= u 2. при Теорема.Пусть существуют такие положительные числа Доказательство. Допустим противное. Тогда найдется такая точка u 1, что Пусть теперь множество u выпукло, а функции g 1,…, gm вогнуты. Теорема (Карлин).Пусть x 0 – эффективная точка. Тогда существуют неотрицательные числа p 1,…, p m такие, что Доказательство. Не ограничивая общности, можем считать, что gi (u)>0 для всех i = 1,…, m. В силу теоремы Гермейера существуют положительные числа Тогда (u 0, f (u 0)) является решением задачи математического программирования
В силу теоремы Куна–Такера найдутся такие неотрицательные числа a i, i = 1,…, m, для которых (u 0, f (u 0)) будет точкой максимума функции
на множестве
а тогда u 0 является точкой максимума функции Остается заметить, что в силу равенства (30), по крайней мере, одно a i не равно нулю. Тогда мы можем положить Теорема. Пусть существуют положительные числа p 1,…, p m такие, что Доказательство. Допустим противное. Тогда найдется такая точка u 1, что gi (u 1)³ gi (u 0) для всех i =1,…, m, причем, по крайней мере, одно из этих неравенств не обращается в равенство. Умножая эти неравенства на pi и суммируя, получим неравенство F(u 1)>F(u 0), что противоречит условию. Нельзя утверждать, что всякая эффективная точка может быть найдена в результате максимизации функции Пример. Пусть С другой стороны, при неотрицательных коэффициентах p 1,…, pm, точка максимума функции Пример. Пусть Теорема. Пусть существуют неотрицательные числа p 1,…, p m такие, что Доказательство. Допустим противное. тогда найдется такая точка u 1, что Примеры Пример. Пусть множество u представляет собой стандартный симплекс u ={(u 1, u 2, u 3): u 1³0, u 2³0, u 3³0, u 1+ u 2+ u 3=1} и имеется два критерия g 1(u)=2 u 1+7 u 2+ u 3 и g 2(u)=3 u 1+ u 2+4 u 3. Найдем точки максимума функции F(u)= pg 1(u)+(1– p) g 2(u). Так как критерии в данной задаче линейны, а максимум линейной функции непременно достигается в одной из вершин, то Пример. Пусть множество u представляет собой стандартный симплекс u ={(u 1, u 2, u 3): u 1³0, u 2³0, u 3³0, u 1+ u 2+ u 3=1} и имеется два критерия g 1(u)=3 u 1+7 u 2+ u 3 и g 2(u)=4 u 1+ u 2+4 u 3. Анализ показывает, что в данном случае эффективными являются все точки, лежащие на двух ребрах: соединяющем вершину (1,0,0) с вершиной (0,1,0) и соединяющем вершины (1,0,0) и (0,0,1). В этом случае множество эффективных точек не выпукло. В двух предыдущих примерах полезно нарисова
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.60 (0.011 с.) |

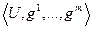 , где u – множество, а
, где u – множество, а 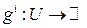 (i =1,…, m) – функции.
(i =1,…, m) – функции.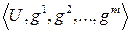 , где u – множество, а gi – функции, отображающие u во множество действительных чисел
, где u – множество, а gi – функции, отображающие u во множество действительных чисел  .
.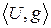 .
.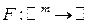 , и полагая, что
, и полагая, что 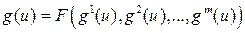 . функцию f в таком случае называют функцией свертки (или просто сверткой) критериев.
. функцию f в таком случае называют функцией свертки (или просто сверткой) критериев.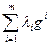 .
.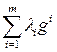 . коэффициенты свертки в этом случае имеют смысл цен.
. коэффициенты свертки в этом случае имеют смысл цен.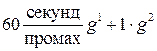 (если время измерять в секундах).
(если время измерять в секундах).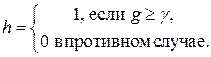
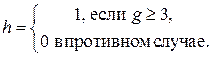
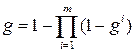 .
.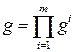 .
.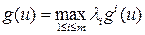 .
.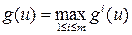 .
.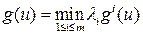 .
.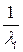 имеют при этом смысл количества деталей i -го вида, необходимых для сборки одного готового изделия.
имеют при этом смысл количества деталей i -го вида, необходимых для сборки одного готового изделия.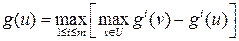 , который нужно минимизировать.
, который нужно минимизировать.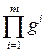 ;
;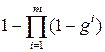 ;
;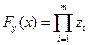 , где zi = xi, если yi =1, и zi =1– xi, если yi =0. непосредственно проверяется, что fy (y)=1, и fy (x)=0 для любого x ¹ y.
, где zi = xi, если yi =1, и zi =1– xi, если yi =0. непосредственно проверяется, что fy (y)=1, и fy (x)=0 для любого x ¹ y.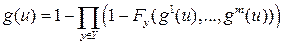 . (28)
. (28)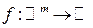 – произвольная функция. Тогда критерий g,определенный условием g (u) = f (g 1(u),…, gm (u)), может быть выражен через следующие элементарные операции:
– произвольная функция. Тогда критерий g,определенный условием g (u) = f (g 1(u),…, gm (u)), может быть выражен через следующие элементарные операции: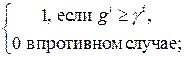
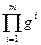 ;
;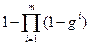 ;
;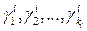 . при сформулированных условиях критерий g может тоже принимать лишь конечное число значений. Обозначим их в порядке возрастания символами
. при сформулированных условиях критерий g может тоже принимать лишь конечное число значений. Обозначим их в порядке возрастания символами 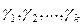 . дальнейшие рассуждения разобьем на шесть шагов.
. дальнейшие рассуждения разобьем на шесть шагов.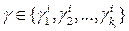 с помощью элементарной операции второго типа образуем вспомогательный критерий
с помощью элементарной операции второго типа образуем вспомогательный критерий 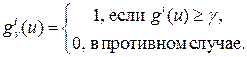 . разумеется, критерий
. разумеется, критерий 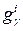 может быть выражен как функция критерия gi.
может быть выражен как функция критерия gi.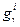 . чтобы убедиться в этом, заметим, что
. чтобы убедиться в этом, заметим, что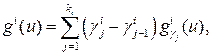 (29)
(29)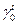 =0.
=0.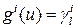 , то для всех j > l справедливо равенство
, то для всех j > l справедливо равенство 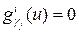 , а для всех j ≤ l будем иметь
, а для всех j ≤ l будем иметь 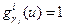 . поэтому для такого u правая часть равенства (29) может быть переписана в виде
. поэтому для такого u правая часть равенства (29) может быть переписана в виде 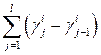 . эта сумма, очевидно, равна
. эта сумма, очевидно, равна 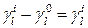 , то есть равенство (29) справедливо.
, то есть равенство (29) справедливо.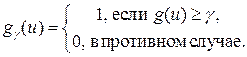
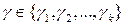 ). Каждый из этих критериев является функцией критерия g.
). Каждый из этих критериев является функцией критерия g.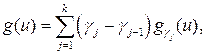 где g0=0.
где g0=0.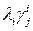 . обозначим их в порядке возрастания
. обозначим их в порядке возрастания 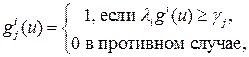
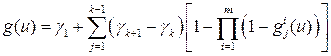 .
.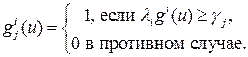
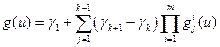 ..
..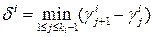 и
и 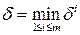 . обозначим
. обозначим 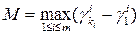 и положим
и положим 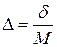 . нужный нам критерий задается экономической сверткой
. нужный нам критерий задается экономической сверткой 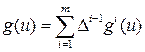 .
.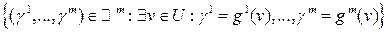 и конуса
и конуса 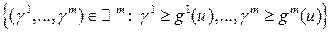 состоит из одной точки (g 1(v),…, gm (v)).
состоит из одной точки (g 1(v),…, gm (v)).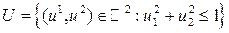 , g 1(u)= u 1, g 2(u)= u 2. Множество эффективных векторов в этой задаче представляет собой четверть окружности
, g 1(u)= u 1, g 2(u)= u 2. Множество эффективных векторов в этой задаче представляет собой четверть окружности 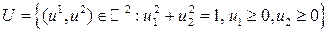 и, следовательно, не выпукло.
и, следовательно, не выпукло.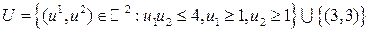 ,
, 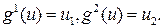
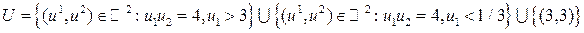 . это множество не замкнуто, поскольку точки (3,1/3) и (1/3,3) являются предельными для него, но не доминируются точкой (3,3).
. это множество не замкнуто, поскольку точки (3,1/3) и (1/3,3) являются предельными для него, но не доминируются точкой (3,3).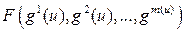 совпадает с множеством эффективных точек в многокритериальной задаче
совпадает с множеством эффективных точек в многокритериальной задаче 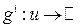 непрерывны. Тогда множество слабо эффективных стратегий компактно.
непрерывны. Тогда множество слабо эффективных стратегий компактно.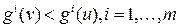 в силу непрерывности функций gi найдется настолько малая окрестность o точки v, что неравенства
в силу непрерывности функций gi найдется настолько малая окрестность o точки v, что неравенства 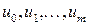 . Положим
. Положим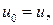
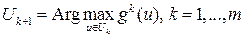 .
.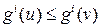 для i =1,…, k –1, и gk (u)< gk (v). Так как точка u Î u 1, выполняется неравенство g 1(u)³ g 1(v), то есть на самом деле g 1(u)= g 1(v) и, следовательно, v Î u 1. Но тогда в силу включения u Î u 2, имеем g 2(u)³ g 2(v). Продолжая эти рассуждения, получим v Î uk. но тогда справедливо неравенство gk (u)³ gk (v), которое противоречит условию gk (u)< gk (v). Полученное противоречие доказывает лемму.
для i =1,…, k –1, и gk (u)< gk (v). Так как точка u Î u 1, выполняется неравенство g 1(u)³ g 1(v), то есть на самом деле g 1(u)= g 1(v) и, следовательно, v Î u 1. Но тогда в силу включения u Î u 2, имеем g 2(u)³ g 2(v). Продолжая эти рассуждения, получим v Î uk. но тогда справедливо неравенство gk (u)³ gk (v), которое противоречит условию gk (u)< gk (v). Полученное противоречие доказывает лемму.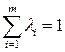 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 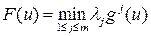 .
.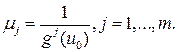 Тогда
Тогда 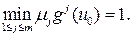 Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, m i gi (u)£1. значит,
Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, m i gi (u)£1. значит, 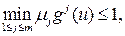 а это означает, что u 0 – одна из точек максимума функции
а это означает, что u 0 – одна из точек максимума функции 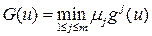 .
.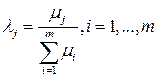 и заметить, что тогда u 0 – одна из точек максимума функции f (u). Теорема доказана.
и заметить, что тогда u 0 – одна из точек максимума функции f (u). Теорема доказана.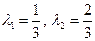 точки максимума функции
точки максимума функции 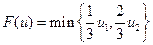 образуют отрезок {(u 1, u 2): u 1=1, 0.5£ u 2£1}, но только одна его точка (1,1) является эффективной.
образуют отрезок {(u 1, u 2): u 1=1, 0.5£ u 2£1}, но только одна его точка (1,1) является эффективной.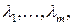 что
что 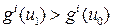 для всех i =1,…, m. но тогда
для всех i =1,…, m. но тогда 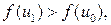 что противоречит условию.
что противоречит условию.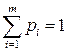 и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 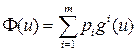 .
.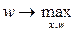 ,
, 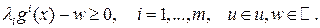
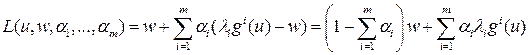
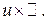 , но это возможно, только если
, но это возможно, только если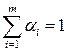 , (30)
, (30)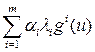 .
.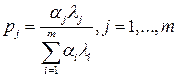 .
.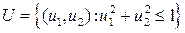 ,
, 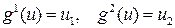 . Максимум функции
. Максимум функции 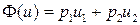 достигается в точке
достигается в точке 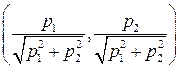 . в то же время, точка (1, 0) является эффективной.
. в то же время, точка (1, 0) является эффективной.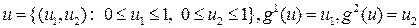 Точки максимума функции F(u)=1× g 1(u)+0× g 2(u) образуют отрезок {(u 1, u 2): u 1=1, 0£ u 2£1}, а эффективной является только одна точка (1,1) этого отрезка.
Точки максимума функции F(u)=1× g 1(u)+0× g 2(u) образуют отрезок {(u 1, u 2): u 1=1, 0£ u 2£1}, а эффективной является только одна точка (1,1) этого отрезка.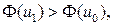 что противоречит условию.
что противоречит условию.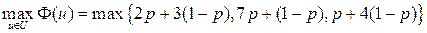 . Нарисовав графики, нетрудно понять, что при 0£ p £1/3 максимум достигается в вершине (0,1,0), а при 1/3£ p £1 он достигается в вершине (0,0,1). При p =1/3 точки максимума заполняют все ребро, соединяющие эти вершины. Таким образом, все точки этого ребра являются эффективными.
. Нарисовав графики, нетрудно понять, что при 0£ p £1/3 максимум достигается в вершине (0,1,0), а при 1/3£ p £1 он достигается в вершине (0,0,1). При p =1/3 точки максимума заполняют все ребро, соединяющие эти вершины. Таким образом, все точки этого ребра являются эффективными.


