Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод ветвей и границ решения задач целочисленного программирования ⇐ ПредыдущаяСтр 10 из 10
Методом ветвей и границ удобно решать такие задачи целочисленного программирования, в которых число неизвестных невелико либо требования целочисленности относятся не ко всем неизвестным. Суть метода ветвей и границ состоит в том, что для тех неизвестных, к которым относится требование целочисленности, нужно определить границы, в которых могут находиться значения этих неизвестных. Затем решаются соответствующие задачи линейного программирования. Задание границ, в которых должны находиться значения неизвестных в задаче целочисленного программирования, можно записать так: На практике во многих случаях границы значений неизвестных уже включены в систему ограничений задачи целочисленного программирования или же их можно определить исходя из экономического содержания задачи. Иначе можно принять, что нижняя граница Как метод ветвей и границ позволяет уточнить границы допустимых значений неизвестных? Сначала решается, допустим, симплекс-методом задача линейного программирования, соответствующая задаче целочисленного программирования. Пусть найден оптимальный план в этой задаче и значением какой-либо его координаты Обозначим целую часть координаты В другой новой задаче линейного программирования верхней границей значения координаты Таким образом, от первой задачи линейного программирования "ответвились" две новые задачи, в которых в которых изменились границы допустимых значений одной неизвестной. При решении каждой из этих задач возможны три случая: · оптимальный план не является целочисленным, · оптимальный план является целочисленным, · задача не имеет решений. Лишь в первом случае возможно "ответвление" новых задач способом, показанным выше. Во втором и третьем случае "ветвление" прекращается.
На каждой итерации решения задачи целочисленного программирования решается одна задача. Введём понятие: список решаемых задач линейного программирования. Из списка следует выбрать задачу, решаемую на соответствующей итерации. На дальнейших итерациях список меняется, так как решённые задачи в него уже не входят, а вместо них в список включаются новые задачи, которые "ответвились" от предыдущих задач. Для того, чтобы ограничить "ветвления", то есть уменьшить число решаемых задач, на каждой итерации следует определить нижнюю границу максимального значения целевой функции. Это делается следующим образом: · если задача задана в нормальной форме, то перед её решением нижняя граница имеет значение нуль (то есть · если на некоторой итерации (назовём её p -й) найденный план не является целочисленным и максимальное значение целевой функции больше ранее установленной нижней границы, то на следующей итерации нижняя граница максимального значения целевой функции остаётся прежней (как на предыдущей итерации, то есть · если на некоторой итерации найденный план · если на некоторой итерации максимальное значение целевой функции, найденное вместе с этим планом Согласно алгоритму решения задачи целочисленного программирования методом ветвей и границ, на каждой p -й итерации требуется сделать 4 шага. · Шаг 1. Если в списке решаемых задач нет ни одной задачи, то задача целочисленного программирования решена. Максимальное значение функции цели - то, которое было найдено на предыдущей итерации, оптимальный план - целочисленный план, найденный на предыдущей итерации. В противном случае следует выбрать одну из задач, имеющихся в списке. · Шаг 2. Решается выбранная из списка задача линейного программирования. Если задача не имеет решения или для полученного на этом шаге оптимального плана
· Шаг 3. Если найденный оптимальный план · Шаг 4. Выбрать любую дробную координату оптимального плана Пример. Решить методом ветвей и границ следующую задачу целочисленного программирования. Найти максимум целевой функции
Решение. Допустим, что заданы или определены следующие границы оптимальных значений неизвестных:
Так как задача задана в нормальной форме, она имеет целочисленный план В списке решаемых задач - 1-я задача:
Итерация 1. Шаг 1. С помощью симплекс-метода получено решение 1-й задачи:
Так как найденный план не является целочисленным, следует шаг 4. Шаг 4. Так как оптимальный план Итак, следует решить 2-ю задачу:
и 3-ю задачу:
Нижняя граница максимального значения целевой функции Итерация 2. Шаг 1. Из списка решаемых задач выбираем 2-ю задачу. Шаг 2. Констатируем, что 2-я задача не имеет решения, так как её система ограничений несовместна. Тогда Итерация 3. Шаг 1. В списке имеется только одна - 3-я задача. Шаг 2. Применяя симплекс-метод, получаем решение 3-й задачи:
Так как это решение не является целочисленным, следует шаг 4. Шаг 4. Выбираем дробную координату 4-я задача:
5-я задача:
Нижняя граница максимального значения функции цели Итерация 4. Шаг 1. Из списка решаемых задач, в котором имеются 4-я и 5-я задачи, выбираем 4-ю задачу. Шаг 2. Применяя симплекс-метод, получаем решение 4-й задачи:
Так как полученное решение не является целочисленным, следует шаг 4. Шаг 4. Выбираем дробную координату 6-я задача:
7-я задача:
Итак, в списке решаемых задач имеются 5-я, 6-я и 7-я задачи, а нижняя граница максимального значения функции цели Итерация 5. Шаг 1. Из списка выбираем 5-ю задачу. Шаг 2. Применяя симплекс-метод, получаем решение 5-й задачи:
Так как найденный план не является целочисленным, следует шаг 4. Шаг 4. Выбираем дробную координату 8-я задача:
9-я задача:
В списке решаемых задач имеются 6-я, 7-я, 8-я и 9-я задачи, а нижняя граница максимального значения функции цели
Итерация 6. Шаг 1. Из списка решаемых задач выбираем 6-ю задачу. Шаг 2. Констатируем, что 6-я задача не имеет решения. Поэтому нижняя граница максимального значения функции цели Итерация 7. Шаг 1. Из списка решаемых задач выбираем 7-ю задачу. Шаг 2. Применяя симплекс-метод, получаем решение 7-й задачи:
Шаг 3. Так как полученное решение является целочисленным, то нижняя граница максимального значения функции цели Итерация 8. Шаг 1. Из списка решаемых задач выбираем 8-ю задачу. Шаг 2. Применяя симплекс-метод, получаем решение 8-й задачи:
Нижняя граница максимального значения функции цели Итерация 9. Шаг 1. В списке решаемых задач имеется лишь 9-я задача. Шаг 2. Применяем симплекс-метод и получаем решение 9-й задачи:
Шаг 3.Так как полученное решение является целочисленным, нижняя граница максимального значения функции цели Итерация 10. Шаг 1. В списке решаемых задач нет ни одной задачи. Таким образом, решение данной задачи целочисленного программирования следующее:
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ Нелинейное программирование – раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. К нелинейному программированию относят квадратичное, дробное, выпуклое, дискретное, целочисленное и геометрическое программирование. В общем виде задачу нелинейного программирования можно сформулировать так:
при условии
где х – вектор искомых переменных; F (х) - целевая числовая функция; g (x) – вектор-функция системы ограничений. При этом могут быть разные случаи: 1) целевая функция – нелинейная, а ограничения – линейны; 2) целевая функция – линейная, а ограничения (хотя бы одно из них) – нелинейные; 3) целевая функция и ограничения нелинейные. Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях (32) имеют место: а) знаки равенства; б) знаки неравенства. Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.
При решении некоторых нелинейных задач иногда удается использовать линейную теорию. Для этого вводят допущение, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению переменных. Такой подход называется методом кусочно-линейных приближений. Среди большого числа вычислительных алгоритмов нелинейного программирования значительное место занимают: - различные варианты градиентных методов (метод проекции градиента, метод условного градиента и т. п.); - методы штрафных функций; - методы барьерных функций; - метод модифицированных функций Лагранжа и др. Нелинейные задачи с ограничениями в форме равенств нередко решаются с помощью введения функции Лагранжа: где L (x, λ) - лагранжиан; φ(x) - целевая функция; λ i (i = 1, 2,..., k) – множители Лагранжа; k - число ограничений gi (x). Универсального метода, позволяющего находить наиболее эффективным способом решение любой нелинейной задачи, не существует. Поэтому для каждой конкретной задачи, учитывая ее специфику, подбирают тот или иной наиболее подходящий метод (и алгоритм) решения. Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров. Хорошо известно, что чем больше партия закупаемого товара, тем меньше стоимость единицы продукта. Каждому знакомо понятие розничных и оптовых цен.
Метод Фибоначчи Этот метод является более эффективным по сходимости, чем метод дихотомии, и обладает наибольшей скоростью сходимости для класса непрерывных функций. В нем, как и в методе «золотого сечения», на каждом шаге производится только одно определение целевой функции, а в методе дихотомии два. Но в этом методе требуется заранее выбрать число испытаний N. Метод основан на использовании чисел Фибоначчи для нахождения точек, в которых определяется целевая функция F (х). Числа Фибоначчи образуют последовательность целых чисел так, что Первые 15 чисел Фибоначчи.
В основу схемы поиска экстремума положены два исходных соотношения LN -2 = LN -1 + LN, при N 3, и Первое из них связывает длины трех соседних (по номерам) интервалов неопределенности. Второе требует, чтобы процесс поиска экстремума всегда завершался одинаково: симметричным размещением двух последних точек (хN -1 и хN) на интервале LN -1. Координаты точек, в которых определяются целевые функции, находятся по формулам:
где r – номер шага (r = 0, 1, 2, 3, …, N –3);
ar, br – начало и конец r -го интервала неопределенности. Алгоритм метода является итерационной процедурой, включающей следующие этапы. На первом этапе, который соответствует первому шагу поиска (
В этих точках определяется целевая функция и в зависимости от ее значений выбирается новый (суженный) интервал неопределенности. Второй этап включает в себя (N –3) итерационных шагов. На каждом r -ом шаге в интервале неопределенности lr, полученном на предыдущем шаге, рассматривается новая пара испытаний Особенностью данного алгоритма поисковой оптимизации является то, что из двух точек Третий этап характерен тем, что после проведения (N –1)-го испытания необходимо решить, по какую сторону от точки х, находящейся внутри интервала неопределенности lN -1, лежит точка истинного экстремума. Для этого последнее N -е испытание проводится вблизи от точки предыдущего испытания в точке (х) или (e – х), что позволяет определить апостериорный (послеопытный) интервал неопределенностиe + lN. На рис. 10 приведена схема поиска экстремума по методу Фибоначчи (второй и третий этапы). В заключение данного раздела проведем сравнение методов «золотого сечения» и Фибоначчи. Метод Фибоначчи более эффективен по сходимости, т.е. по достижению необходимого сужения интервала неопределенности при одинаковом числе определений целевой функции. Но его недостатки: 1. Заранее заданное число испытаний, которое нельзя менять в процессе сужения интервала неопределенности, и если после N испытаний не получена нужная точность определения оптимума, то все приходится начинать сначала, задавшись большим N. 2. При применении ЭВМ необходимо запоминать (или каждый раз вычислять) числа Фибоначчи.
Рисунок 10. Метод «золотого сечения» не требует заранее заданного числа испытаний. Для него требуется сравнительно небольшой объем памяти ЭВМ, и он прост в реализации. С точки зрения эффективности метод «золотого сечения» занимает промежуточное положение между методами дихотомии и Фибоначчи. На практике иногда комбинируют оба метода: первые шаги делают по методу «золотого сечения», а затем, когда оптимум достаточно близок, фиксируют число N и переходят к методу Фибоначчи. СПИСОК ЛИТЕРАТУРЫ 1. Аоки М. Введение в методы оптимизации / М. Аоки - М.: Наука, 2017. - 334 с. 2. Ашманов С.А. Линейное программирование. Учебное пособие / С.А. Ашманов - М.: Наука, 1981. - 340 с. 3. Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. / Б. Банди - М.: Радио и связь,2008. - 128с. 4. Васильев Ф.П. Численные методы решения экстремальных задач. Учебное пособие / Ф.П. Васильев - М.: Наука, 1958. - 549 с. 5. Дегтярев Ю.И. Методы оптимизации: Учебное пособие для вузов / Ю.И. Дегтярев - М.: Сов. Радио, 1980. - 272 с. 6. Карманов В.Г. Математическое программирование. Учебное пособие / В.Г. Карманов - М.: Наука, 2016. - 285 с. 7. Моисеев Н.Н. Методы оптимизации. Учебное пособие / Н.Н. Моисеев, Ю.П. Иванилов, Е.М. Столярова - М.: Наука, 2018. - 351 с. 8. Моисеев Н.М. Методы оптимизации / Н.М. Моисеев - М.: Наука, 1978. - 351с. 9. Поляк Б. Т. Введение в оптимизацию / Б. Т. Поляк - М.: Наука, 1983 - 384 с. 10. Понтрягин Л.С. Математическая теория оптимальных процессов / Л.С. Понтрягин - М.: Наука, 1983. - 392 с. 11. Сухарев А.Г. Курс методов оптимизации / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров - М.: Наука, 2016. - 325 с. 12. Булавский В.А. Численные методы линейного программирования - М.: Наука, 2017. - 367с. 13. Болтянский В.Г. Математические методы оптимального управления - М.: Наука, 1969. - 408 с. 14. Васильев Ф.П. Линейное программирование / Ф.П. Васильев, А.Ю. Иваницкий - М.: «Факториал», 2018. - 176 с. 15. Гилл Ф. Практическая оптимизация / Ф. Гилл - М.: Мир, 1985. - 510с. 16. Грот О. Оптимальные статистические решения / О. Грот - М.: Мир, 2014. - 496с. 17. Демьянов В.Ф. Недифференцируемая оптимизация / В.Ф. Демьянов, Л.В. Васильев - М.: Наука, 2011. - 384 с. 18. Зельдович Я.Б. Элементы прикладной математики / Я.Б. Зельдович - М.: Наука, 2012. - 592с. 19. Кирин Н.Е. Методы последовательных оценок в задачах оптимизации управления системами / Н.Е. Кирин - Л: ЛГУ, 2010. - 160 с. 20. Кузнецов А.В. Математическое программирование / А.В. Кузнецов, В.А. Сакович, Н.И. Холод - Минск: Высшая школа. 1994. - 285 с. 21. Пшеничный Б.Н. Метод линеаризации / Б.Н. Пшеничный - М.: Наука, 1983. – 319 с. 22. Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах / Б.Н. Пшеничный, Ю.М. Данилин - М.: «Наука», 1975. - 320 с. 23. Прикладная математика и информатика: Курс лекций / Под ред. А. А. Колесникова. Л.: ВАС, 2017. - 209 с. 24. Реклейтис Г. Оптимизация в технике: В 2-х книгах. Пер. с англ. / Г. Реклейтис, А. Рейвиндран, К. Рэгсдел - М.: Мир, 1986. 25. Васильев Ф.П. Численные методы решения экстремальных задач / Ф.П. Васильев - М.: Наука, 2017. – 318 с. 26. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров - М.: Наука, 2016. – 275 с.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.4.244 (0.093 с.) |
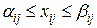 .
.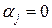 , а верхняя граница
, а верхняя граница 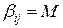 , где M - достаточно большое положительное число.
, где M - достаточно большое положительное число.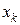 является дробное число. Тогда потребуется составить две новые задачи линейного программирования. Как это сделать?
является дробное число. Тогда потребуется составить две новые задачи линейного программирования. Как это сделать?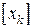 . В одной из новых задач линейного программирования нижней границей значения координаты
. В одной из новых задач линейного программирования нижней границей значения координаты 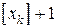 , то есть целая часть значения координаты, увеличенная на единицу. Это запишется следующим образом:
, то есть целая часть значения координаты, увеличенная на единицу. Это запишется следующим образом: 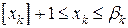 .
.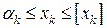 .
.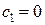 );
);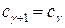 );
);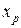 является целочисленным и максимальное значение целевой функции, найденное вместе с этим планом
является целочисленным и максимальное значение целевой функции, найденное вместе с этим планом 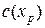 , больше ранее установленной нижней границы, то для следующей итерации устанавливается новая нижняя граница, то есть
, больше ранее установленной нижней границы, то для следующей итерации устанавливается новая нижняя граница, то есть 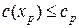 , то следует принять
, то следует принять 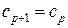 и выполнить шаг 1. В противном случае выполнять шаг 3.
и выполнить шаг 1. В противном случае выполнять шаг 3.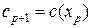 и выполнить шаг 1. В противном случае выполнить шаг 4.
и выполнить шаг 1. В противном случае выполнить шаг 4.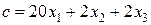 при системе ограничений
при системе ограничений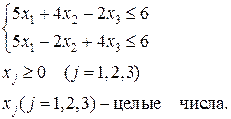
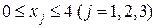
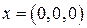 и нижнюю границу максимального значения целевой функции
и нижнюю границу максимального значения целевой функции 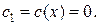
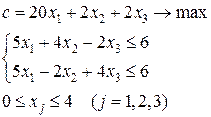
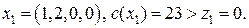
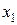 имеет дробную координату 1,2, то
имеет дробную координату 1,2, то 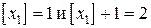 . Применяя границы значений неизвестных 1-й задачи, получаем новые задачи. Во 2-й задаче нижней границей для
. Применяя границы значений неизвестных 1-й задачи, получаем новые задачи. Во 2-й задаче нижней границей для 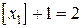 , а в 3-й задаче верхней границей для
, а в 3-й задаче верхней границей для 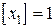 .
.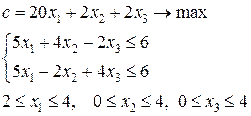
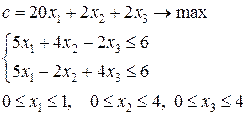
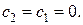
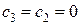 и следует следующая итерация.
и следует следующая итерация.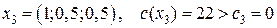
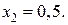 Тогда
Тогда 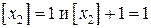 . Применяя границы значений неизвестных из 3-й задачи, получаем две новых задачи.
. Применяя границы значений неизвестных из 3-й задачи, получаем две новых задачи.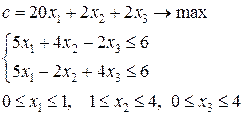
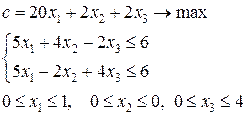
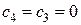 .
.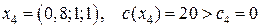
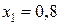 и получаем
и получаем 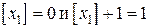 . Применяя границы значений переменной
. Применяя границы значений переменной 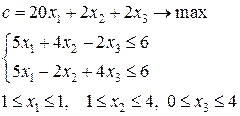
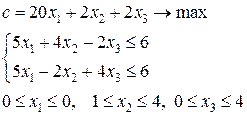
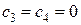 .
.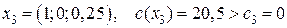
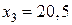 и получаем
и получаем 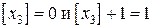 . Применяя границы значений неизвестной
. Применяя границы значений неизвестной 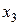 5-й задачи, получаем две новые задачи.
5-й задачи, получаем две новые задачи.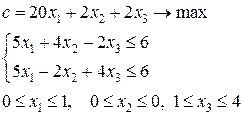
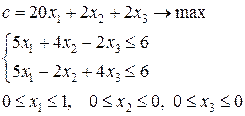
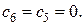
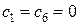 и следует следующая итерация.
и следует следующая итерация.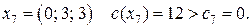
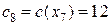 и далее следует итерация 8.
и далее следует итерация 8.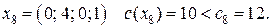
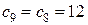 , далее - следующая итерация.
, далее - следующая итерация.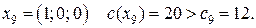
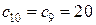 и переходим к следующей итерации.
и переходим к следующей итерации.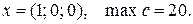
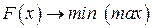 (31)
(31)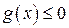 , (32)
, (32)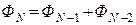 при
при 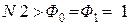 .
.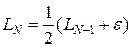
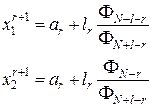
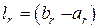 – длина интервала неопределенности на r -ом шаге;
– длина интервала неопределенности на r -ом шаге;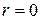 ) симметрично от концов начального интервала неопределенности (а и b) проводится пара испытаний в точках
) симметрично от концов начального интервала неопределенности (а и b) проводится пара испытаний в точках 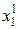 и
и 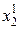 , определяемых N -ом и (N –1) числами Фибоначчи. Получаем
, определяемых N -ом и (N –1) числами Фибоначчи. Получаем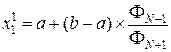
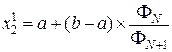
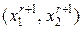 .
.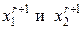 , рассматриваемых на (r +1)-м шаге, одна всегда будет совпадать с одной из точек предыдущего шага
, рассматриваемых на (r +1)-м шаге, одна всегда будет совпадать с одной из точек предыдущего шага 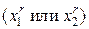 , в которой уже было проведено испытание.
, в которой уже было проведено испытание.