
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая задача линейного программирования
Дана система m линейных уравнений и неравенств с n переменными
………………………….
…………………………..,
где и линейная функция
где необходимо найти такое решение системы
при котором линейная функция f (1) принимает оптимальное значение. Система (1) называется системой ограничений, а функция f – линейной функцией. Оптимальным решением задачи линейного программирования называется решение 4.1. Основные определения Любые m переменных системы m линейных уравнений с n переменными Теорема 1. если для системы m линейных уравнений с n переменными Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все Угловая точка – точка множества, которая не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству. Теорема 2. если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более, чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой комбинацией этих точек. Оптимум линейной функции задачи линейного программирования следует искать среди конечного числа ее допустимых базисных решений. Пример решения задачи линейного программирования Задача 1. (об использовании ресурсов). Для изготовления двух видов продукции р1 и р2 используют четыре вида ресурсов s1, s2, s3, s4. запасы ресурсов, затрачиваемых на производство единицы продукции, приведены в таблице 1.
Таблица 1
Прибыль, получаемая от единицы продукции р1 и р2 – соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Геометрический метод решения. Составим экономико-математическую модель задачи. Обозначим
по смыслу задачи переменные х1³0, х2³0 (5) суммарная прибыль f составит
итак, экономико-математическая модель задачи: найти такой план выпуска продукции
при ограничениях:
Изобразим многоугольник решений на рис. 1
Рис. 1. Очевидно, что при
откуда Максимум (максимальное значение) линейной функции равен Итак,
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.204 (0.012 с.) |
|||||||||||||||||||||||||||||
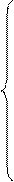
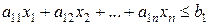 ,
,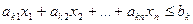 , (1)
, (1)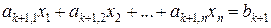 ,
,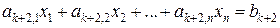 ,
,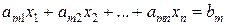

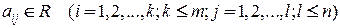 .
.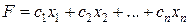 , (2)
, (2)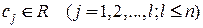 .
.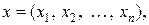 где
где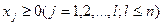 (3)
(3)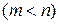 называются основными или базисными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные
называются основными или базисными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные 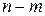 переменных называются неосновными.
переменных называются неосновными.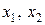 - число единиц продукции соответственно
- число единиц продукции соответственно 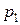 и
и 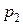 , запланированных к производству. Для их изготовления потребуется
, запланированных к производству. Для их изготовления потребуется 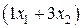 единиц ресурса
единиц ресурса 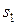 ,
, 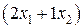 единиц ресурса s2,
единиц ресурса s2, 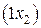 единиц ресурса
единиц ресурса 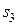 и
и 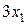 единиц ресурса
единиц ресурса 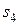 . Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
. Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств: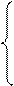
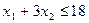 ,
,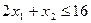 , (4)
, (4)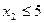 ,
,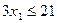 .
.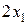 руб. от реализации продукции
руб. от реализации продукции 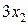 руб. - от реализации продукции р2, т.е.
руб. - от реализации продукции р2, т.е.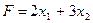 (6)
(6)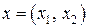 , удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение:
, удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение: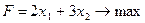
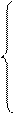
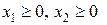 (v,vi)
(v,vi) 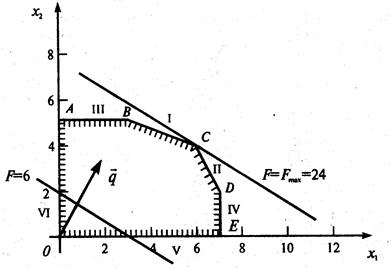
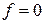 линия уровня
линия уровня 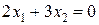 проходит через начало координат (строить ее не обязательно). Зададим, например,
проходит через начало координат (строить ее не обязательно). Зададим, например, 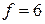 и построим линию уровня
и построим линию уровня 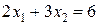 . Ее расположение указывает на направление возрастания линейной функции (вектор
. Ее расположение указывает на направление возрастания линейной функции (вектор 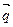 ). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений
). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений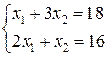
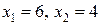 , т.е. С (6;4).
, т.е. С (6;4).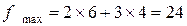 .
.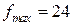 при оптимальном решении
при оптимальном решении 


