
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра автоматизации производственных процессовСтр 1 из 10Следующая ⇒
Кафедра автоматизации производственных процессов Лапшина М.Л. Учебное пособие по дисциплине МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ
Воронеж 2019 Содержание
ВВЕДЕНИЕ Методы решения задач оптимизации являются одним из разделов исследования операций – научной дисциплины, занимающейся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами. Управление любой системой реализуется как процесс, подчиняющийся определенным закономерностям, их знание помогает определить условия, необходимые и достаточные для осуществления данного процесса. для этого все параметры, характеризующие процесс и внешние условия, должны быть количественно определены, измерены. В данном разделе выделяется большой класс оптимизационных моделей, такие задачи возникают при попытке оптимизировать планирование и управление сложными экономическими системами.
при решении конкретной задачи управления применение методов исследования операций предполагает: · построение экономических и математических моделей для задач принятия решений в сложных ситуациях или в условии неопределенности; · изучение взаимосвязей, определяющих в последствие принятие решений, и установление критериев эффективности, позволяющих оценить преимущество того или иного варианта действия. ОПТИМИЗАЦИОННАЯ МОДЕЛЬ Оптимальная (или оптимизационная) модель [optimization model] - экономико-математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них. В отличие от дескриптивной (описательной, балансовой) модели о. м. содержит наряду с уравнениями, описывающими взаимосвязи между переменными, также критерий для выбора – функционал (или, что то же, целевую функцию). О. м. - основной инструмент экономико-математических методов. обычно они очень сложны, насчитывают сотни и тысячи уравнений и переменных. но общая структура таких моделей проста. она состоит из целевой функции, способной принимать значения (на множестве значений переменных) в пределах области, ограниченной условиями задачи (области допустимых решений), и ограничений, характеризующих эти условия. целевая функция в самом общем виде в свою очередь состоит из трех элементов: управляемых переменных, параметров (или также переменных), которые не поддаются управлению (напр., зависящих от внешней среды), и формы зависимости между ними (формы функции). Для того чтобы использовать результаты и вычислительные процедуры теории оптимизации на практике, необходимо прежде всего построить математическую модель объекта оптимизации. Под математической моделью любой реальной системы принято понимать совокупность соотношений, определяющих характеристики состояний системы в зависимости от начальных условий и времени
В практике исследования объектов модели могут применяться для самых разных целей, что вызывает использование моделей различных классов. Построение одной модели для сложной системы практически не представляется возможным без разработки вспомогательных моделей. поэтому при создании конечной математической модели исследуемого объекта строят частные вспомогательные модели, отражающие ту или иную информацию об объекте, имеющуюся у разработчика на данном этапе построения модели. для построения модели необходима система правил (принципов), позволяющих корректно осуществлять процесс построения. Общие принципы системного экономико-математического моделирования вытекают из общих принципов системного анализа: 1. принцип достаточности используемой информации; 2. принцип инвариантности используемой информации; 3. принцип преемственности модели; 4. принцип эффективной реализуемости комплекса экономико-математических моделей. При рассмотрении экономико-математических моделей оперируют следующими понятиями: критерий оптимальности, целевая функция, система ограничений, уравнения связи, решение модели. Критерием оптимальности называется некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции через факторы модели. Критерий оптимальности определяет смысловое содержание целевой функции. Целевая функция математически связывает между собой факторы модели, и ее значение определяется значениями этих величин. Содержательный смысл целевой функции придает только критерий оптимальности. при наличии нескольких критериев оптимальности каждый из них будет описываться своей частной целевой функцией. система ограничений определяет пределы, сужающие область осуществимых или допустимых решений и фиксирующие основные внешние и внутренние свойства объекта. ограничения определяют область протекания процесса, пределы изменения параметров и характеристик объекта. Уравнения связи являются математической формализацией системы ограничений. Различные по смыслу ограничения могут описываться одинаковыми уравнениями связи, а одно и то же ограничение в разных моделях может описываться разными уравнениями связи. Решением математической модели называется такой набор (совокупность) значений переменных, который удовлетворяет ее уравнениям связи. Общих способов построения математических моделей не существует, но можно условно разбить процесс на следующие основные этапы: 1. определение границ объекта оптимизации; 2. выбор управляемых переменных; 3. определение ограничений на управляемые переменные; 4. выбор критерия оптимизации; 5. формулировка математической задачи Оптимальная (или оптимизационная) задача [optimization problem] - экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличных ресурсов, иногда то же, экстремальная задача решается с помощью оптимальной модели методами математического программирования, т. е. путем поиска максимума или минимума некоторых функций или функционалов при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация).
Решение о. з. называется оптимальным решением, оптимальным планом, оптимальной точкой.
Пример решения задачи линейного программирования Задача 1. (об использовании ресурсов). Для изготовления двух видов продукции р1 и р2 используют четыре вида ресурсов s1, s2, s3, s4. запасы ресурсов, затрачиваемых на производство единицы продукции, приведены в таблице 1. Таблица 1
Прибыль, получаемая от единицы продукции р1 и р2 – соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Геометрический метод решения. Составим экономико-математическую модель задачи. Обозначим
по смыслу задачи переменные х1³0, х2³0 (5) суммарная прибыль f составит
итак, экономико-математическая модель задачи: найти такой план выпуска продукции
при ограничениях:
Изобразим многоугольник решений на рис. 1
Рис. 1. Очевидно, что при
откуда Максимум (максимальное значение) линейной функции равен Итак,
Пример решения задачи симплексным методом Задача 1 (п.4.2). Решение. С помощью дополнительных неотрицательных переменных перейдем к системе уравнений. В данном случае все дополнительные переменные вводятся со знаком “плюс”, так как все неравенства имеют вид «≤».
Для нахождения первоначального базисного решения разобьем переменные на две группы - основные и неосновные. так как определитель, составленный из коэффициентов при дополнительных переменных х3, х4, х5,х6, отличен от нуля, то эти переменные можно взять в качестве основных на первом шаге решения задачи. При выборе основных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и проверять, равен ли он нулю. Достаточно воспользоваться следующим правилом: в качестве основных переменных на первом шаге следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не ходит ни одна из этих переменных. Дополнительные переменные удовлетворяют этому правилу. Если выбранные по этому правилу переменные имеют те же знаки, что и соответствующие им свободные члены в правых частях уравнений, то полученное таким образом базисное решение будет допустимым. В данном случае так и получилось. i шаг. Основные переменные: х3, х4, х5, х6. неосновные переменные: х1, х2. Выразим основные переменные через неосновные:
Положив неосновные переменные равными нулю, т.е. х1 =0, х2 = 0, получим базисное решение х1= (0; 0; 18; 16; 5; 21), которое является допустимым и соответствует вершине О (0;0) многогранника ОАВСDЕ на рис. 2.
Рис. 2 Поскольку это решение допустимое, нельзя отбросить возможность того, что оно оптимально. выразим линейную функцию через неосновные переменные: При решении х1 значение функции равно
Система (1) накладывает ограничения на рост переменной х2. поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом х1 = 0 как неосновная переменная):
Каждое уравнение системы (1), кроме последнего, определяет оценочное отношение - границу роста переменной х2, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при х2 при условии, что эти числа имеют разные знаки. Последнее уравнение системы не ограничивает рост переменной х2, так как данная переменная в него не входит (или формально входит с нулевым коэффициентом). В этом случае условимся обозначать границу символом ∞. Такой же символ будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как и в этом случае нет ограничений на рост переменной. Не накладывает ограничений на рост переменной, переводимой в основные, и такое уравнение, где свободный член отсутствует (т.е. равен 0), а переводимая переменная имеет положительный коэффициент. И в этом случае граница обозначается символом ∞. Обратите внимание, что при нулевом свободном члене и отрицательном коэффициенте при переводимой переменной уравнение ограничивает рост этой переменной нулем! (любое положительное ее значение вносит отрицательную компоненту в следующее базисное решение). Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. В данном примере наибольшее возможное значение для переменной х2 определяется как х2 =min (18/3; 16/1; 5/1; ∞} =5. при х2 =5 переменная х5 обращается в нуль и переходит в неосновные. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минимальна), называется разрешающим. В данном случае - это третье уравнение. разрешающее уравнение будем выделять рамкой в системе ограничений. ii шаг. Основные переменные: х2, х3,х4, х6. неосновные переменные: х1, х5. Выразим новые основные переменные через новые неосновные, начиная с разрешающего уравнения (его используем при записи выражения для х2):
или
Второе базисное решение Выразив линейную функцию через неосновные переменные на этом шаге, получаем:
Значение линейной функции f2 = f (х2) =15. изменение значения линейной функции легко определить заранее как произведение наибольшего возможного значения переменной, переводимой в основные, на ее коэффициент в выражении для линейной функции; в данном случае Однако значение f2 не является максимальным, так как повторяя рассуждения 1 шага, обнаруживаем возможность дальнейшего увеличения линейной функции за счет переменной х1, входящей в выражение для f с положительным коэффициентом. Система уравнений (8) определяет наибольшее возможное значение для х1: х1 = min{∞;3/1;11/2; ∞} = 3. второе уравнение является разрешающим, переменная х3 переходит в неосновные, при этом iii шаг. Основные переменные: х1, х2, х4, х6. неосновные переменные х3, х5. Как и на ii шаге, выражаем новые основные переменные через новые неосновные, начиная с разрешающего уравнения (его используем при записи выражения для хi). после преобразований получаем:
Базисное решение х3 = (3; 5; 0; 5; 0; 12) соответствует вершине в (3;5). выражаем линейную функцию через неосновные переменные iv шаг. Основные переменные: х1, х2, х5, х6. неосновные переменные: х3, х4. После преобразований получим:
Базисное решение Линейная функция, выраженная через неосновные переменные, имеет вид: Прибыль предприятия принимает максимальное значение 24 руб. при реализации 6 единиц продукции Метод искусственного базиса Суть метода: в каждое уравнение, дающее отрицательную компоненту в базисном решении, вводим свою новую неотрицательную искусственную переменную у1,у2,…, уk, которая имеет тот же знак, что и свободный член в правой части уравнения. В первой таблице включаем в число основных все искусственные переменные и те обычные добавочные переменные, которые определяют неотрицательные компоненты базисного решения. Составляем новую линейную функцию 1. Если в оптимальном решении т-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. 2. Если имеется оптимальное решение т-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна. 3. Если Тmax= ∞, то исходная задача также неразрешима, причем либо fmax=∞, либо условия задачи противоречивы. Из теоремы следует, что вначале следует найти минимум м- функции. если он равен 0 и все искусственные переменные обращаются в 0, то далее можно отбросить эти переменные и решать исходную задачу, исходя из полученного допустимого базисного решения. на практике находят не минимум м-функции, а максимум (-м)-функции. Пример двойственной задачи Составить задачу, двойственную следующей задаче:
при ограничениях:
Решение. Так как исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду «≤», для чего обе части первого и четвертого неравенства умножим на (-1), получим:
2. Составим расширенную матрицу системы:
4. Сформулируем двойственную задачу:
ТРАНСПОРТНАЯ ЗАДАЧА Особенности экономико-математической модели транспортной задачи: • система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме); • коэффициенты при переменных системы ограничений равны единице или нулю; • каждая переменная входит в систему ограничений два раза. Для математической формулировки транспортной задачи в общей постановке обозначим через c ij коэффициенты затрат, через мi - мощности поставщиков, через nj - мощности потребителей, где
Система (16) включает в себя уравнение баланса по строкам, а система (17) - по столбцам таблицы поставок. Линейная функция в данном случае
Математическая формулировка транспортной задачи в общей постановке будет следующей: на множестве неотрицательных (допустимых) решений системы ограничений (16), (17) найти такое решение Произвольное допустимое решение Транспортная задача, приведенная в примере (см. ниже), обладает важной особенностью: суммарная мощность поставщиков равна суммарной мощности потребителей, т.е.
Такие транспортные задачи называются закрытыми (говорят также, что транспортная задача в этом случае имеет закрытую модель). В противном случае транспортная задача называется открытой (открытая модель транспортной задачи). Рассмотрим закрытую транспортную задачу, являясь задачей линейного программирования, транспортная задача может быть решена симплексным методом. Однако, специфичная форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом. По аналогии с общим случаем решение в нем осуществляется по шагам, и каждому шагу соответствует разбиение переменных на основные (базисные) и неосновные (свободные). Число r основных переменных транспортной задачи равно рангу системы линейных уравнений (максимальному числу линейно независимых уравнений в системе ограничений).
Пример транспортной задачи Построить экономико-математическую модель следующей задачи. имеются три поставщика и четыре потребителя. мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары “поставщик - потребитель” сведены в таблицу поставок (табл. 3). Таблица 3
В левом верхнем углу произвольной (ij -клетки (i - номер строки, j - номер столбца) стоит так называемый коэффициент затрат - затраты на перевозку единицы груза от i-го поставщика к j -му потребителю, например, в левом верхнем углу клетки (1, 4) стоит число 3, следовательно, перевозка единицы груза от 1-го поставщика к 4-му потребителю обойдется в 3 условных денежных единицы и т. д. Задача ставится следующим образом: найти объемы перевозок для каждой пары «поставщик — потребитель» так, чтобы: 1) мощности всех поставщиков были реализованы; 2) спросы всех потребителей были удовлетворены; 3) суммарные затраты на перевозку были бы минимальны. Решение. Построим экономико-математическую модель данной задачи, искомый объем перевозки от i-го поставщика к j -му потребителю обозначим черёз xij и назовём поставкой клетки (i,j). Например, х12 - искомый объем перевозки от 1- го поставщика ко 2-му потребителю или поставка клетки (1,2) и т. д. заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных х. так, например, объем груза, забираемого от 1 -го поставщика, должен быть равен мощности этого поставщика - 60 единицам, т.е.
Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляем для каждого столбика таблицы поставок:
Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что
Суммарные затраты р на перевозку выражаются через коэффициенты затрат и поставки следующим образом;
Найдем первоначальное базисное распределение поставок для транспортной задачи методом «северо-западного угла». Решение. дадим переменной х11 максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) - “северо-западный” угол таблицы поставок: х11= min {60, 20) = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадет из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией (табл. 4) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. в таблице поставок найдем новый “северо-западный” угол - клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60 - 20 единиц груза, получаем, что Таблица 4.
Решение методом наименьших затрат. Решение. Находим в таблице поставок (табл.4) клетки с наименьшим коэффициентом затрат. Таких клеток две – (1,1) и (2,1) с коэффициентами затрат, равными 1. сравним максимально возможные поставки для этих клеток: для клетки (1,1)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.155 (0.143 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

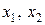 - число единиц продукции соответственно
- число единиц продукции соответственно 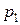 и
и 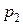 , запланированных к производству. Для их изготовления потребуется
, запланированных к производству. Для их изготовления потребуется 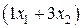 единиц ресурса
единиц ресурса 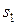 ,
, 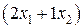 единиц ресурса s2,
единиц ресурса s2, 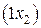 единиц ресурса
единиц ресурса 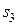 и
и 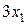 единиц ресурса
единиц ресурса 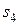 . Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
. Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств: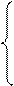
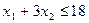 ,
,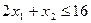 , (4)
, (4)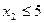 ,
,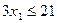 .
.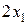 руб. от реализации продукции
руб. от реализации продукции 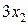 руб. - от реализации продукции р2, т.е.
руб. - от реализации продукции р2, т.е.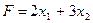 (6)
(6)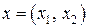 , удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение:
, удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение: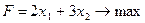
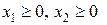 (v,vi)
(v,vi) 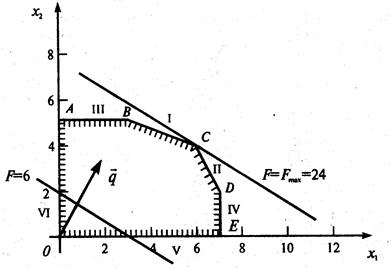
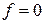 линия уровня
линия уровня 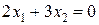 проходит через начало координат (строить ее не обязательно). Зададим, например,
проходит через начало координат (строить ее не обязательно). Зададим, например, 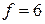 и построим линию уровня
и построим линию уровня 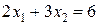 . Ее расположение указывает на направление возрастания линейной функции (вектор
. Ее расположение указывает на направление возрастания линейной функции (вектор 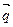 ). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений
). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений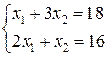
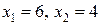 , т.е. С (6;4).
, т.е. С (6;4).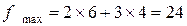 .
.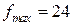 при оптимальном решении
при оптимальном решении 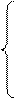 Получим систему ограничений в виде:
Получим систему ограничений в виде: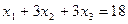 ,
,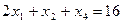 ,
,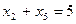 ,
,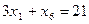 .
.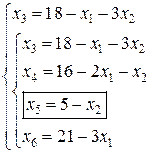 , (7)
, (7)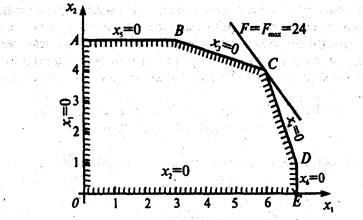
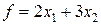 .
.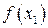 . Легко понять, что функцию f можно увеличить за счет увеличения любой из неосновных переменных, входящих в выражение для f с положительным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная будет неосновной, т.е. принимать не нулевое, а положительное значение (если новое решение будет вырождено, то функция цели сохранит свое значение). При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многоугольника, где значение линейной функций “лучше” (по крайней мере “не хуже”). В данном примере для увеличения f можно переводить в основные либо х1, либо х2, так как обе эти переменные входят в выражение дня f со знаком “плюс”. Для определенности в такой ситуации будем выбирать переменную, имеющую больший коэффициент, т.е. в данном случае х2 (такое правило выбора не всегда дает наименее трудоемкое решение, иногда имеет смысл провести предварительные специальные оценки).
. Легко понять, что функцию f можно увеличить за счет увеличения любой из неосновных переменных, входящих в выражение для f с положительным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная будет неосновной, т.е. принимать не нулевое, а положительное значение (если новое решение будет вырождено, то функция цели сохранит свое значение). При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многоугольника, где значение линейной функций “лучше” (по крайней мере “не хуже”). В данном примере для увеличения f можно переводить в основные либо х1, либо х2, так как обе эти переменные входят в выражение дня f со знаком “плюс”. Для определенности в такой ситуации будем выбирать переменную, имеющую больший коэффициент, т.е. в данном случае х2 (такое правило выбора не всегда дает наименее трудоемкое решение, иногда имеет смысл провести предварительные специальные оценки).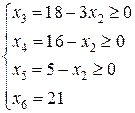 откуда
откуда 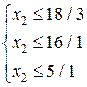
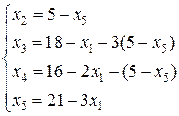
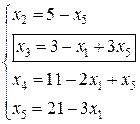 (8)
(8)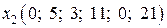 является допустимым и соответствует вершине а (0;5) на рис. 2. Геометрическая интерпретация перехода от х1 к х2 — переход от вершины о к соседней вершине а на многоугольнике решений ОАBCDЕ.
является допустимым и соответствует вершине а (0;5) на рис. 2. Геометрическая интерпретация перехода от х1 к х2 — переход от вершины о к соседней вершине а на многоугольнике решений ОАBCDЕ.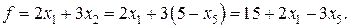
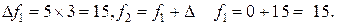
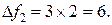
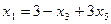 ,
,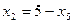 ,
,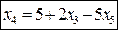 , (9)
, (9)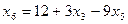 .
.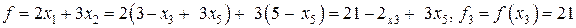 . Проверяем:
. Проверяем: 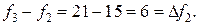 Третье допустимое базисное решение тоже не является оптимальным, поскольку при неосновной переменной х5 в выражении линейной функции через неосновные переменные содержится положительный коэффициент. Переводим х5 в основную переменную. при определении наибольшего возможного значения для х5 следует обратить внимание на первое уравнение в системе (9), которое не дает ограничений на рост х5, так как свободный член и коэффициент при х5 имеют одинаковые знаки. Поэтому
Третье допустимое базисное решение тоже не является оптимальным, поскольку при неосновной переменной х5 в выражении линейной функции через неосновные переменные содержится положительный коэффициент. Переводим х5 в основную переменную. при определении наибольшего возможного значения для х5 следует обратить внимание на первое уравнение в системе (9), которое не дает ограничений на рост х5, так как свободный член и коэффициент при х5 имеют одинаковые знаки. Поэтому 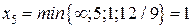 . Третье уравнение является разрешающим, и переменная х4 переходит в неосновные;
. Третье уравнение является разрешающим, и переменная х4 переходит в неосновные; 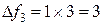 .
.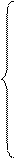
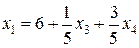 ,
,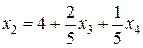 ,
,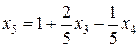 ,
,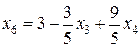 .
.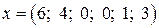 соответствует вершине с (6; 4) на рис. 2.
соответствует вершине с (6; 4) на рис. 2.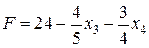 .это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому значение
.это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому значение 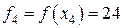 максимальное. Функцию f невозможно еще увеличить, переходя к другому допустимому базисному решению, т.е. решение х4 оптимальное. Вспоминая экономический смысл всех переменных, можно сделать следующие выводы.
максимальное. Функцию f невозможно еще увеличить, переходя к другому допустимому базисному решению, т.е. решение х4 оптимальное. Вспоминая экономический смысл всех переменных, можно сделать следующие выводы.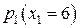 и 4 единиц продукции
и 4 единиц продукции 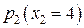 Дополнительные переменные х3, х4, х5, х6 показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптимальном плане производства
Дополнительные переменные х3, х4, х5, х6 показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптимальном плане производства 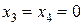 , т.е. остатки ресурсов s1 и s2 равны нулю, а остатки, ресурсов s3 и s4 равны соответственно 1 и 3 единицам.
, т.е. остатки ресурсов s1 и s2 равны нулю, а остатки, ресурсов s3 и s4 равны соответственно 1 и 3 единицам.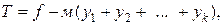 где м - произвольно большое число, и ищем ее максимум (т-задача). Назовём м-функцией выражение
где м - произвольно большое число, и ищем ее максимум (т-задача). Назовём м-функцией выражение 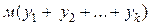 . Справедлива теорема:
. Справедлива теорема: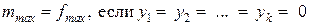 т.е. минимум м-функции равен 0).
т.е. минимум м-функции равен 0).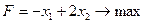
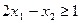 ,
,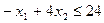 ,
,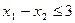 ,
,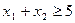 ,
,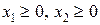
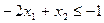 ,
,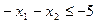

 а1=
а1= 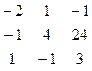
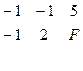
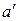 транспонированную к а1:
транспонированную к а1:
 а1¢=
а1¢= 
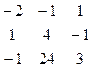
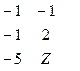
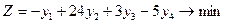
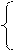 при ограничениях
при ограничениях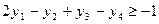
 ,
,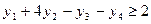 ,
,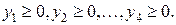
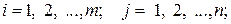 m - число поставщиков, n - число потребителей. Тогда система ограничений примет вид:
m - число поставщиков, n - число потребителей. Тогда система ограничений примет вид: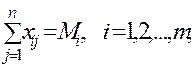 (16)
(16)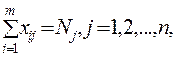 (17)
(17)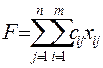 . (18)
. (18)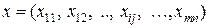 , при котором значение линейной функции (18) минимально.
, при котором значение линейной функции (18) минимально.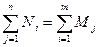
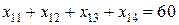 (уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т. е.
(уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т. е.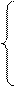
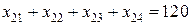 , (19)
, (19)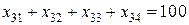 .
. 
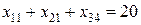 ,
,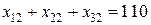 , (20)
, (20)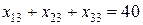 ,
,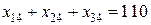 .
. 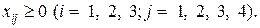
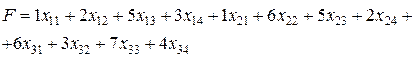 (21)
(21)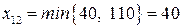 . После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). в оставшейся таблице снова находим “северо-западный угол” и т. д. в результате получаем следующее исходное распределение поставок (табл.4).
. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). в оставшейся таблице снова находим “северо-западный угол” и т. д. в результате получаем следующее исходное распределение поставок (табл.4).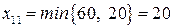 , для клетки (2,1)
, для клетки (2,1) 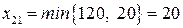 .
.


