
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет надежности с применением математической логики иСодержание книги
Поиск на нашем сайте
структурных преобразований К основным методам расчета надежности с применением математической логики относятся: метод перебора гипотез, логико-вероятностный метод и метод структурного преобразования схем [4].
Метод перебора гипотез. Для применения данного метода необходимо сделать следующие допущения о невосстанавливаемой системе: 1. Система состоит из n элементов и имеет любую структуру; 2. У каждого элемента есть два состояния: рабочее и состояние отказа; 3. Принимается, что вероятность рабочего состояния - рi, а отказного - qi, то есть рi + qi = 1. Принимая во внимание перечисленные допущения, составляются следующие гипотезы: · H0 - все элементы работоспособны; · Hi - i -й элемент отказал, остальные элементы работоспособны; · Hi,j - i -й и j -й элементы отказали, остальные работоспособны; · H1,2,….,n - все элементы отказали. Предполагая отказы элементов независимыми событиями, вероятность каждой гипотезы определяется следующими выражениями
…
Для определения вероятности, при которой система будет работать без отказов, необходимо произвести суммирование вероятностей гипотез, соответствующих рабочим состояниям системы. Из-за того, что система имеет очень большое количество состояний, данный способ на практике применяется очень редко – перебор гипотез является трудоемким и занимает достаточно большое количество времени [2]. Логико-вероятностный метод. Постановка задачи и суть логико-вероятностного метода оценки надежности заключается в описании схемы системы с помощью средств математической логики. После этого, при определении показателей надежности, используются теоремы теории вероятности. В основе расчетов, которые проделываются при данном методе оценки надежности системы, лежат операции с событиями и высказываниями на базе булевой алгебры (алгебры высказываний). Объектом исследований булевой алгебры являются высказывания. Зная высказывание, либо задавшись им, можно утверждать о его истинности или ложности. В свою очередь высказывания могут быть простыми и сложными. Сложное высказывание - это высказывание, состоящее из простых, которые соединяются между собой логическими операциями. Каждая из логических операций устанавливает логическую связь между истинностью ложного высказывания и истинностью простых высказываний. Принято, что истинность высказываний обозначается единицей, а ложность - нулем [2]. Метод структурного преобразования схем. Суть метода структурного преобразования схем (эквивалентного преобразования схем) состоит в том, что изначальную схему необходимо переделать, представив в виде участков. Элементы схемы на каждом из участков могут соединяться или последовательно, или параллельно. Затем необходимо произвести упрощение схемы. Упрощать исходную схему необходимо так, чтобы новая схемы была подобна исходной. Упрощение производится соединением или разъединением узлов схемы. Исполнитель сам в праве выбирать какой узел куда переставить. В итоге имеем эквивалентную схему. Если на изначальную и эквивалентную схемы подать одинаковое напряжение, то ток в обеих цепях потечет одинаковый. Преимущество метода структурного преобразования схем заключается в том, что все расчеты необходимо производить с эквивалентной схемой, что значительно упрощает процесс и затраты по времени [2]. Для того, чтоб описать условия работоспособности объекта также в математической логике используются: · Дизъюнкция – замена ИЛИ
· Конъюнкция - И
· Отрицание
Порядок использования математической логики для определения надежности: · Словесно сформулировать условия работоспособности объекта; · Записать логическую функцию; · Минимизировать(упростить) функцию; · Перейти от логической функции к арифметической; · Заменить события вероятностями их появления; · Вместо обозначений вероятности перейти к числовым значениям.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.006 с.) |

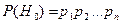 ,
,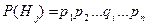 ,
,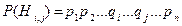
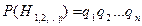 .
.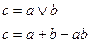 ;
;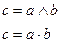 ;
;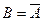 .
.


