
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения отказовСодержание книги
Поиск на нашем сайте
1. Среднее значение случайной величины Случайная величина х, функция распределения F(x), плотность распределения Тогда:
2. Дисперсия – мера отклонения случайной величины от ее математического ожидания.
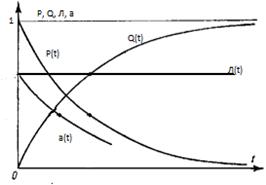
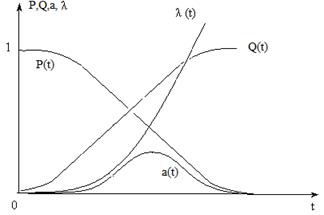
3. Среднеквадратическое отклонение (СКО) – отклонение некоторой величины от какого-то заданного значения. СКО определяется формулой · Экспоненциальный закон – применяется для периода нормальной эксплуатации любого технического устройства. Чаще всего применяется для электронных систем. Часто используется для пускорегулировочной аппаратуры.
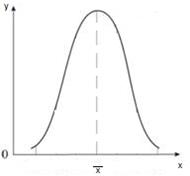
Рисунок 2.2 – Экспоненциальный закон · Нормальный закон – характерен для периода износа любого технического устройства. Нормальному закону подчиняются отказы объектов, на которые оказывает влияние ряд случайных величин, каждая из которых не имеет доминирующего характера. Эти случайные величины группируются около некоторого среднего значения (с определенными частотами), которые называется математическим ожиданием. Такому закону подчиняются отказы щеток и контактных колец.
Рисунок 2.3 – Нормальный закон Чтобы упростить расчет, вводится функция Лапласа:
Рисунок 2.4 – Нормальный закон с учетом функции Лапласа
· Распределение Вейбулла Для механических и электромеханических узлов является двухпараметрическим распределением: k – параметр асимметрии,
Если k =1, тогда имеем экспоненциальный закон. Если k >1, тогда приближаемся к нормальному закону. Если k <1, тогда все основные показатели надежности монотонно уменьшаются.
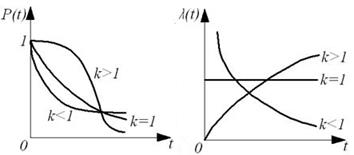
Рисунок 2.5 – Распределение Вейбулла · Гамма-распределение – применяется для сложных резервированных систем. Является двухпараметрическим: k – параметр асимметрии,
Рисунок 2.6 – Гамма-распределение · Биномиальное распределение – характерно для событий, имеющих 2 исхода, взаимно исключающих друг друга. Имеется большая совокупность объектов, где р - исправные, q – неисправные. Из этой совокупности берется выборка объема n:
· Распределение Пуассона – характерно для контроля качества объектов; представляет собой ряд, сумма членов которого равняется 1. Каждый из членов представляет собой вероятность появления 0, 1, 2, 3 или большего числа неисправностей, приходящихся на 1 объект.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.006 с.) |

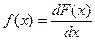 .
. 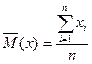 ,
, 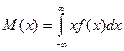 .
.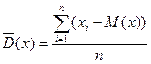 ,
, 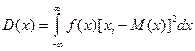 .
.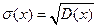 .
.
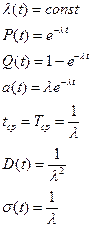
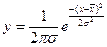
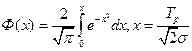 .
.
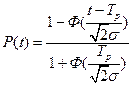
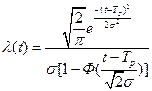
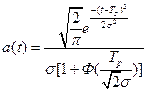
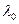 - параметр масштаба.
- параметр масштаба.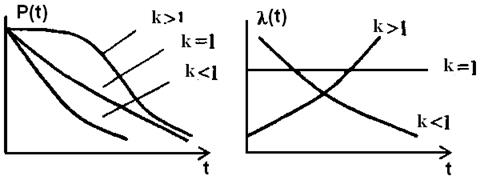
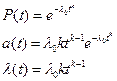
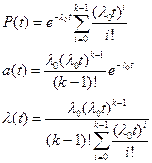
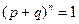 . Тогда вероятность появления различного числа исправных (неисправных) объектов в выборке объема n определяется коэффициентами членов биномиального распределения
. Тогда вероятность появления различного числа исправных (неисправных) объектов в выборке объема n определяется коэффициентами членов биномиального распределения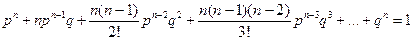 .
.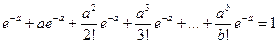 .
.


