
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические аспекты линейной алгебрыСтр 1 из 5Следующая ⇒
Элементы линейной алгебры
Разработчик: Есенеева Э.С. ВВЕДЕНИЕ Современная математика характеризуется интенсивным проникновением в другие науки, во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики оказался универсальным, и это есть объективное отражение универсальности законов окружающего нас многообразного мира. Для будущего специалиста любой отрасли изучение математических дисциплин и их экономических приложений, составляющих основу актуальной экономической математики, позволит не только приобрести необходимые базовые навыки, используемые в экономике, но и сформировать компоненты своего мышления: уровень, кругозор и культуру. Одним из основных разделов математики, где широко используются экономические методы решения задач, является раздел «Линейная алгебра». Особенно этот вопрос стал актуальным при разработке и использовании баз данных, так как при работе с ними почти вся информация хранится и обрабатывается в матричной форме. С помощью матриц удобно описывать различные экономические закономерности. Кроме этого около 75% всех расчетных математических задач приходится на решение систем линейных алгебраических уравнений (СЛАУ). Это задачи из области экономики, статистики, электротехники, радиоэлектроники, механики и других. Таким образом, элементы линейной алгебры позволяют описывать те или иные процессы, происходящие в различных сферах деятельности человека. Изучение данного раздела, умение составлять модели процессов с использованием систем линейных уравнений и матриц дает возможность использования полученных знаний в решении конкретных проблем, возникающих в будущей практической профессиональной деятельности. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Понятие матрицы Впервые матрица под названием "волшебный квадрат" упоминается еще в Древнем Китае. Подобные квадраты чуть позже были известны и у арабских математиков. Матрица (размером m x n) - это таблица чисел, содержащая m строк и n столбцов. При этом сами числа называются элементами матрицы, и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
Для обозначения матрицы используются прописные латинские буквы (A, B, C,..), а саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицыобозначают строчными латинскими буквами, снабженными двумя индексами. Например: aij - элемент матрицы А, расположенный в i-й строке и j-м столбце или коротко элемент в позиции ( i,j ). В общем виде матрица размера m на n может быть записана следующим образом
Некоторые экономические зависимости удобно записывать в виде матриц. В пример приведем таблицу распределения ресурсов по отдельным отраслям экономики (в ус. ед). Пример 1:
Эти данные в таблице можно представить в удобной форме в виде матрицы распределение ресурсов по отраслям:
В данном примере, матричный элемент а11 показывает, какое количество электроэнергии потребляет промышленность, а элемент а22 - количество трудовых ресурсов в сельском хозяйстве.
матрица А размером 2 х 4.
матрица B размером 4 x 2.
Элементы aij, где i=j, называются диагональными, а элементы aij, где i≠j - внедиагональными. Определение: Матрица, все элементы которой равны нулю, называется нулевой матрицей. Пример 3:
Определение: Матрица, у которой число строк равно числу столбцов (m=n) называется квадратной матрицей порядка n. Пример 4:
квадратная матрица С порядка 3.
Определение: Матрица размера 1 x n называется матрицей-строкой или вектор-строкой. Матрица размера m x 1 называется матрицей столбцом или вектор-столбцом. Пример 5:
Определение: Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.
Пример 6:
1.2.1 Действия над матрицами. 1. Сложение: Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц
Пример 1:
Аналогично определяется разность матриц. 2.Умножение на число: Произведением матрицы Пример 2:
Матрица – А=(-1) называется противоположной матрице А. Произведение матриц Операция умножения 2-х матриц вводится только для случая когда число столбцов 1 матрицы равно числу строк 2 матрицы. Схематично произведение матриц можно изобразить так:
Пример 1.
Пример 2.
Матрица А - имеет 3 столбца, матрица В- 2 строки. Условие умножения матриц не выполняется, значит операция умножения не выполнима. Рассмотрим произведение
Понятие определителя Определители были изобретены дважды, что в математике встречается не так уж часто. Сначала они были изобретены в Древнем Китае в начале нашей эры - без глубокой теории, но с хорошими правилами практического применения. Учёные этой страны старались скрывать свои открытия от других народов. В результате то, что было открыто или изобретено китайцами, вновь изобреталось в других странах. Великий немецкий учёный Готфрид Вильгельм Лейбниц (1646 – 1716) в 1693 г. ввёл двойные индексы, которые записывал ниже сроки. Лейбниц стремился во всех исследованиях к единым методам. В частности, он хотел создать единообразный метод решения систем линейных уравнений, что и привело его к определителям. Термин «детерминант», иначе говоря «определитель» (от латинского determino – определяю), в нашем смысле ввёл Коши в 1815 г. Ему удалось найти все главные свойства определителей. Дальнейшее развитие теория определителей получила в трудах английских математиков А. Кэли и Дж. Сильвестера (1814 -1897). Первый из них и ввёл поныне употребляемый знак определителя │ │. Определение: Определитель - это число, которое считается для квадратной матрицы по некоторым вполне определенным правилам. Порядок определителя – это порядок квадратной матрицы. Для обозначения определителя квадратной матрицы A пользуются обозначениями Пусть A - произвольная квадратная матрица порядка n. 1. Если n=1, то матрица A состоит из одного числа A и определитель равен этому числу.
2. Если n=2, то для матрицы определитель вычисляется по правилу
или
Дано:
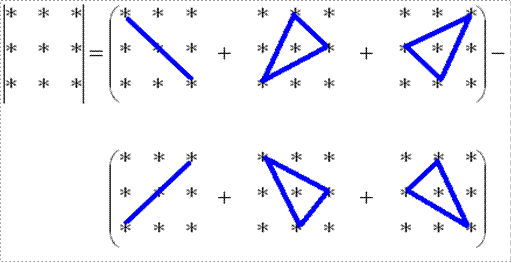
. Решение: 3. Если n=3, то для матрицы
определитель вычисляется по правилу
или
Пример 3: Дано:
detA= detA=9. Метод Крамера 1.4.1 И сторическая справка С развитием теории определителей в конце 17 века швейцарский математик Габриэль Крамер (1704 - 1752) начал разрабатывать свою теорию и в 1751 году, не задолго до своей смерти, опубликовал "правило Крамера" - метод решения систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем матрицы системы. Правило Крамера
(1)
Коэффициенты a11,12,..., a1n,..., an1 , b2,..., bn считаются заданными. Вектор - строка x1, x2,..., xn - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=∆=detA, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи. a). Если D≠0, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера
Рассмотрим частные случаи нахождения решений системы линейных алгебраических уравнений методом Крамера. I.Система уравнений 2-го порядка Запишем систему уравнений 2-го порядка в общем виде
Решение: 1. Построим и вычислим главный определитель системы
2. Построим и вычислим первый вспомогательный определитель системы
3. Построим и вычислим второй вспомогательный определитель системы
Пример 1: Решить систему правилом Крамера
Решение:
Поэтому система имеет единственное решение.
Ответ: x=-1,5; y=2,5. II. Система уравнений 3-го порядка. Запишем систему уравнений 3-го порядка в общем виде
Решение: 1.Построим и вычислим главный определитель системы
2.Построим и вычислим первый вспомогательный определитель системы
тогда 3.Построим и вычислим второй вспомогательный определитель системы
тогда 4.Построим и вычислим третий вспомогательный определитель системы
тогда Пример 9: Решить систему правилом Крамера
Решение:
Поэтому система имеет единственное решение.
Ответ: x=-2; y=1; z=-1. III. Система линейных уравнений с 4-мя неизвестными. Для того, чтобы решить СЛАУ с 4-мя неизвестными необходимо ввести понятия минора определителя и алгебраического дополнения. Определение: Минором Mij к элементу aij определителя n-го порядка называется определитель (n - 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца. Пример 1. Найти миноры матрицы Решение: Минор М22 получается путем вычеркивания строки и столбца на пересечении которых, находится данный элемент, т.е. 2-ой строки 2-го столбца.
Минор М23 получается путем вычеркивания 2 строки и 3-его столбца.
Остальные миноры находятся аналогично.
Введем понятие алгебраического дополнения. Определение: Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число Aij = (-1)i + j · Mij. Если рассмотреть проще, алгебраическое дополнение регулирует знак перед минором. Пример 2. Найти алгебраические дополнения матрицы
ПРАКТИЧЕСКАЯ ЧАСТЬ Решение: Матрицу-строку затрат сырья S можно представить как произведение: S=C*A= (100 80 130)
Общую стоимость сырья можно рассчитать в следующем порядке: вначале рассчитываем матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу:
а затем общую стоимость сырья:
Вывод: Общая стоимость сырья равна 70900 ден. ед, а стоимость затрат сырья на единицу продукции равна Задача 3. Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в таблице. Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Решение. По данным табл. 16.1 составим четыре вектора, характеризующие весь производственный цикл:
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента q на три других вектора, т. е.
Задача 4. Предприятие выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А: Вид сырья 1 2 3 4
Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: соответственно 60, 50, 35 и 40 ед. Решение. Составим вектор-план выпуска продукции Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; этот вектор затрат вычисляется как произведение вектора
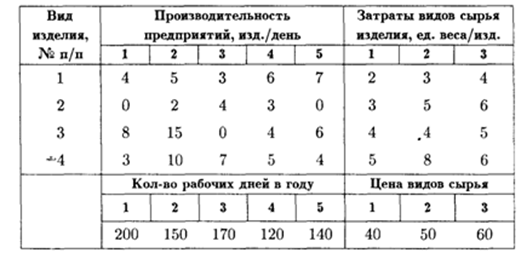
Ответ: Затраты сырья на каждый вид изделия составят 575, 550, 835 и 990 единиц соответственно. Задача 5. Предприятие производит муку трех сортов: ржаную, пшеничную и ячменную и продает ее на 4 региона. Матрица Решение: Выручка предприятия выражается произведением матрицы А на матрицу В. А*В=(200 80 100)* Ответ: Выручка предприятия в 1-ом регионе 680 усл.ед., во 2-ом регионе – 2010 усл.ед.,в 3-ем регионе – 5040 усл.ед., в 4-ом регионе – 1020 усл.ед. Задача 6:. В табл. приведены данные о дневной производительности 5 предприятий, выпускающих 4 вида продукции с потреблением 3-х видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.
Требуется определить: 1) годовую производительность каждого предприятия по каждому виду изделий; 2) годовую потребность каждого предприятия по каждому виду сырья; 3) годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств. Решение: Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи. Прежде всего приведем матрицу производительности предприятий по всем видам продукции: Производительность 1 2 3 4 5
Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность J- го предприятия по каждому виду продукции получается умножением J- гo столбца матрицы А на количество рабочих дней в году для этого предприятия (J = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей:
Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид: Вид изделия 1 2 3 4
Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А: В*А = Где I -я строка соответствует номеру типа сырья, а J- й столбец — номеру предприятия согласно табл. (I = 1, 2, 3; J = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей А год умножением столбцов матрицы ВА на соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья: В*А год = Введем вектор стоимости сырья – Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора Р = Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора Литература 1. Зеленцов Б.П., Кулагина Н.А. Линейная алгебра: Практикум. Новосибирск: Сибирская академия банковского дела и финансов, 2014.-59 с. 2.Красс М.С. Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. Издательство «Дело», 2001. – 688с. 3. Кремер Н.Ш., Путко Б.А.Высшая математика для экономистов:Учебник для вузов. – 2-е изд., М.:ЮНИТИ, 2004-471с. 4.Новикова Т.В.Элементы линейной алгебры и линейного программирования в экономике: Методическая разработка.Издательство «Томинтех»,2013.–53 с. 5.Писменный Д.Т. Конспект лекций по высшей математике. 1 часть. – М.: Айрис-пресс, 2003. – 288 с.
Интернет- ресурсы Ru.onlinemschool.com 2. https://ru.wikipedia.org/wiki/ 3. mathhrofi.ru 4. http://function-x.ru/systems_kramer.html
Элементы линейной алгебры
Разработчик: Есенеева Э.С. ВВЕДЕНИЕ Современная математика характеризуется интенсивным проникновением в другие науки, во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики оказался универсальным, и это есть объективное отражение универсальности законов окружающего нас многообразного мира. Для будущего специалиста любой отрасли изучение математических дисциплин и их экономических приложений, составляющих основу актуальной экономической математики, позволит не только приобрести необходимые базовые навыки, используемые в экономике, но и сформировать компоненты своего мышления: уровень, кругозор и культуру. Одним из основных разделов математики, где широко используются экономические методы решения задач, является раздел «Линейная алгебра». Особенно этот вопрос стал актуальным при разработке и использовании баз данных, так как при работе с ними почти вся информация хранится и обрабатывается в матричной форме. С помощью матриц удобно описывать различные экономические закономерности. Кроме этого около 75% всех расчетных математических задач приходится на решение систем линейных алгебраических уравнений (СЛАУ). Это задачи из области экономики, статистики, электротехники, радиоэлектроники, механики и других. Таким образом, элементы линейной алгебры позволяют описывать те или иные процессы, происходящие в различных сферах деятельности человека. Изучение данного раздела, умение составлять модели процессов с использованием систем линейных уравнений и матриц дает возможность использования полученных знаний в решении конкретных проблем, возникающих в будущей практической профессиональной деятельности. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Понятие матрицы Впервые матрица под названием "волшебный квадрат" упоминается еще в Древнем Китае. Подобные квадраты чуть позже были известны и у арабских математиков. Матрица (размером m x n) - это таблица чисел, содержащая m строк и n столбцов. При этом сами числа называются элементами матрицы, и каждому элементу ставится в соответствие два числа - номер строки и номер столбца. Для обозначения матрицы используются прописные латинские буквы (A, B, C,..), а саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицыобозначают строчными латинскими буквами, снабженными двумя индексами. Например: aij - элемент матрицы А, расположенный в i-й строке и j-м столбце или коротко элемент в позиции ( i,j ). В общем виде матрица размера m на n может быть записана следующим образом
Некоторые экономические зависимости удобно записывать в виде матриц. В пример приведем таблицу распределения ресурсов по отдельным отраслям экономики (в ус. ед). Пример 1:
Эти данные в таблице можно представить в удобной форме в виде матрицы распределение ресурсов по отраслям:
В данном примере, матричный элемент а11 показывает, какое количество электроэнергии потребляет промышленность, а элемент а22 - количество трудовых ресурсов в сельском хозяйстве.
матрица А размером 2 х 4.
матрица B размером 4 x 2.
Элементы aij, где i=j, называются диагональными, а элементы aij, где i≠j - внедиагональными. Определение: Матрица, все элементы которой равны нулю, называется нулевой матрицей. Пример 3:
Определение: Матрица, у которой число строк равно числу столбцов (m=n) называется квадратной матрицей порядка n. Пример 4:
квадратная матрица С порядка 3.
Определение: Матрица размера 1 x n называется матрицей-строкой или вектор-строкой. Матрица размера m x 1 называется матрицей столбцом или вектор-столбцом. Пример 5:
Определение: Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.
Пример 6:
1.2.1 Действия над матрицами. 1. Сложение: Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц
Пример 1:
Аналогично определяется разность матриц. 2.Умножение на число: Произведением матрицы Пример 2:
Матрица – А=(-1) называется противоположной матрице А.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.230.82 (0.175 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
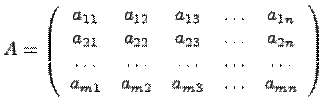
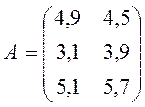
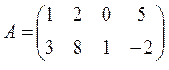 Пример 2:
Пример 2: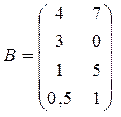
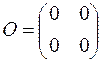 нулевая матрица О.
нулевая матрица О.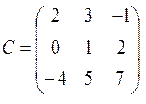
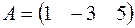 матрица-строка (1х3)
матрица-строка (1х3)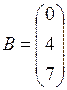 матрица-столбец (3х1)
матрица-столбец (3х1)
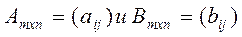 названая матрица
названая матрица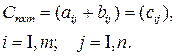
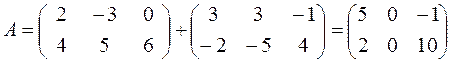
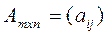 на число k
на число k  называется такая матрица
называется такая матрица 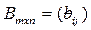 элементы которой равны
элементы которой равны 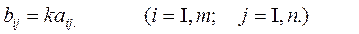
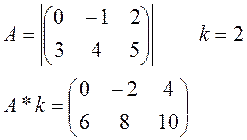





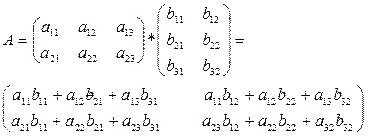 .
.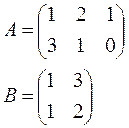 Выяснить определено ли произведение А*В.
Выяснить определено ли произведение А*В.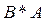 . В матрице В -2 строки, в матрице А – 2 столбца. Операция умножения определена.
. В матрице В -2 строки, в матрице А – 2 столбца. Операция умножения определена.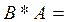
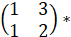
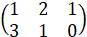
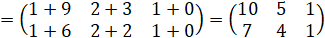 .
.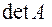 или
или 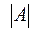 или
или 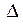 .
.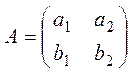 Пример 1:
Пример 1: 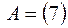 , тогда определитель
, тогда определитель 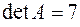
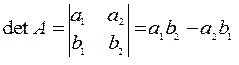
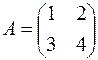 Пример 2:
Пример 2: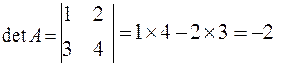
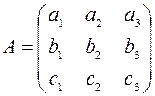
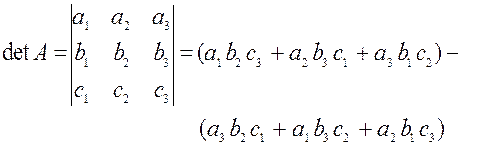
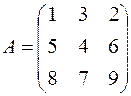
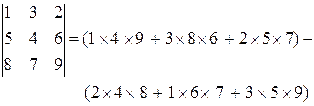 Решение: Определитель матрицы A
Решение: Определитель матрицы A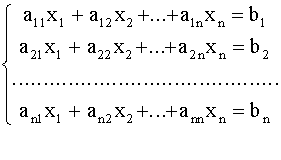 Пусть дана система линейных уравнений
Пусть дана система линейных уравнений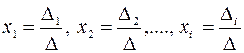 , где
, где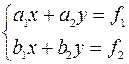
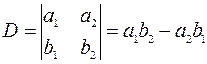
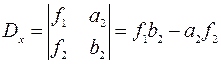 , тогда
, тогда 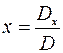
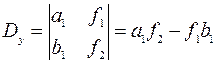 , тогда
, тогда 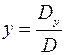
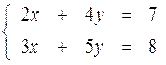
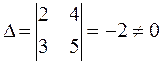
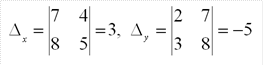

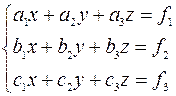
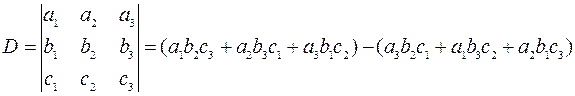
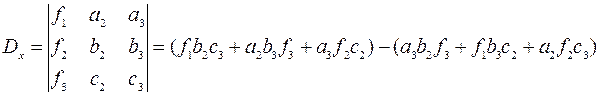 ,
,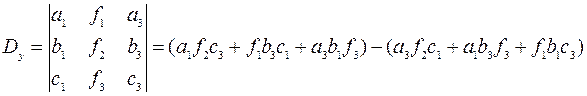 ,
,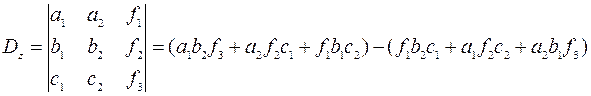 ,
,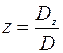
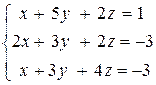
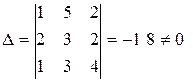
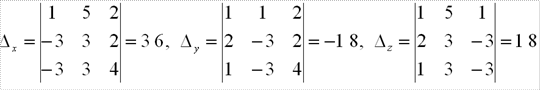
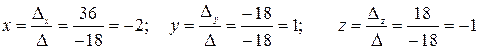
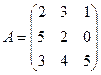 М22, М23.
М22, М23.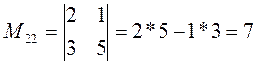
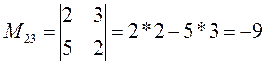 .
.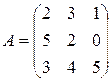 А22, А23 .
А22, А23 .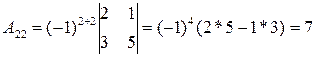
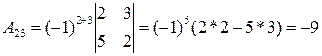 .
.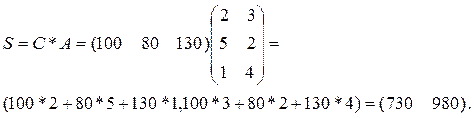
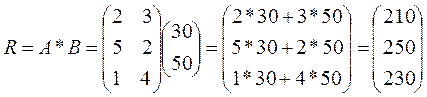
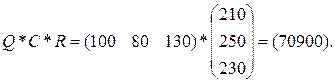
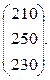
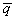 = (20, 50, 30,40) — вектор ассортимента,
= (20, 50, 30,40) — вектор ассортимента,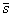 = (5, 2, 7, 4) — вектор расхода сырья,
= (5, 2, 7, 4) — вектор расхода сырья,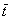 = (10, 5, 15, 8) — вектор затраты рабочего времени,
= (10, 5, 15, 8) — вектор затраты рабочего времени,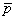 = (30, 15, 45, 20) — ценовой вектор.
= (30, 15, 45, 20) — ценовой вектор.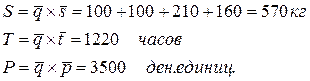
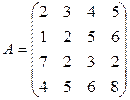
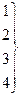 вид изделия
вид изделия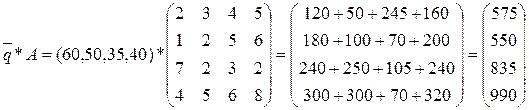
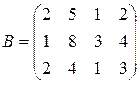 задает цену реализации данной продукции (в усл. ед) i-го сорта в j-м регионе. Определить выручку предприятия в каждом регионе, если реализация муки за месяц (по видам) задана матрицей А (200 80 100).
задает цену реализации данной продукции (в усл. ед) i-го сорта в j-м регионе. Определить выручку предприятия в каждом регионе, если реализация муки за месяц (по видам) задана матрицей А (200 80 100).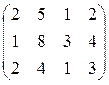 =
= 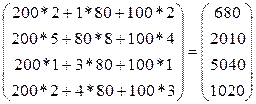
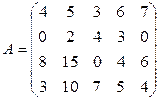
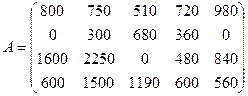
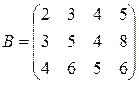
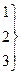 вид сырья
вид сырья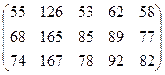
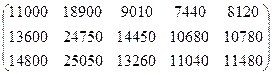
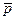 = (40, 50, 60).
= (40, 50, 60).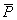 .
.


