
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Габриэль крамер (31 июля 1704 - 04 января 1752) - ученик и друг иоганна бернулли, один из создателей линейной алгебры.
С раннего возраста показал большие способности в области математики. В 18 лет защитил диссертацию. В 20-летнем возрасте Крамер выставил свою кандидатуру на вакантную должность преподавателя на кафедре философии Женевского университета. Он много путешествовал по Европе, заодно перенимая опыт у ведущих математиков - Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне, Мопертюи и Клеро в Париже и других. В свободное от преподавания время Крамер пишет многочисленные статьи на самые разные темы: геометрия, история математики, философия, приложения теории. Термина «определитель» (детерминант) тогда ещё не существовало (его ввёл Гаусс в 1801 году), но Крамер дал точный алгоритм его вычисления. Методы Крамера сразу же получили дальнейшее развитие в трудах Безу, Вандермонда и Кэли, которые и завершили создание основ линейной алгебры. Теория определителей быстро нашла множество приложений в астрономии и механике (вековое уравнение), при решении алгебраических систем, исследовании форм и т.д.
Правило Крамера
(1)
Коэффициенты a11,12,..., a1n,..., an1 , b2,..., bn считаются заданными. Вектор - строка x1, x2,..., xn - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство. Определитель n-го порядка D=∆=detA, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи. a). Если D≠0, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера
Рассмотрим частные случаи нахождения решений системы линейных алгебраических уравнений методом Крамера. I.Система уравнений 2-го порядка Запишем систему уравнений 2-го порядка в общем виде
Решение: 1. Построим и вычислим главный определитель системы
2. Построим и вычислим первый вспомогательный определитель системы
3. Построим и вычислим второй вспомогательный определитель системы
Пример 1: Решить систему правилом Крамера
Решение:
Поэтому система имеет единственное решение.
Ответ: x=-1,5; y=2,5. II. Система уравнений 3-го порядка. Запишем систему уравнений 3-го порядка в общем виде
Решение: 1.Построим и вычислим главный определитель системы
2.Построим и вычислим первый вспомогательный определитель системы
тогда 3.Построим и вычислим второй вспомогательный определитель системы
тогда 4.Построим и вычислим третий вспомогательный определитель системы
тогда Пример 9: Решить систему правилом Крамера
Решение:
Поэтому система имеет единственное решение.
Ответ: x=-2; y=1; z=-1. III. Система линейных уравнений с 4-мя неизвестными. Для того, чтобы решить СЛАУ с 4-мя неизвестными необходимо ввести понятия минора определителя и алгебраического дополнения. Определение: Минором Mij к элементу aij определителя n-го порядка называется определитель (n - 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца. Пример 1. Найти миноры матрицы Решение: Минор М22 получается путем вычеркивания строки и столбца на пересечении которых, находится данный элемент, т.е. 2-ой строки 2-го столбца.
Минор М23 получается путем вычеркивания 2 строки и 3-его столбца.
Остальные миноры находятся аналогично. Введем понятие алгебраического дополнения. Определение: Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число Aij = (-1)i + j · Mij. Если рассмотреть проще, алгебраическое дополнение регулирует знак перед минором. Пример 2. Найти алгебраические дополнения матрицы
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.150 (0.007 с.) |
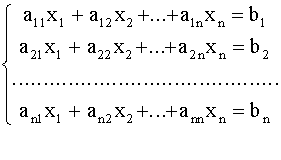 Пусть дана система линейных уравнений
Пусть дана система линейных уравнений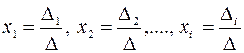 , где
, где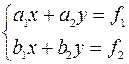
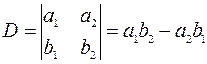
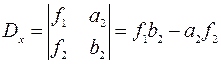 , тогда
, тогда 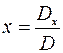
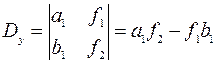 , тогда
, тогда 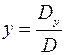
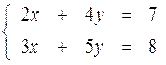
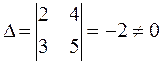
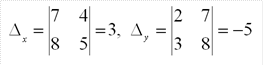

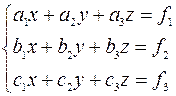
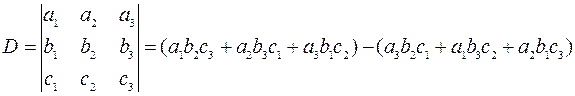
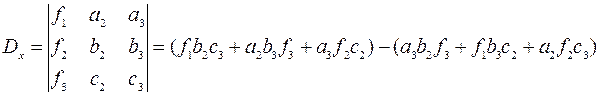 ,
,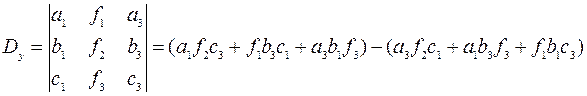 ,
,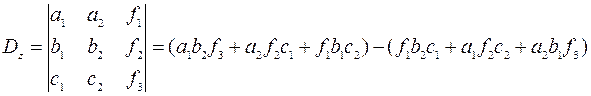 ,
,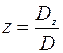
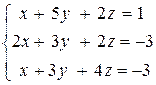
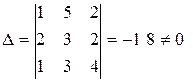
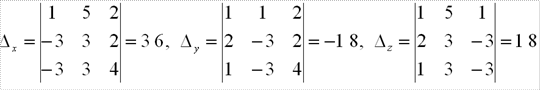
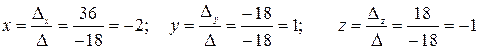
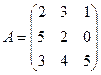 М22, М23.
М22, М23.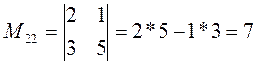
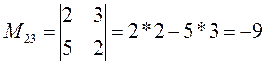 .
.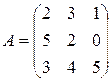 А22, А23 .
А22, А23 .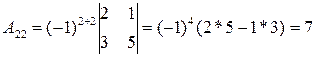
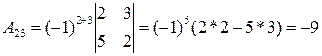 .
.


