
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция поляризованных лучейСодержание книги
Поиск на нашем сайте
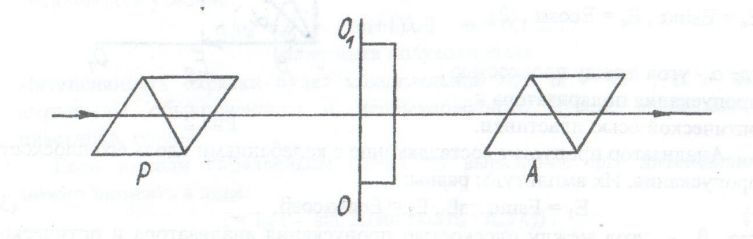
Рассмотрим интерференцию поляризованных параллельных лучей. Поместим между двумя николями пластинку из одноосного двупреломляющего кристалла, вырезанного параллельно оптической оси ОО1 (рис.13). Пусть свет падает на пластинку нормально. Тогда плоскополяризованная волна, вышедшая из поляризатора Р, проходя через пластинку разделится на две волны: обыкновенную и необыкновенную. Так как пластинка вырезана параллельно оптической оси, то обе волны распространяются в пластинке в одном направлении, но с разными фазовыми скоростями. И, следовательно, приобретают оптическую разность хода, которая на выходе из пластинки равна:
где Анализатор А пропускает лишь те составляющие световых векторов обеих волн, которые параллельны его плоскости пропускания. Поскольку обыкновенная и необыкновенная волны когерентны, то когерентны и их составляющие, поляризованные параллельно плоскости пропускания анализатора. Поэтому они интерферируют. Рассчитаем интенсивность света на выходе оптической системы, изображенной на рис. 13, если интенсивность света, выходящего из поляризатора P, равна
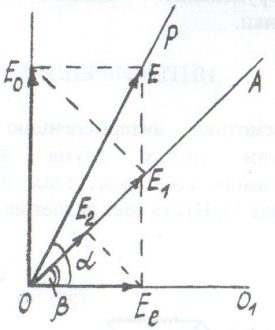
Рис.13. Оптическая система для наблюдения интерференции параллельных лучей На рис. 14 плоскость чертежа перпендикулярна к проходящему через точку O лучу. PO и AO – линии пересечения плоскостей пропускания поляризатора и анализатора соответственно и плоскости чертежа, ОО1 – кристаллическая ось пластинки.
Рис.14. К расчету интенсивности света, выходящего из поляризатора
Пусть амплитуда колебаний светового вектора в луче, вышедшем из поляризатора, равна
где Анализатор пропустит составляющие с колебаниями вдоль его плоскости пропускания. Их амплитуды равны:
где Волны с этими амплитудами когерентны и будут интерферировать после выхода из анализатора. Пусть их разность фаз равна
Тогда амплитуда
Заменяя
В частном случае скрещенных николей:
В этом случае 1) 2) В этом случае, если свет монохроматический, то пластинка, рассматриваемая через анализатор, будет темной. Если же свет белый, то условие минимума (8) будет выполняться лишь для некоторых длин волн и пластинка будет окрашена. Если толщина пластинки всюду одинакова и световой пучок параллелен, то окраска будет однородной. Если толщина пластинки меняется от точки к точке, то будут наблюдаться цветные полосы равной толщины. Главный вклад в окраску пластин даст свет тех длин волн, для которых выполняется условие:
Интенсивность окраски будет максимальной при Если николи параллельны (
Условия максимума и минимума интенсивности света, прошедшего через систему, будут обратными условиям, полученным для случая скрещенных николей. При наблюдении в белом свете будут теперь гаситься те волны, которые давали наибольший вклад в окраску пластинки в случае скрещенных николей. Окраска пластинки будет дополнительной до белой по отношению к той окраске, которую она имела при наблюдении в скрещенных николях. Разность между длинами двух ближайших погашенных волн
т.е. Чем больше
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.153 (0.007 с.) |

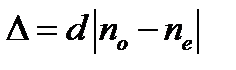 , (15)
, (15)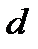 – толщина пластинки;
– толщина пластинки; 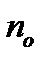 ,
, 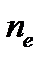 – показатели преломления обыкновенной и необыкновенной волн.
– показатели преломления обыкновенной и необыкновенной волн.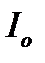 .
.
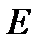 . В кристаллической пластинке этот луч разделится на два. Амплитуды колебаний световых векторов в обыкновенном и необыкновенном лучах
. В кристаллической пластинке этот луч разделится на два. Амплитуды колебаний световых векторов в обыкновенном и необыкновенном лучах 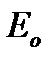 и
и 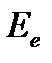 равны:
равны: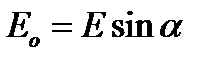 ,
, 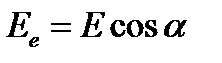 , (16)
, (16)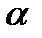 – угол между плоскостью пропускания поляризатора и оптической осью пластинки.
– угол между плоскостью пропускания поляризатора и оптической осью пластинки.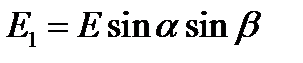 ,
, 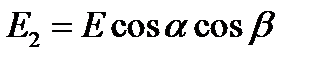 , (17)
, (17)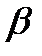 – угол между плоскостью пропускания анализатора и оптической осью пластинки.
– угол между плоскостью пропускания анализатора и оптической осью пластинки.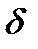 . Она связана с оптической разностью хода соотношением:
. Она связана с оптической разностью хода соотношением: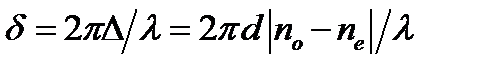 (18)
(18)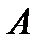 результирующей волны определится формулой:
результирующей волны определится формулой: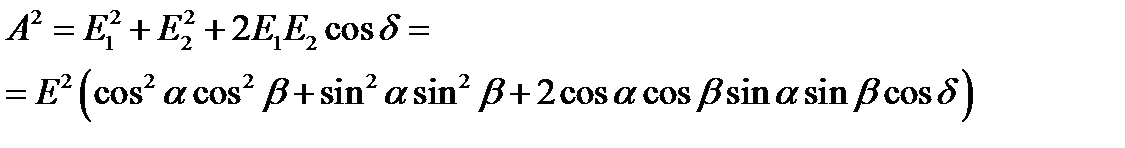 (19)
(19)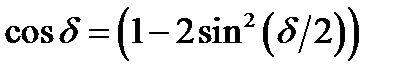 , подставляя выражение (18) для
, подставляя выражение (18) для 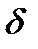 и переходя от амплитуд к интенсивностям, преобразуем формулу к следующему виду:
и переходя от амплитуд к интенсивностям, преобразуем формулу к следующему виду: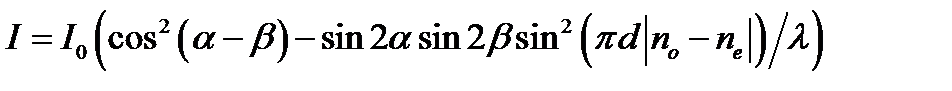 (20)
(20)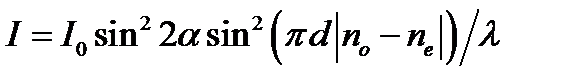 (21)
(21)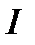 обращается в нуль, если выполняется одно из двух условий:
обращается в нуль, если выполняется одно из двух условий: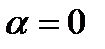 или
или 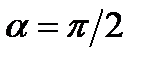 . Это означает, что направление колебаний светового вектора в луче, вышедшем из поляризатора, совпадает с направлением оптической оси пластинки или перпендикулярно к ней, поэтому разложение световой волны на обыкновенную и необыкновенную не происходит. Пластинка, рассматриваемая через анализатор, будет темной, независимо от того: монохроматический или белый свет падает на поляризатор.
. Это означает, что направление колебаний светового вектора в луче, вышедшем из поляризатора, совпадает с направлением оптической оси пластинки или перпендикулярно к ней, поэтому разложение световой волны на обыкновенную и необыкновенную не происходит. Пластинка, рассматриваемая через анализатор, будет темной, независимо от того: монохроматический или белый свет падает на поляризатор. 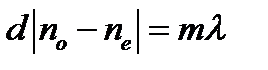 ,
, 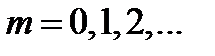 (22)
(22)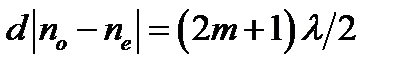 ,
, 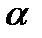 =45º, т.е. когда амплитуды обыкновенного и необыкновенного лучей, вышедших из пластинки равны.
=45º, т.е. когда амплитуды обыкновенного и необыкновенного лучей, вышедших из пластинки равны.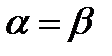 ), то выражение для интенсивности можно записать в виде:
), то выражение для интенсивности можно записать в виде: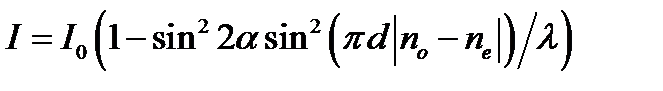 (24)
(24)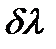 (равная разности между длинами двух ближайших усиленных волн) определяется из условия:
(равная разности между длинами двух ближайших усиленных волн) определяется из условия: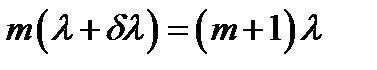 , (25)
, (25)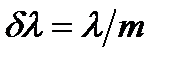 (26)
(26)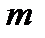 (т.е. чем больше разность хода), тем ближе в спектре располагаются усиливающиеся волны. При достаточно большой разности хода условия максимума интерференции выполняются для многих длин волн и прошедший свет будет казаться почти белым. Таким образом, интерференцию поляризованного света можно наблюдать только при малой разности хода, т.е. в достаточно тонких пластинках.
(т.е. чем больше разность хода), тем ближе в спектре располагаются усиливающиеся волны. При достаточно большой разности хода условия максимума интерференции выполняются для многих длин волн и прошедший свет будет казаться почти белым. Таким образом, интерференцию поляризованного света можно наблюдать только при малой разности хода, т.е. в достаточно тонких пластинках.


