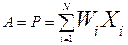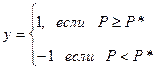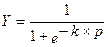Модель искусственного нейрона

 

ИНС – упрощенная модель ткани головного мозга.

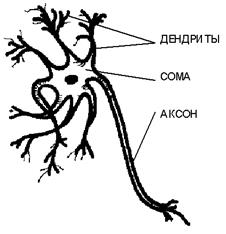
Рисунок 13 – Схема биологического нейрона

 

Нервная клетка состоит из тела (сома, ядро) и отростков (дендриты), по котором в нейрон поступают входные сигналы. Один из отростков служит для передачи выходных сигналов данного нейрона другим нервным клеткам. Он называется аксоном. Соединение аксона с дендритом другого нейрона называется синапсом. Нейрон возбуждается и передает сигнал через аксон, если число пришедших по дендритам возбуждающих сигналов больше числа тормозящих. Принятые синапсом тела сигнала подводится к телу нейрона, причем одни входы стремятся возбудить, другие - напротив.

Каждый нейрон, и искусственный, и естественный, характеризуется функцией преобразования, функцией возбуждения нейрона. Нейроны в сети могут иметь одинаковые или разные функции возбуждения. Сигналы, которые поступают на вход, неравнозначны, информация из одного источника может быть более важной.

Поскольку нейронов много, то нейроны могут иметь различные функции возбуждения.

Сигналы, которые поступают на вход не равнозначны в том смысле, что информация из одного источника может быть более важной, чем из другого источника.

Приоритеты входов задаются с помощью так называемых векторов весовых коэффициентов, моделирующих синоптическую силу биологических нейронов.

 

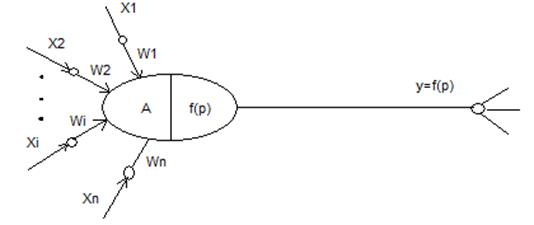
Рисунок 14 – Модель искусственного нейрона

Модель искусственного нейрона представляет собой дискретный преобразователь непрерывной информации.

Это информация, поступающая на вход нейрона, суммируется с учетом весовых коэффициентов сигнала.

n – размерность пространства входных сигналов;

P – потенциал нейрона;

P преобразуется с помощью передаточной функции f(p) и передается другим нейронам сети;

f(p) – активационная функция.

В общем случае эта функция может быть ступенчатой, линейной или нелинейной.

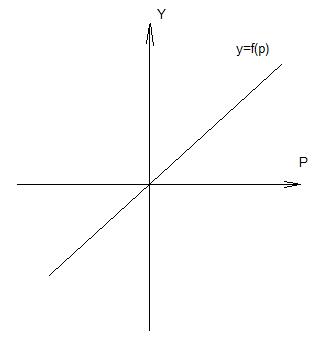
Рисунок 15 – Линейная функция

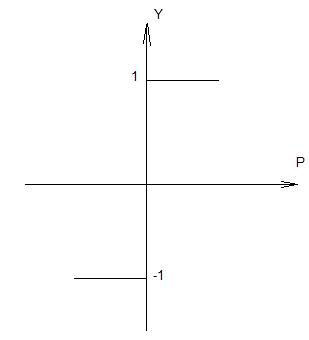
Рисунок 16 – Ступенчатая (пороговая) функция

 

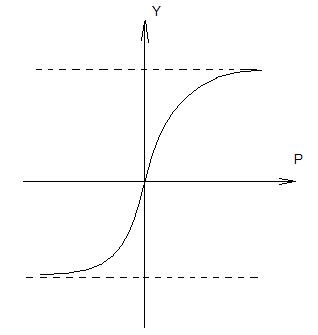
Рисунок 17 – Сигмаидальная (логистическая) функция

 

Пороговая функция пропускает информацию только в том случае, если алгебраическая сумма входных сигналов превышает некоторую величину.

Пороговая функция не обеспечивает достаточной гибкости искусственной нейронной сети в процессе обучения.

Если значение вычислительного потенциала не достигает заданного порога, то выходной сигнал не формируется (не срабатывает).

Это приводит к снижению интенсивности выходного сигнала нейрона и как следствие к формированию невысокого значения потенциала взвешенных входов в следующем слое нейрона.

Линейная функция дифференцирована и легко вычисляется. Это в ряде случаев позволяет уменьшить ошибки выходных сигналов сети, т.е. передаточная функция сети также является линейной.

Однако она не универсальна, т.е. не обеспечивает решение многих задач. Компромиссным решением является сигмаидальная функция.

Эта функция удачно моделирует истинную характеристику биологического нейрона.

Коэффициент k определяет крутизну нелинейной функции.

Подобно ступенчатой функции, сигмаидальная функция позволяет выделять в пространстве признаков различные множества – не выпуклые, не связанные.

При этом сигмаидальная функция не имеет разрывов.

Пик функции переноса выбирается с учетом конкретной задачи, решаемой с применением нейронных сетей.

В задачах аппроксимации и классификации предпочтение отдают логистической (сигмаидальной) функции.

Нейронная сеть представляет собой совокупность искусственных нейронов, организованных слоями – выходы одного нейрона соединяются со входом другого нейрона.

В зависимости от топологии нейрона, нейронные сети подразделяются на:

1) Одно – и многоуровневые;

2) С обратными связями и без.

Связи между слоями могут иметь различную структуру.

В однолинейный сетях каждый нейрон нижнего слоя связан с одним

нейроном верхнего слоя.

    Если каждый нейрон нижнего слоя соединен с несколькими нейронами верхнего слоя, то получается пирамидоидальная сеть.

    Воронкообразная схема предполагает связь каждого узла верхнего слоя со всеми узлами нижнего уровня.

    Чтобы решить конкретную задачу с помощью нейронной сети, нужно выбрать нужный тип соединений нейронов, определить вид передаточных функций элементов и подобрать весовые коэффициенты межнейронных связей.

 

Модели нейронных сетей

 

Разработчики теории – Маккалон и Питтс.

Главные результаты нейронных сетей сводились к следующему:

1. Модель нейрона в виде простейшего процессорного элемента, который вычисляет значение некоторой функции.

2. Конструкция нейронной сети для выполнения логических и арифметических операций.

3. Высказывалось предположение, что нейронная сеть способна обучаться, распознавать образы и обобщать полученную информацию.

Фрэнк Разенблатт (1958 г.) ввел понятие перцептрона – модели

нейронных сетей.

    Разенблатт ввел возможность модификации межнейронных связей. Это сделало нейронную сеть обучаемой.

    Первые перцептроны могли распознавать буквы алфавита.

    Алгоритм обучения перцептрона:

1) Системе предъявляется эталонный образ;

2) Если результат распознавания совпадает с заданным, то весовые коэффициенты не изменяются;

3) Если нейронная сеть неправильно распознает результат, то весовым коэффициентам дается приращение в сторону повышения качества распознавания.

Перцептрон имеет ограниченные возможности, поскольку не всегда

существует такая комбинация весовых коэффициентов, при которой заданное множество образов будет распознаваться правильно.

    Причина в том, что однослойный перцептрон реализует линейную разделенную поверхность пространства эталона, вследствие чего происходит неверное распознавание, если модель не является сепарабельной.

    Сепарабельность – свойство такого пространства, для бесконечного множества элементов которого может быть задан счетный скелет, центр которого обладает центром тяжести, вокруг которого группируются отдельные классы близких по параметрам элементов.

    Пространство является нормированным и для него могут быть определены основные свойства нормированного пространства:

    - метрика;

    - сепарабельность;

    - связность;

    - конформность.

    В метрическом пространстве каждой модели с уникальным набором координат соответствует свой уникальный вектор и единственная точка.

    Малое изменение отдельных координат модели приводит к малым изменениям модели и к малым перемещениям точки.

    Сепарабельность приводит к тому, что все множество элементов пространства может быть разделено на отдельные подмножества моделей, похожих по определенным признакам.

    Конформность означает что объем, заданный некоторым множеством моделей в пространстве, может произвольным образом без разрывов деформироваться в целом или своими локальными частями.

    Связность предполагает, что множество моделей пространства представляет собой единую унитарную структуру в случае односвязности.

    Либо в случае многосвязности, распадается по каким-то признакам на отдельные подмножества.

    Для решения проблем были предложены модели многослойных перцептронов, которые были способны строить ломаную линию.

 

Многослойные сети.

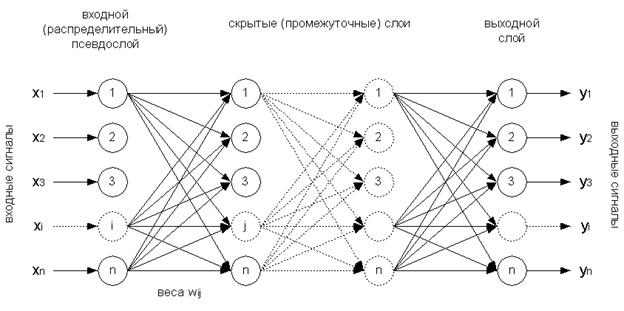
Рисунок 18 - Схема многослойного персептрона

Устанавливаются связи только между нейронами соседних слоев. Каждый слой соединен модифицированной связью с любым нейроном соседних слоев. Между нейронами одного слоя связей нет. Каждый нейрон может посылать сигнал только в вышестоящий слой и принимать выходной сигнал только из нижестоящего слоя. Выходные сигналы подаются на нижний слой, а выходной вектор определяется путем последовательных вычислений уравнений активных элементов каждого слоя снизу вверх с использованием уже известных значений активных элементов предшествующих слоев.

При распознавании образов входной вектор соответствует наибольшему признаку, а выходной- распознаваемым образам:

4-7-4-3

Число нейронов в следующем слое в два раза меньше, чем предыдущем.

Простой персептрон формирует границы области решений в виде гиперплоскости. Двухслойный персептрон выполняет множество функций.

Рекуррентные сети

Эти сети содержат образы связей. Благодаря им становится возможным получать отличные значения при одних и тех же входных данных.

 

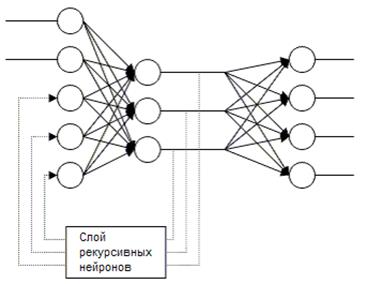
Рисунок 19 - Схема рекуррентной сети

 

Особенность способа заключается в представлении появления новых объектов.

 

Модель Хопфилда

 

В данной модели также используются правила Хебба. Основана на простом предположении, которое заключается в том, если два нейрона возбуждены вместе, то сила связи возрастает, если порознь, то уменьшается связь. Сеть Хопфилда строится с учетом следующих условий:

1. Все элементы связаны со всеми;

2. Прямые и обратные связи симметричны;

3. Диагональные элементы матрицы связей равны 0, т.е. исключаются обратные связи с выходом на входе одного нейрона.

Сеть Хопфилда может выполнять функции ассоциативной памяти,

обеспечивая сходность к тому образу, в область которого попадает начальный образец. Этот подход привлекателен тем, что нейронная сеть запрограммирована без обучения итераций.

Хопфилд выявил функции энергии нейронной сети.

Это функциональное описание поведения сети через стремление к минимуму энергии, которое соответствует заданному набору образов. Веса связей вычисляются на основе вида функции энергии.

Машина Больцмана развивает теорию Хопфилда. Ее предложили Хинтон и Земел. Используется для решения комбинаторных задач. Эти сети получили применение в основе реализации подсистем более сложных. Эти сети также имеют определенные недостатки. Недостатки заключаются в:

1) Предположении о симметричности связи между элементами, без которых нельзя ввести понятие энергии.

2) Нейронная сеть – это устройство для запоминания и обработки информации. Закон энергии играет вспомогательную роль, а не устраивает минимизацию энергии. Сеть Хопфилда поддерживает много лишних связей. В реальности система этого не поддерживает. Происходит освобождение от сильных связей за счет их структуризации. При этом вместо органов связи всех со всеми используется многослойная иерархическая система связи.