
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов. Метод вариации произвольных постоянных.Содержание книги
Поиск на нашем сайте
Общее решение линейного неоднородного дифференциального уравнения
можно представить в виде суммы
где Функция 1) Если Если есть корень характеристического уравнения (29), то частное решение неоднородного уравнения (31) можно искать в виде 2) Если
где Если
где Правая часть Принцип наложения решений. Если правая часть уравнения (31) есть сумма нескольких функций
и
то сумма
является решением уравнения (31). Задача 12. Найти общее решение уравнения
Решение. Характеристическое уравнение определяется выражением
и имеет корни Общее решение однородного уравнения, соответствующего (32), имеет вид
Правая часть уравнения (32)
так как Дифференцируя
Сокращая на
откуда получим
Задача 13. Найти общее решение уравнения
Решение. Характеристическое уравнение
имеет двукратный корень r =1. В данном случае применим принцип наложения решений (суперпозиция). Сначала положим, что правая часть уравнения имеет вид Дифференцируя выражение для
Задача 14. Найти общее решение уравнения
Решение. Характеристическое уравнение
имеет мнимые корни Запишем общее решение однородного уравнения, соответствующего (34) ((30), при
Правая часть (34) относится к виду, описанному в п. 2 неоднородных уравнений:
где
(в нашем случае Дифференцируя
из которой определим
Общее решение
Пример 1. Дано неоднородное линейное уравнение
Используя решение системы: Пусть по-прежнему, правая часть дифференциального уравнения – многочлен. Теперь предположит, что Пример 2. Рассмотрим уравнение
Так как
Пример 3. Дано уравнение
имеет решение Если коэффициент Пример 4. Решим уравнение Фундаментальная система решений
определяется из анализа корней характеристического уравнения
А именно: 1) если
2) если
Задача 15. Решить дифференциальное уравнение
Решение. Составим характеристическое уравнение, которое имеет вид
Решая (38), получим
Корни характеристического уравнения:
Общее решение однородного линейного дифференциального уравнения имеет вид:
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.113.185 (0.009 с.) |


 ,
, – общее решение соответствующего однородного уравнения (28), определяемое по формулам (30);
– общее решение соответствующего однородного уравнения (28), определяемое по формулам (30);  – частное решение уравнения (31).
– частное решение уравнения (31). , где
, где  – многочлен степени
– многочлен степени  .
. не является корнем характеристического уравнения (29) (
не является корнем характеристического уравнения (29) ( и
и  ), то тогда полагают, что
), то тогда полагают, что  , где
, где  – многочлен степени
– многочлен степени  , где
, где  – кратность корня
– кратность корня  или
или  ).
).
 не являются корнями характеристического уравнения, то полагают
не являются корнями характеристического уравнения, то полагают ,
, и
и  – многочлены степени
– многочлены степени  .
. ,
, (для уравнений 2-го порядка
(для уравнений 2-го порядка  уравнения (31) вида 1) или 2) называется специальной правой частью. В общем случае, если правую часть нельзя представить в виде функций 1), 2) или их суммы, для решения уравнения (31) применяется метод вариации произвольных постоянных, описанный в параграфе 5.5..
уравнения (31) вида 1) или 2) называется специальной правой частью. В общем случае, если правую часть нельзя представить в виде функций 1), 2) или их суммы, для решения уравнения (31) применяется метод вариации произвольных постоянных, описанный в параграфе 5.5..

 – соответствующие решения уравнений
– соответствующие решения уравнений ,
, 


 и
и  .
.
 . Разыскиваем частное решение (32) в форме
. Разыскиваем частное решение (32) в форме ,
, и
и  .
.
 и приравнивая друг к другу коэффициенты при первых степенях
и приравнивая друг к другу коэффициенты при первых степенях  и свободные члены в левой и правой частях равенства, имеем
и свободные члены в левой и правой частях равенства, имеем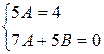
 и
и  ; общее решение данного уравнения есть
; общее решение данного уравнения есть .
.

 ; здесь
; здесь  и
и  , поскольку
, поскольку  , отсюда
, отсюда  дважды, подставляя в уравнение (33) и приравнивая коэффициенты при одинаковых степенях
дважды, подставляя в уравнение (33) и приравнивая коэффициенты при одинаковых степенях  и
и  . Затем положим, что правая часть уравнения
. Затем положим, что правая часть уравнения  , следовательно,
, следовательно,  и
и  . Ищем частное решение в виде
. Ищем частное решение в виде  ; подставляя
; подставляя  в уравнение (33) и производя дифференцирование, получим, что
в уравнение (33) и производя дифференцирование, получим, что  . Следовательно, общее решение дифференциального уравнения (33) определяется выражением
. Следовательно, общее решение дифференциального уравнения (33) определяется выражением


 .
. и
и  )
)
 ,
,  ,
,  . Следовательно, частное решение можно искать в виде
. Следовательно, частное решение можно искать в виде ,
, ,
,  и
и  . В результате получаем следующую систему из четырех уравнений
. В результате получаем следующую систему из четырех уравнений ,
, ,
,  ,
,  . Отсюда частное решение
. Отсюда частное решение
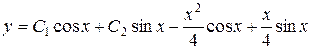 .
. . Характеристическое уравнение
. Характеристическое уравнение  . Поэтому общее решение
. Поэтому общее решение  однородного уравнения будет
однородного уравнения будет  . Теперь для нахождения частного решения
. Теперь для нахождения частного решения  неоднородного уравнения используем метод неопределённых коэффициентов. Полагая
неоднородного уравнения используем метод неопределённых коэффициентов. Полагая  , подставим этот многочлен в исходное уравнение и после упрощения получим:
, подставим этот многочлен в исходное уравнение и после упрощения получим:  .Чтобы найти значения неопределённых коэффициентов, составим систему линейных уравнений, полученную после приравнивания коэффициентов при одинаковых степенях переменной
.Чтобы найти значения неопределённых коэффициентов, составим систему линейных уравнений, полученную после приравнивания коэффициентов при одинаковых степенях переменной  .
. ,
,  ,
,  , получим
, получим  , а затем общее решение исходного уравнения:
, а затем общее решение исходного уравнения:  .
.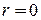 является простым корнем характеристического уравнения. В этом случае ищем
является простым корнем характеристического уравнения. В этом случае ищем  той же степени
той же степени 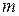 , дополнительно умноженного на переменную
, дополнительно умноженного на переменную  . В противном случае, нам не удастся найти значения неопределённых коэффициентов многочлена
. В противном случае, нам не удастся найти значения неопределённых коэффициентов многочлена  . Используя корни
. Используя корни  ,
,  характеристического уравнения, получим
характеристического уравнения, получим  . Затем найдём частное решение неоднородного уравнения в форме
. Затем найдём частное решение неоднородного уравнения в форме  . Подставим это выражение в исходное уравнение и, приравнивая коэффициенты при одинаковых степенях переменной
. Подставим это выражение в исходное уравнение и, приравнивая коэффициенты при одинаковых степенях переменной  .
. ,
,  , то
, то  , поэтому
, поэтому  .
. . Поскольку характеристическое уравнение
. Поскольку характеристическое уравнение  имеет корни
имеет корни  , то
, то  . Заметим, что
. Заметим, что  не является частным решением характеристического уравнения и будем искать частное решение неоднородного уравнения в форме
не является частным решением характеристического уравнения и будем искать частное решение неоднородного уравнения в форме  . Подставим это выражение в исходное дифференциальное уравнение и получим равенство
. Подставим это выражение в исходное дифференциальное уравнение и получим равенство  . Разделим обе его части на общий множитель
. Разделим обе его части на общий множитель  и приравняем коэффициенты при различных степенях
и приравняем коэффициенты при различных степенях 
 . Таким образом,
. Таким образом,  .
. в показателе экспоненты - корень характеристического уравнения, частное решение следует в виде
в показателе экспоненты - корень характеристического уравнения, частное решение следует в виде  , где
, где 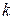 – кратность корня
– кратность корня  . Так как характеристическое уравнение имеет двухкратный корень
. Так как характеристическое уравнение имеет двухкратный корень  , то
, то  . Теперь заметим, что коэффициент
. Теперь заметим, что коэффициент  совпадает с двухкратным корнем характеристического уравнения, поэтому частное решение ищем в виде
совпадает с двухкратным корнем характеристического уравнения, поэтому частное решение ищем в виде  . Подставим это выражение в дифференциальное уравнение и разделим обе его части на
. Подставим это выражение в дифференциальное уравнение и разделим обе его части на  .
. однородного линейного уравнения порядка n с постоянными коэффициентами
однородного линейного уравнения порядка n с постоянными коэффициентами

 , то ему соответствует
, то ему соответствует 
 – пара комплексных корней уравнения (36) кратности
– пара комплексных корней уравнения (36) кратности 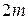 линейно-независимых решений уравнения (35)
линейно-независимых решений уравнения (35)



 . Запишем четыре линейно независимых решения уравнения (37):
. Запишем четыре линейно независимых решения уравнения (37): ,
,  ,
,  ,
,  .
. .
.


