
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
Задачи, приводящие к дифференциальным уравнениям Многие задачи естествознания приводят к нахождению неизвестных функций, описывающих рассматриваемые явления или процессы, когда известны соотношения, связывающие между собой эти функции и их производные. Такие соотношения называются дифференциальными уравнениями. В качестве иллюстрации рассмотрим следующие примеры. Пример 1. Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 секунды после начала замедления, если Решение: примем за независимую переменную время В данном случае Тогда Найдя зависимость скорости от времени, легко найти скорость точки через 3 секунды после начала замедления. Найдем сначала параметры Следовательно, скорость точки изменяется по закону Задача 2. Кривая проходит через точку Решение. Рассмотрим произвольную точку
Рис.1. У гловой коэффициент
где В результате мы получили целое семейство функций, удовлетворяющих критерию задачи. Но в условии есть уточнение: кривая проходит через точку Таким образом, уравнение искомой кривой: Ответ:
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.17 (0.006 с.) |
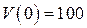 м/с, а
м/с, а 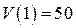 м/с.
м/с.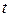 , отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки
, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки 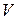 будет функцией от
будет функцией от 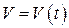 . Для нахождения
. Для нахождения  воспользуемся вторым законом Ньютона (основным законом механики):
воспользуемся вторым законом Ньютона (основным законом механики): 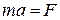 , где
, где 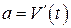 - есть ускорение движущегося тела,
- есть ускорение движущегося тела,  - результирующая сила, действующая на тело в процессе движения.
- результирующая сила, действующая на тело в процессе движения.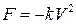 ,
,  – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция
– коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция 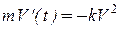 или
или 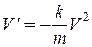 . Здесь
. Здесь 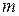 – масса тела.
– масса тела.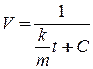 , где
, где 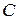 – const.
– const.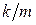 и
и 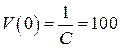 и
и 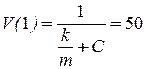 . Отсюда
. Отсюда 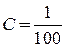 и
и  .
.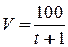 . Поэтому
. Поэтому 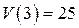 м/с.
м/с.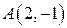 и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности
и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности 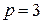 . Найти уравнение этой кривой.
. Найти уравнение этой кривой.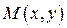 , принадлежащую искомой кривой. На чертеже изобразим некоторую кривую
, принадлежащую искомой кривой. На чертеже изобразим некоторую кривую 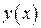 , произвольную точку
, произвольную точку 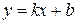 , проведённую к графику функции в данной точке (рис.1).
, проведённую к графику функции в данной точке (рис.1).
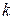 касательной равен тангенсу её угла наклона и равен значению производной в точке
касательной равен тангенсу её угла наклона и равен значению производной в точке 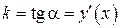 или коротко
или коротко  . По условию, угловой коэффициент касательной
. По условию, угловой коэффициент касательной 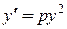 , где
, где 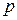 – коэффициент пропорциональности. В данной задаче
– коэффициент пропорциональности. В данной задаче 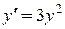 . Решим это уравнение.
. Решим это уравнение.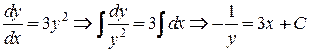 – общее решение,
– общее решение,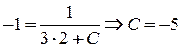 .
.



