
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Фундаментальная система решений.Содержание книги
Поиск на нашем сайте
Функции
Если условие (22) не выполняется, то данные функции называются линейно независимыми. Общее решение однородного линейного дифференциального уравнения
с непрерывными коэффициентами
где Неоднородные уравнения. Общее решение неоднородного линейного дифференциального уравнения
с непрерывными коэффициентами
где Если известна фундаментальная система решений
где искомые функции
Указанный метод называется методом вариации произвольных постоянных. Задача 11. Решить уравнение
Решение. Решая соответствующее (26) однородное уравнение
получим
примем
Ищем решение неоднородного дифференциального уравнения (26) с помощью метода вариации произвольных постоянных, представляя это решение в следующей форме
Составляя систему (25) и учитывая, что приведенный вид исходного уравнения (26) есть
получим
Решая систему (27), определим
отсюда
где
Линейные однородные дифференциальные уравнения 2‑го порядка с постоянными коэффициентами.
Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Ищем решение в виде Пусть сначала к орни
Таким образом, функции
не равен нулю, система функций Пример 1. Решим дифференциальное уравнение. Так как его характеристическое уравнение Пример 2. Дано уравнение Перейдём к случаю, когда корни Пример 3. Дано уравнение Пусть, наконец, корни Пример 4. Решим уравнение Пример 5. Решим уравнение Результаты можно записать в виде таблицы: Пусть
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.215.30 (0.007 с.) |

 ,
, 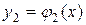 , …,
, …, 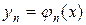 называются линейно зависимыми на
называются линейно зависимыми на 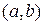 , если существуют постоянные
, если существуют постоянные 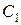 ,
,  , …,
, …, 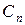 не все равные нулю, такие, что
не все равные нулю, такие, что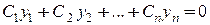 , при
, при 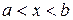

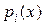
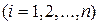 имеет вид
имеет вид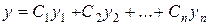
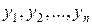 – линейно независимые решения уравнения (23) (фундаментальная система решений).
– линейно независимые решения уравнения (23) (фундаментальная система решений).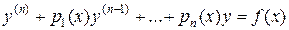
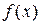 имеет вид
имеет вид ,
, – общее решение соответствующего однородного уравнения (23) и
– общее решение соответствующего однородного уравнения (23) и  – частное решение данного уравнения (24).
– частное решение данного уравнения (24).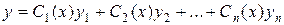 ,
,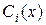
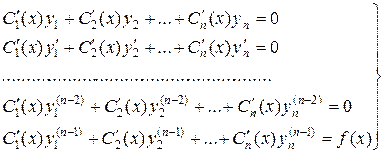
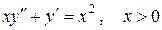
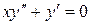 ,
,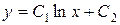
 ,
, 
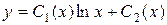


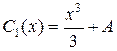 ,
, 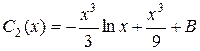
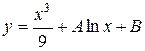 ,
,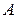 и
и 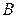 – произвольные постоянные.
– произвольные постоянные.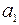 и
и 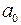 без правой части имеют вид
без правой части имеют вид
 , подставим его в данное уравнение. Полученное алгебраическое уравнение
, подставим его в данное уравнение. Полученное алгебраическое уравнение 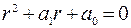 называется характеристическим. Необходимо различать следующие три возможных случая для корней
называется характеристическим. Необходимо различать следующие три возможных случая для корней 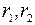 . Рассмотрим их отдельно.
. Рассмотрим их отдельно. . Тогда функции
. Тогда функции 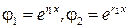 образуют фундаментальную систему решений. Действительно, если r – некоторый действительный корень характеристического уравнения, то подставляя функцию
образуют фундаментальную систему решений. Действительно, если r – некоторый действительный корень характеристического уравнения, то подставляя функцию 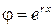 в левую часть дифференциального уравнения, получим равенства
в левую часть дифференциального уравнения, получим равенства .
. являются частными решениями. Так как определитель Вронского
являются частными решениями. Так как определитель Вронского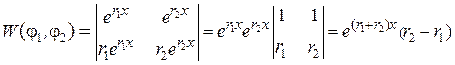
 .
.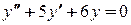 .
.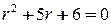 имеет корни
имеет корни 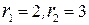 , то фундаментальная система решений будет
, то фундаментальная система решений будет  и общее решение:
и общее решение: 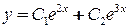 .
.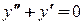 . Его характеристическое уравнение
. Его характеристическое уравнение 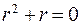 имеет корни
имеет корни 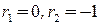 . Заметим, что корню
. Заметим, что корню 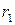 соответствует частное решение
соответствует частное решение  , поэтому общее решение дифференциального уравнения будет
, поэтому общее решение дифференциального уравнения будет  .
.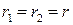 . Другими словами, корень r является двухкратным. Как и для разных корней, можно показать, что фундаментальная система решений имеет вид
. Другими словами, корень r является двухкратным. Как и для разных корней, можно показать, что фундаментальная система решений имеет вид 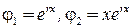 , следовательно,
, следовательно,  - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.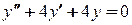 . Его характеристическое уравнение
. Его характеристическое уравнение  имеет двукратный корень
имеет двукратный корень  . Поэтому в качестве фундаментальной системы решений следует выбрать
. Поэтому в качестве фундаментальной системы решений следует выбрать 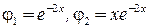 . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид  .
.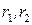 характеристического уравнения - комплексные сопряжённые числа:
характеристического уравнения - комплексные сопряжённые числа:  . В этом случае фундаментальной системой решений:
. В этом случае фундаментальной системой решений: 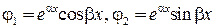 . Общее решение дифференциального уравнения имеет вид
. Общее решение дифференциального уравнения имеет вид 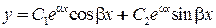 .
.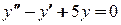 . Решая соответствующее характеристическое уравнение
. Решая соответствующее характеристическое уравнение 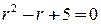 , найдём корни
, найдём корни  . Общее решение дифференциального уравнения:
. Общее решение дифференциального уравнения: 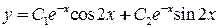 .
. . Здесь корни характеристического уравнения
. Здесь корни характеристического уравнения 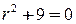 мнимые:
мнимые: 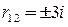 , поэтому
, поэтому 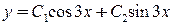 – общее решение.
– общее решение.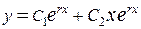 , если
, если 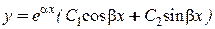 если
если 


