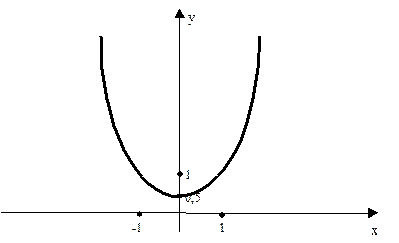Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
Дифференциальное уравнение вида
первой степени относительно
и называется однородным линейным дифференциальным уравнением. В этом случае переменные разделяются и общее решение уравнения (9) можно представить следующим образом
Для решения неоднородного линейного уравнения (8) применим метод вариации произвольных постоянных. Указанный метод состоит в том, что сначала находится общее решение соответствующего однородного уравнения, т.е. соотношение (10). Затем, полагая в (10) величину
Задача 5. Решить уравнение.
Решение. Приведем соответствующее однородное уравнение
Используя (10), получим следующее его решение
Считая
Подставляя
или
откуда
Следовательно, общее решение уравнения (11) имеет вид
Приведем второй способ решения линейного неоднородного уравнения (метод Бернулли). Для решения уравнения (8) можно применить подстановку
где
Потребуем, чтобы
и, разделяя переменные, найдем Уравнение (13) примет вид
Отсюда найдем Задача 6. Решить задачу Коши: Решение. Для простоты сначала разделим обе части уравнения на Ответ: Дифференциальное уравнение 1-го порядка вида
где
Задача 7. Решить уравнение
Решение. Рассматриваемое уравнение является уравнением Бернулли
или
Для определения функции
откуда Подставляя приведенное выше выражение в уравнение (15), получим
Отсюда определим функцию
Следовательно, общее решение имеет вид
Задача 8. Р ешить уравнение Приравняем к нулю выражение в скобках и из общего решения полученного уравнения выберем, например, следующее частное решение Ответ: Задача 9. Для данного дифференциального уравнения
построить интегральную кривую, проходящую через точку Решение. Общим решением является семейство парабол
Из условий в точке
Отсюда искомая интегральная кривая
На рисунке показан график полученной интегральной кривой
Рис.2.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.29.89 (0.011 с.) |
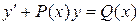
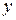 и
и 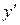 называется линейным. Если
называется линейным. Если  , то уравнение (8) принимает вид
, то уравнение (8) принимает вид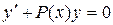

 функцией от
функцией от  , ищем решение неоднородного уравнения (8) в виде (10). Для этого подставляем в уравнение (8)
, ищем решение неоднородного уравнения (8) в виде (10). Для этого подставляем в уравнение (8) 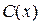 . Таким образом, общее решение неоднородного уравнения (8) получаем в виде
. Таким образом, общее решение неоднородного уравнения (8) получаем в виде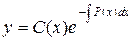
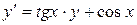


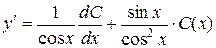


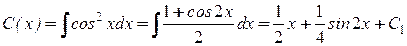
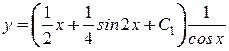
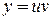 ,
,
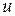 и
и 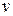 – неизвестные функции от
– неизвестные функции от 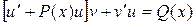
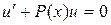

 ,
,  .
. . Приравняв круглую скобку к нулю, затем разделив переменные в
. Приравняв круглую скобку к нулю, затем разделив переменные в 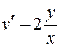 и проинтегрировав результат, получим равенство
и проинтегрировав результат, получим равенство 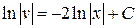 . Выбор значения
. Выбор значения  , приводит к достаточно простой функции
, приводит к достаточно простой функции  . Так как выражение в скобке теперь равно нулю, получим уравнение
. Так как выражение в скобке теперь равно нулю, получим уравнение  , откуда
, откуда 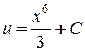 . Общее решение уравнения задачи имеет вид
. Общее решение уравнения задачи имеет вид  . Чтобы найти частное решение, удовлетворяющее начальным условиям, подставим
. Чтобы найти частное решение, удовлетворяющее начальным условиям, подставим 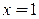 ,
,  в общее решение и получим
в общее решение и получим  .
.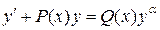 ,
,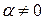 и
и  , называется уравнением Бернулли. Оно приводится к линейному с помощью подстановки
, называется уравнением Бернулли. Оно приводится к линейному с помощью подстановки  . Можно также непосредственно применять подстановку
. Можно также непосредственно применять подстановку  или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной.
 . Подставляем (12) в уравнение (14). В результате получим
. Подставляем (12) в уравнение (14). В результате получим

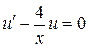 ,
,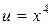 .
.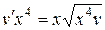 .
. .
. .
. . Полагая
. Полагая  .
. . Подставив его в выделенное равенство, получим уравнение
. Подставив его в выделенное равенство, получим уравнение  с общим решением
с общим решением 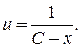
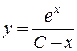 .
.
 .
.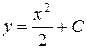
 найдем
найдем