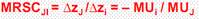Графический анализ предпочтений агента: кривые безразличия

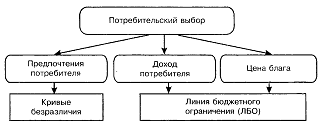
Задача потребителя может быть решена графически в случаях, когда потребительский выбор осуществляется на наборах, включающих не более двух благ

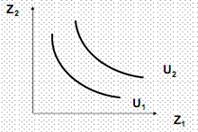
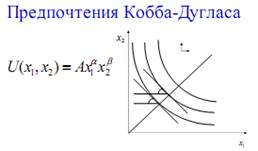
 При этом неважно – положен в основу построений кардиналистический, либо ординалистический подход

Отображением функции полезности (системы предпочтений) являются кривые безразличия, образующие карту безразличия

Кривая безразличия – совокупностьпотребительских наборов, разных по составу, но имеющих одинаковую для данного потребителя полезность (порядок предпочтений)

Карта безразличия – совокупность кривых безразличия для данного типа предпочтений

Предпочтения агента такие, что блага z₁,z₂ рассматриваются как субституты (заменители), описываются функцией полезности Кобба-Дугласа:

U(z₁,z₂) = A z₁^az₂^b, где A=const >0 (рис. 4)

В неоклассической (кардиналистической) функции полезности: 0 < a,b < Такие предпочтения принято называть нормальными

 

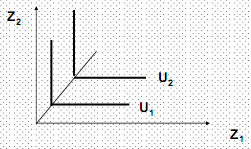
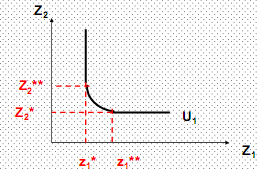
Рис. 4. Кривые безразличия неоклассического типа для благ-субститутов

 

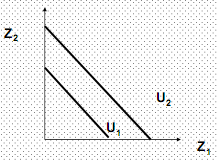
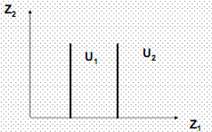
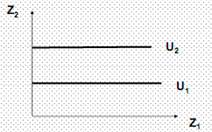
Аддитивная функция полезности также отражает отношение агента к благам как к субститутам: U (z ₁, z ₂) = az ₁ + bz ₂,

где a - предельная полезность первого блага,

b – предельная полезность второго блага

Если a=const и b=const, закон убывающей предельной полезности не выполняется, в этом случае предпочтения называют вырожденными (рис. 5).

Рис. 5. Кривые безразличия для благ-субститутов с постоянными предельными полезностями

 

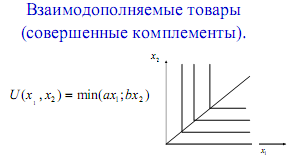
Предпочтения агента, потребляющего блага совместно, т.е. относящегося к благам как к комплементариям, описываются функцией полезности Леонтьевского типа:

U (z ₁, z ₂) = min { az ₁; bz ₂ }

Здесь параметр a - предельная полезность первого блага, параметр b – предельная полезность второго блага

Рис. 6. Кривые безразличия для благ-комплементариев

Рис. 7.а. Кривые безразличия для благ-индифферентов: агент безразличен ко второму благу (z2)	Рис. 7.б. Кривые безразличия для благ-индифферентов: агент безразличен к первому благу (z1)

Рис. 8. Кривая безразличия для случая ограниченной субституции: заменяемость возможна только в рамках зоны субституции

 

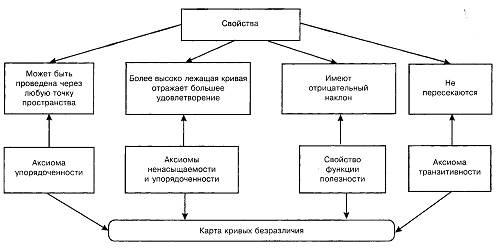
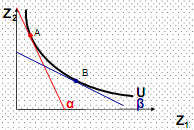
Принято нумеровать кривые безразличия от начала координат

Больший индекс кривой безразличия соответствует более высокому уровню полезности (порядку предпочтения):

U_{k +1} > U_k

Свойства кривых безразличия:

v каждой кривой безразличия соответствует определенный уровень полезности (порядок предпочтения)

v чем дальше от начала координат находится кривая безразличия, тем большую полезность имеют составляющие ее наборы (следствие ненасыщаемости)

v кривые безразличия не пересекаются (каждый набор имеет определенную полезность, или порядок предпочтения)

v кривые безразличия для нормальных предпочтений выпуклы относительно начала координат, или: касательные к кривым безразличия имеют отрицательный наклон.

Важнейшей характеристикой кривых безразличия для благ-субститутов является предельная норма замещения в потреблении (коэффициент субституции) – MRSC_ji

MRSC_ji показывает пропорцию замены i -го блага j -ым без изменения полезности набора.

MRSC всегда определяется для конкретного набора.

Различные наборы имеют разную предельную норму замещения в потреблении. Исключение составляют случаи вырожденных предпочтений.

Пропорция замены j-ым благом i-го блага определяется, исходя из неизменности полезности набора:

U = const или dU = 0

dU = dU_J + dU_i = ∆ z_J ∙ MU_J + ∆ z_i ∙ MU_i = 0 Þ

Предельная норма замещения в потреблении (по модулю) является убывающей функцией заменяемого блага (z_i) и возрастающей функцией заменяющего блага (z_J)

|MRSC_Ji| = φ (z_i,z_J):

∂φ / ∂z_i < 0

∂φ / ∂z_J > 0

На рис. 9 показаны величины MRSC₂₁:

для набора А - тангенс угла наклона касательной к кривой безразличия в точке А (tg α)

MRSC₂₁ для набора В – тангенс угла наклона касательной в точке В (tg β)

|tg a| > |tg β|

Рис. 9. Определение предельной нормы замещения в потреблении