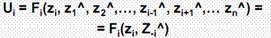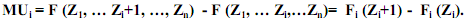Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
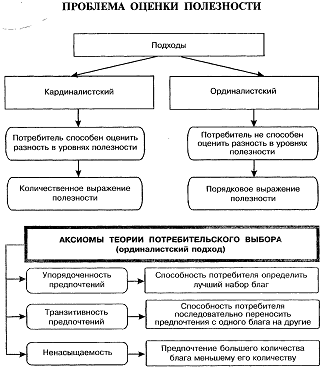
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция полезности набора ( U ) показывает зависимость удовлетворения агента от количеств благ, присутствующих в наборе:Содержание книги
Поиск на нашем сайте
U = F (Z 1, Z 2, … Zn). Функция (общей) полезности набора отражает систему предпочтений конкретного агента, а также взаимосвязь благ в потреблении Многообразие предпочтений потребителей Þ многообразие функций полезности, описывающих эти предпочтения Основные типы функций полезности: v функция полезности Кобба-Дугласа (нормальные предпочтения, блага - субституты): U(Zn) = Z1a1 Z2a2… Znan v аддитивная функция полезности (вырожденные предпочтения; блага - субституты): U(Zn) = a1Z1 + a2Z2 +…+ anZn v функция полезности Леонтьевского типа (блага – комплементарии): v U(Zn) = min {a1Z1; a2Z2;…; anZn} Свойства функции полезности: 1. 2. 3. 4. 5.
Кардиналисты: ü полезность измерима ü важен уровень полезности, доставляемый агенту благом или набором благ ü функция полезности (U(Zn)) определена однозначно Функция полезности блага i-го вида показывает зависимость удовлетворения агента от количества этого блага при прочих равных условиях (неизменном количестве других благ в наборе):
Предельная полезность блага i -го вида – функция, показывающая изменение полезности набора при изменении количества данного блага в наборе на единицу:
Если благо делимо на бесконечное количество частей (непрерывно), функция полезности также непрерывна Тогда: MUi =∂ U (Zn) / ∂ zi Закон убывающей предельной полезности: каждая последующая единица блага имеет полезность меньшую, чем предыдущая В основе закона – тезис о поэтапности удовлетворения потребностей: по мере потребления блага степень интенсивности потребности снижается
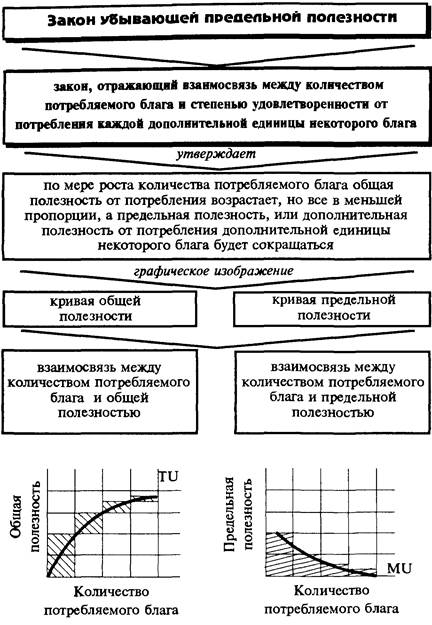
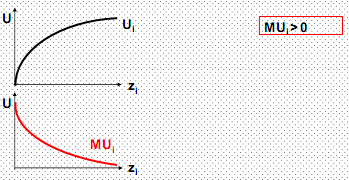
Увеличение количества i -го блага в наборе обусловливает: v увеличение общей полезности набора (по крайней мере, до насыщения потребности): ∂U /∂zi = MUi > 0, if zi < zi* v уменьшение предельной полезности i-го блага: ∂MUi /∂zi = ∂2Ui /∂zi2 < 0 Динамика общей и предельной полезности i -го блага для трех случаев: · насыщение невозможно (рис.1) · потребность в благе может быть полностью удовлетворена (рис. 2) · возможно перенасыщение – благо становится анти-благом (рис. 3)
Рис. 1. Общая и предельная полезность блага (насыщение невозможно)
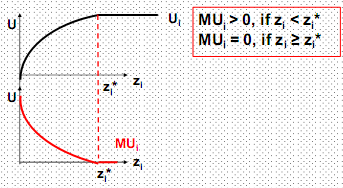
Рис. 2. Общая и предельная полезность блага (потребность в благе может быть полностью удовлетворена)
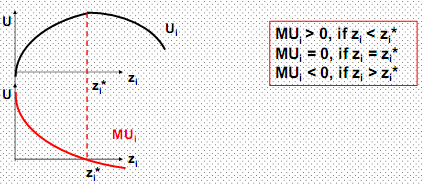
Рис. 3. Общая и предельная полезности блага (возможно перенасыщение) В кардиналистической версии теории предельной полезности функция полезности набора определялась дискретно Полезность набора определялась как сумма полезностей благ, входящих в набор
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.006 с.) |

 – возрастающая функция
– возрастающая функция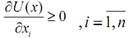
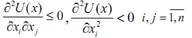
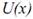 для данной системы не единственна. Она вводится с точностью до монотонно возрастающего преобразования
для данной системы не единственна. Она вводится с точностью до монотонно возрастающего преобразования