Правила перевода чисел из одной системы счисления в другую

 

(Слайд).Для перевода чисел из системы счисления с основанием q в систему счисления с основанием р могут быть использованы следующие методы:

метод непосредственного замещения (для перевода целых, дробных и смешанных чисел);

метод последовательного деления на основание новой системы счисления (только для перевода целых чисел);

метод последовательного умножения на основание новой системы счисления (только для перевода правильных дробей).

 

Перевод чисел с использованием метода непосредственного замещения

 

(Слайд). Перевод чисел рассмотрим на примерах.

Пример 1:                  A ₍₁₀₎ = 35,25 ® A ₍₂₎

35,25₍₁₀₎ = 3×10¹ + 5×10⁰ + 2×10^-1 + 5×10^-2;

A ₍₂₎» 100011,01.

Пример 2:                  A ₍₂₎ = 1001,011 ® A ₍₁₀₎

1001,011₍₂₎ = 1×10³ + 0×10² + 0×10¹ + 1×10⁰ + 0×10^-1 + 0×10^-2 +1×10^-3;

A ₍₁₀₎ = 1×2³ + 0×2² + 0×2¹ + 1×2⁰ + 0×2^-1 + 1×2^-2 + 1×2^-3;

A ₍₁₀₎ = 9,375.

 

Метод непосредственного замещения удобен при переводе чисел из любой CC в ту СС, в которой наиболее просто выполняются арифметические операции. При ручном счете этим методом удобно переводить числа в десятичную СС, а при автоматическом переводе с помощью ЭВМ – в двоичную СС.

 

Перевод из десятичной системы в любую другую. Перевод целых чисел

 

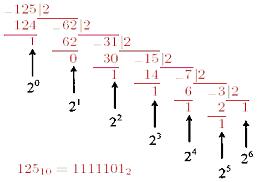
(Слайд).Целое десятичное число нужно поделить на основание новой системы счисления.Остаток от этого деления является самым младшим разрядом в новой записи числа.Результат деления вновь делится на основание.Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т. д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления – самым старшим разрядом в новой записи числа.

Проверка перевода осуществляется по формуле (1.2), так, как это показано ниже на примерах.

Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (1.2). (Слайд).

 

 

(Слайд). Проверка:

*в двоичном коде:

*в восьмеричном коде:

*в шестнадцатеричном коде:

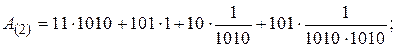
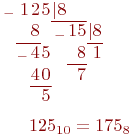
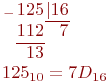
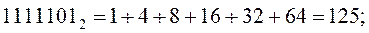
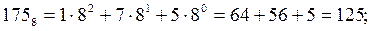
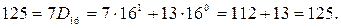
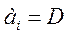В рассмотренном примере при переводе вместо коэффициента  используется его десятичный эквивалент  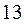в соответствии с таблицей 1.3. (Слайд).

 

Таблица 1.3 – Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15