
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип представления чисел в позиционных системах счисления.Содержание книги
Поиск на нашем сайте
Введение. Принцип представления чисел в позиционных системах счисления. Правила перевода чисел из одной системы счисления в другую.
Учебная литература: [1], [2], [6], [7], [8], [11].
Введение
«Цифровые устройства и микропроцессоры в радиоэлектронном оборудовании» относится к числу основополагающих дисциплин в системе подготовки авиационных специалистов с высшим образованием для специальности: 1-37 04 02 «Техническая эксплуатация авиационного оборудования»; направления специальности: 1-37 04 02-02 «Техническая эксплуатация авиационного оборудования (радиоэлектронное оборудование)» для качественной и безаварийной эксплуатации авиационной техники. (Слайд).Цели учебной дисциплины: изучение основ цифровой техники, общего устройства микропроцессоров, микроконтроллеров, микрокомпьютеров, принципов организации обмена информацией и методов построения систем на их основе, используемых для цифровой обработки сигналов. Основной задачей дисциплины является подготовка курсантов к правильной эксплуатации авиационной техники на основе полученных знаний в области цифровой техники и цифровой обработки сигналов в радиоэлектронном оборудовании. (Слайд). В соответствии с учебным планом на изучение учебной дисциплины отводится 312 часов, в том числе аудиторных – 176 часов. Распределение аудиторного времени по видам занятий и семестрам: в 6-ом семестре – 106 часов аудиторных занятий, из них: лекции – 70 часов, практические занятия – 36 часов; в 7-ом семестре – 70 часов аудиторных занятий, из них: лекции – 48 часов, практические занятия – 22 часа. При изучении данной дисциплины используются такие формы текущей аттестации как курсовой проект, контрольная работа 7-ом семестре, экзамен по учебной дисциплине в 6-ом и 7-ом семестрах. К экзамену допускаются курсанты, выполнившие все требования учебной программы, получившие положительную оценку по комплексной контрольной работе, зачеты по практическим занятиям и защитившие курсовой проект. В результате изучения дисциплины курсанты должны (Слайд). ЗНАТЬ: · арифметические и логические основы вычислительной техники; · общую структуру и принцип функционирования микропроцессорных систем (МПС); · организацию и режимы работы микропроцессоров (МП) и микроконтроллеров (МК); · элементы программирования МП и МК; · особенности применения МПУ в РЭО; · основные этапы разработки МПС на основе МК и МП. (Слайд). УМЕТЬ: · работать с учебной и научно-исследовательской литературой; · обоснованно выбирать архитектурные и структурные решения МПС; · рационально распределять выполняемые МПС функции между аппаратурой и программным обеспечением (ПО); · оптимизировать используемые технические средства при построении МПУ. БЫТЬ ОЗНАКОМЛЕНЫ: · с тенденциями развития МК, МП и МПС; · с методикой использования литературных источников и справочников по тематике дисциплины. Применение микропроцессоров и микроЭВМ в радиоэлектронной аппаратуре привело к расширению функциональных возможностей этой аппаратуры, улучшению качества обработки информации, повышению надежности и стабильности функционирования. Поэтому понятно, что современному радиоинженеру необходимы знания и в области микропроцессорной техники и в программировании радиотехнических задач на языках различных уровней.
Порядок проведения, посещения занятий и другие организационные вопросы. ЛИТЕРАТУРА (Слайд). ОСНОВНАЯ: 1. Микушин А.В. и др. Цифровые устройства и микропроцессоры/А.В.Микушин, А.Н.Сажнев, В.И.Сединин. – СПб.: БХВ-Петербург, 2010. – 832 с. 2. Угрюмов Е.П. Цифровая схемотехника/Е.П. Угрюмов. Учебное пособие для вузов. – 2-е изд., перераб. и доп. – СПб.: БХВ-Петербург, 2005. – 800 с. 3. Безуглов Д.А. и др. Цифровые устройства и микропроцессоры/Д.А.Безуглов, И.В. Калиенко. – Ростов-на-Дону: Феникс, 2006. – 480 с. 4. Новиков Ю.В. и др. Основы микропроцессорной техники/Ю.В.Новиков, П.К.Скоробогатов. – 4-е изд., испр.–М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2009. – 357 с. 5. Корячко В.П. Микропроцессоры и микроЭВМ в радиоэлектронных средствах/ В.П.Корячко. Учебник для вузов.– М.: Высшая школа, 1990. – 407 с.
(Слайды). ДОПОЛНИТЕЛЬНАЯ: 6. Музылева И.В. Основы цифровой техники. Курс лекций/И.В. Музылева. – М.: Университет «ИНТУИТ». [Электронный ресурс]. – 2011. – Режим доступа: http://ИНТУИТ.RU. 7. Пономарев И.А., Панченко Ю.Н. Конспект лекций по учебной дисциплине «Цифровые устройства и микропроцессоры»/ И.А.Пономарев, Ю.Н.Панченко. Ч.1: Учебное пособие для учебных заведений гражданской авиации I-III уровня аккредитации. – Кривой Рог: КК НАУ, 2006. – 47 с. 8. Калабеков Б.А. Цифровые устройства и микропроцессорные системы/Б.А.Калабеков. Учебник для техникумов связи. – М.: Горячая линия-Телеком, 2007. – 336 с. 9. Полуянов М.И. Бортовые цифровые вычислительные устройства и машины/М.И.Полуянов. Методическое пособие и задания на практические занятия. – Мн.: МГВАК, 2009. – 86 с. 10. Полуянов М.И. Бортовые цифровые вычислительные устройства и машины/ М.И.Полуянов. Лабораторный практикум. – Мн.: МГВАК, 2010. – 55 с. 11. Лапука О.Г. Бортовые цифровые вычислительные машины и системы/О.Г.Лапука. – Минск: УО ВА РБ, 2007. – 354 с. 12. Ушкар М.Н. Микропроцессорные устройства в радиоэлектронной аппаратуре/Под ред. Б.Ф.Высоцкого. – М.: Радио и связь, 1988. – 128 с. 13. Сергеенко А.Б. Цифровая обработка сигналов/А.Б.Сергиенко. – СПб.: Питер, 2006. – 608 с. 14. Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритм цифровой обработки/В.В.Лосев. Учебное пособие для студентов радиотехнических специальностей вузов. – Мн.: Вышэйшая школа, 1990. – 67 с.
Любая форма человеческой деятельности, функционирование любой из организованных систем (как искусственных, так и естественных) немыслимы без обработки информации. Понятие информация, в этом случае, означает совокупность данных, сведений подлежащих хранению, обработке и передаче. Для управления современным самолетом используется разнообразная и в большинстве случаев быстроизменяющаяся информация. Возможности летчика-оператора по ее правильному восприятию и переработке ограничены, особенно в условиях дефицита времени. Все возрастающие объемы информации при ограниченном времени ее переработки обуславливают широкое внедрение средств автоматизированной обработки, основным элементом которых являются бортовые вычислительные машины (БВМ). В зависимости от формы представления информации БВМ делятся на два класса: аналоговые и цифровые (дискретные). (Слайд). В настоящее время все более широкое применение в авиационном радиоэлектронном оборудовании (РЭО) (в системах связи, радиолокации, при обработке речевых сигналов, изображений и др.) находят цифровые ЭВМ, имеющие по сравнению с аналоговыми ряд преимуществ, таких как: - более высокая надежность; - стабильность параметров при воздействии дестабилизирующих факторов; - высокая точность обработки информации; -значительное сокращение трудоемкости и упрощение операций регулировки и настройки; - возможность создания микросхем с очень высокой степенью интеграции. Успехи в области разработки быстродействующих элементов цифровой техники позволили создать бортовые ЦВМ (БЦВМ), выполняющие десятки миллионов арифметических операций в секунду. (Слайд). Принципиально новые возможности открывает применение цифровых интегральных схем в радиосвязи. Так, использование цифровых синтезаторов частоты позволило существенно снизить аппаратурные затраты и повысить фазовую стабильность генерируемых сигналов. Обработка сигналов цифровыми методами позволяет обеспечить высокую точность, стабильность параметров и получить характеристики, не достижимые аналоговыми методами. В частности, обеспечение очень высокой прямоугольности амплитудно-частотной характеристики (АЧХ) фильтра на аналоговых элементах практически невозможно. Цифровые же фильтры позволяют реализовать произвольную форму АЧХ, в том числе и сколь угодно близкую к прямоугольной. Цифровая схемотехника интенсивно внедряется и в радиоприемную аппаратуру, главным образом в системы управления. В частности, беспоисковая настройка приемника на любую из принимаемых частот осуществляется набором на пульте управления соответствующего кода, предварительно занесенного в устройство памяти. Используя электронные таймеры, также выполняемые на цифровых интегральных микросхемах, можно обеспечить последовательную перестройку радиостанции по любой заранее заданной программе. При этом указанная программа может долговременно храниться в памяти и при отключенном питании. Возможно также управление режимом работы приемника (коэффициентом усиления, полосой пропускания, диаграммой направленности антенны и т. п.). Является перспективным внедрение цифровой техники и в оптико-локационные и телевизионные системы. Цифровое телевидение позволяет повысить качество передачи сигналов благодаря существенному уменьшению накопления искажений в цифровых линиях связи по сравнению с аналоговыми, а также за счет применения специальных способов кодирования, обнаруживающих и исправляющих ошибки передачи информации. Сигналы представленные в цифровой форме, практически не подвержены амплитудным и фазовым искажениям, что позволяет передавать телевизионную информацию на большие расстояния с сохранением ее высокого качества. В результате использования методов и устройств цифровой техники становится возможным длительный бесподстроечный режим работы. С помощью цифровых устройств обеспечивается кодирование сигналов командных радиолиний управления, что обеспечивает высокую помехозащищенность и скрытность передаваемых сообщений. Широкое применение средств цифровой вычислительной техники в бортовых радиоэлектронных комплексах позволяет значительно повысить безопасность полетов. Однако это предъявляет высокие требования к уровню подготовки авиационных радиоинженеров в области цифровой вычислительной техники. Дать основы такой подготовки ставит своей целью дисциплина «Цифровые устройства и микропроцессоры в радиоэлектронном оборудовании».
Системах счисления
(Слайд).Система счисления – это совокупность правил записи чисел цифровыми знаками. Каждому числу А или каждой цифре d в записи числа А можно сопоставить некоторый количественный эквивалент, выражаемый числом. Системы счисления бывают позиционные (ПСС) и непозиционные (НПСС). В настоящее время и в технике, и в быту широко используются как позиционные, так и непозиционные системы счисления. Примерами ПСС и НПСС являются, соответственно, десятичная и римская системы счисления. Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа. В противном случае систему счисления называют непозиционной. Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам "единицы", "десятки", "сотни", "тысячи", "десятые", "сотые", "тысячные" и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного
Аналогично любое число
где n – количество знаков в целой части числа; m – количество знаков в дробной части числа;
(Слайд). Совокупность п + m = r разрядов, используемое для записи числа, с указанием положения запятой, образует разрядную сетку (рисунок 1.1). Количество возможных вариантов значения коэффициента Основание системы счисления – это число, равное количеству знаков, которые используются в этой системе для записи чисел. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием.
Рисунок 1.1 – Разрядная сетка для записи числа
В таблице 1.1 прослеживается аналогия между позиционными системами счисления. (Слайд).
(Слайд). Для числа в системе счисления с основанием
С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности – это совокупность логических схем. Для представления каждой цифры любого алфавита отводится определенный поддиапазон некоторой физической переменной. За счет помех и погрешностей измерения возникают ошибки представления информации этой переменной. Эти ошибки минимальны при двоичном алфавите. (Слайд). Существует также двоично-десятичная система счисления, которая является гибридной. В этой системе цифры десятичной системы счисления представлены в виде двоичного кода. Для этой цели под каждый разряд десятичного числа отводится четыре разряда двоичного числа. Запись и чтение чисел в двоично-десятичной системе счисления поясним на примерах. Пример 1. Записать число 1983 в двоично-десятичной системе счисления. Для этого каждый знак числа в десятичной системе счисления представляем в виде четырехразрядного двоичного кода (рисунок 1.3) и записываем полученное выражение в ряд: 1983 ® 0001100110000011.
Рисунок 1.3 – Переход от десятичной к двоично-десятичной записи числа
(Слайд).Пример 2. Прочитать число, записанное в двоично-десятичной системе счисления 1000010010010101. Для прочтения числа необходимо разделить его на декады, начиная с младшего (самого правого) разряда, по четыре разряда двоичного числа в каждой. Далее прочитать результат для каждой декады в виде цифры десятичной системы счисления (рисунок 1.4).
Рисунок 1.4 – Результат преобразования: 8495
Двоично-десятичная система широко используется в контрольно-проверочной аппаратуре самолетных ответчиков СО-69, СО-73 и других устройствах, в которых информация о десятичном числе записана в виде двоичного кода. (Слайд). На практике часто возникает проблема компактной записи двоичных чисел. Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы Итак, далее мы подробно рассмотрим именно эти позиционные системы – двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления. (Слайд). Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (1.2). Для двоичного числа:
Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системе записываются с указанием основания, десятичные – без этой записи. Для восьмеричного числа:
Для шестнадцатеричного числа:
(Слайд). Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента Из рассмотренных примеров видно, что общая формула (1.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную. Таким образом, в вычислительной технике наиболее распространены: двоичная (BIN), десятичная (DEC), шестнадцатеричная (HEX) и непозиционная двоично-десятичная (BCD) системы счисления. В BCD системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая цифра i-го разряда кодируется 4-мя двоичными цифрами. Восьмеричная СС (OCT) применяется реже. (Слайд). В таблице 1.2 приведены значения некоторых чисел в различных СС.
Таблица 1.2 – Запись чисел в различных ПСС
Основание ПСС | |||||||||||||||||||||||||||||||||||||||||||
| p = 10 (DEC) | p = 16 (HEX) | р = 8 (OCT) | p = 2 (BIN) | p = "2 - 10" (BCD) | ||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 000 | 0000 | ||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1 | 001 | 0001 | ||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | 2 | 010 | 0010 | ||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | 3 | 011 | 0011 | ||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | 4 | 100 | 0100 | ||||||||||||||||||||||||||||||||||||||||
| 5 | 5 | 5 | 101 | 0101 | ||||||||||||||||||||||||||||||||||||||||
| 6 | 6 | 6 | 110 | 0110 | ||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | 7 | 111 | 0111 | ||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | 10 | 1000 | 1000 | ||||||||||||||||||||||||||||||||||||||||
| 9 | 9 | 11 | 1001 | 1001 | ||||||||||||||||||||||||||||||||||||||||
| 10 | А | 12 | 1010 | 00010000 | ||||||||||||||||||||||||||||||||||||||||
| 11 | В | 13 | 1011 | 00010001 | ||||||||||||||||||||||||||||||||||||||||
| 12 | С | 14 | 1100 | 00010010 | ||||||||||||||||||||||||||||||||||||||||
| 13 | D | 15 | 1101 | 00010011 | ||||||||||||||||||||||||||||||||||||||||
| 14 | Е | 16 | 1110 | 00010100 | ||||||||||||||||||||||||||||||||||||||||
| 15 | F | 17 | 1111 | 00010101 | ||||||||||||||||||||||||||||||||||||||||
| 16 | 10 | 20 | 10000 | 00010110 | ||||||||||||||||||||||||||||||||||||||||
| - | - | - | - | - | ||||||||||||||||||||||||||||||||||||||||
| 59 | 3B | 73 | 111011 | 01011001 | ||||||||||||||||||||||||||||||||||||||||
Введение.
Принцип представления чисел в позиционных системах счисления.
|
| Поделиться: |

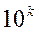 , где k – целое число. Например, число 125,46 можно представить в виде суммы:
, где k – целое число. Например, число 125,46 можно представить в виде суммы: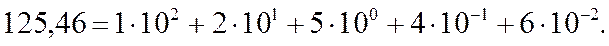
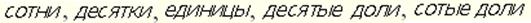
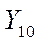 в десятичной системе счисления можно представить в виде подобной суммы: (Слайд).
в десятичной системе счисления можно представить в виде подобной суммы: (Слайд).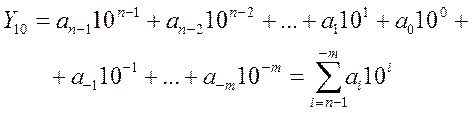 (1.1)
(1.1)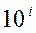 – вес i-го разряда;
– вес i-го разряда;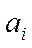 – весовой коэффициент для i-го разряда числа.
– весовой коэффициент для i-го разряда числа.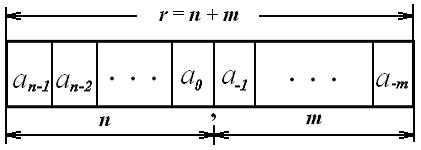
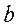 выражение (1.1) преобразуется к виду:
выражение (1.1) преобразуется к виду: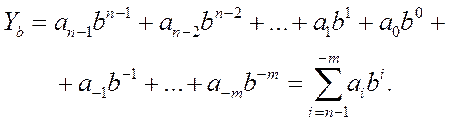 (1.2)
(1.2)
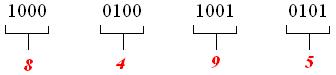
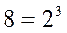 , а основание шестнадцатеричной системы – это
, а основание шестнадцатеричной системы – это 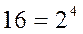 . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.
. Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.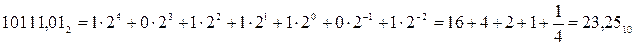
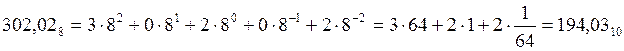
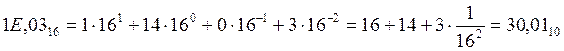
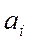 используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 1.2. Для нашего примера вместо знака "
используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 1.2. Для нашего примера вместо знака " 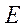 " в расчетную формулу (1.2) подставляется десятичное число
" в расчетную формулу (1.2) подставляется десятичное число 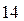 .
.


