
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гаусса в электростатике.Содержание книги Поиск на нашем сайте
Теорема Гаусса в интегральном виде. Если заряд распределён внутри поверхности, то
Металлы в электростатике. В металлах есть свободные электрические заряды; в диэлектриках все электрические заряды связаны между собой. Внутри металла всегда Е = 0 в результате поляризации (заряды выстраиваются в определённом порядке).
Задача: Задача: дана сфера:
Задача: даны 3 сферы.
Задача: найти
Задача: найти
Задача: найти
Конденсатор. Плоский: вне конденсатора электрическое поле равно нулю (компенсируется двумя пластинами). Внутри конденсатора:
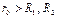 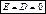 . . При  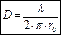 , , 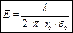
Работа электрического поля. Потенциал.
Физический смысл разности потенциалов – равен работе по перемещению единичного электрического заряда между двумя положениями.
Потенциал – энергетическая характеристика электрического поля. При
Потенциал точечного заряда.
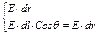 . .
Если имеется заряженное тело, то
Если заряды распределены по поверхности, то Если заряды распределены по линии, то Если перемещение равно 0, то есть по замкнутому контуру, то Если в поле работа не зависит от формы пути, то это поле потенциальное. Если а поле циркуляция по любому контуру равна 0, то поле безвихревое.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 51; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.009 с.) |

 – поле. S – замкнутая поверхность.
– поле. S – замкнутая поверхность. 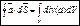 – полный поток векторного поля через любую замкнутую поверхность. Например:
– полный поток векторного поля через любую замкнутую поверхность. Например: 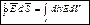 .
.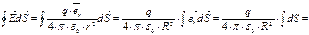
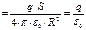 .
.  – полный поток
– полный поток 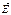 через сферическую поверхность.
через сферическую поверхность.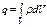 , и
, и  .
. 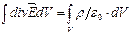 .
.  – теорема Гаусса в дифференциальном виде.
– теорема Гаусса в дифференциальном виде. =>
=>  .
.  – теорема Гаусса для индукции, где
– теорема Гаусса для индукции, где 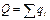 .
. 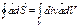 ;
; 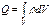 ;
; 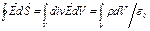 .
.
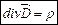 – теорема Гаусса для индукции в дифференциальном виде.
– теорема Гаусса для индукции в дифференциальном виде.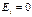 – тангенциальная составляющая на поверхности металла; так как заряд не двигается.
– тангенциальная составляющая на поверхности металла; так как заряд не двигается. –площадь поперечного сечения цилиндра,
–площадь поперечного сечения цилиндра, 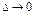 .
.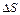 – площадь цилиндра.
– площадь цилиндра. ;
; 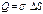 ;
; 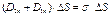 ;
;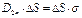 ;
; 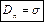 ,
, 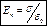 .
. 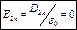 .
. 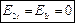 .
.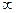 заряженная плоскость. Найти
заряженная плоскость. Найти  и
и  в т. А. Возьмём цилиндр и точка А будет лежать на основании этого цилиндра. S – площадь основания цилиндра.
в т. А. Возьмём цилиндр и точка А будет лежать на основании этого цилиндра. S – площадь основания цилиндра. 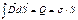 . Для боковой поверхности цилиндра
. Для боковой поверхности цилиндра 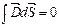 , так как
, так как  ,
, 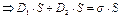
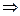
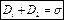 , но из-за симметрии
, но из-за симметрии 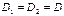 , и поэтому
, и поэтому 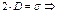
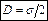 – для любой точки независимо от расстояния от плоскости.
– для любой точки независимо от расстояния от плоскости. 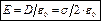 .
. ,
,  и
и  – полный заряд. Найти
– полный заряд. Найти 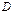 и
и 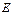 в произвольной точке на расстоянии
в произвольной точке на расстоянии  от центра сферы.
от центра сферы.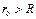 :
: 
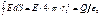 .
.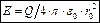 ,
, 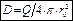 – сфера действует как точечный заряд.
– сфера действует как точечный заряд.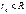 :
: 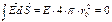
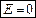 – внутри заряженной сферы.
– внутри заряженной сферы.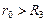 :
:  ;
;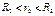 :
:  ;
;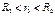 :
: 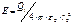 ;
; :
: 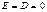 .
. заряженной нити на расстоянии
заряженной нити на расстоянии 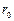 . Строим цилиндр и точка А будет находится на его боковой стороне.
. Строим цилиндр и точка А будет находится на его боковой стороне. 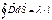 . Индукция и напряжённость остаются только от боковой стороны, так как на основаниях они
. Индукция и напряжённость остаются только от боковой стороны, так как на основаниях они 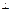 .
. ;
; 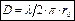 ,
, 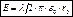 .
.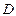 и
и  и
и  .
.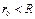 :
: 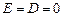 – внутри цилиндра поля нет;
– внутри цилиндра поля нет;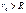 :
: 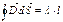 ;
; 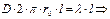
 ,
, 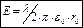 – как для
– как для 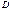 и
и 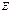 на расстоянии
на расстоянии 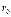 от заряженного шара:
от заряженного шара: 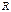 ,
,  .
. :
: 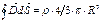 ,
, 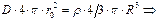
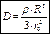 ,
,  .
.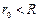 :
: 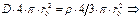
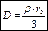 ,
, 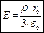 .
.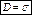 ,
, 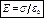 .
.
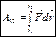 ,
, 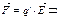
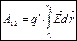 .
.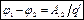 – разность потенциалов.
– разность потенциалов.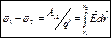 . Обычно принимает, что на
. Обычно принимает, что на 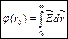 .
.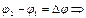
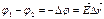 .
. 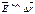 :
: 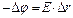
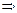
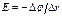
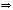 и при
и при 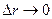 будет
будет  .
. 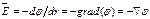 .
. 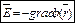 .
.
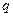
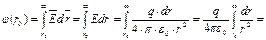
 .
. 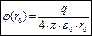 .
. 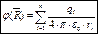 .
.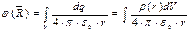 .
. .
.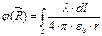 .
. – циркуляция вектора напряжённости по замкнутому контуру равна нулю.
– циркуляция вектора напряжённости по замкнутому контуру равна нулю.


