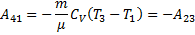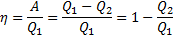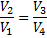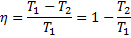Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Газові закони. Закон авагадро. Закон дальтона.Содержание книги Поиск на нашем сайте
Гази не зберігають ні форми, ні об’єму. — Характер молекулярного руху в газах — безладний (хаотичний) рух. Газові закони визначають кількісну залежність між двома параметрами даної маси газу при фіксованому значенні третього параметру. Процеси, перебіг яких відбувається при незмінному значенні одного із параметрів, називаються ізопроцесами.
Закон Авогадро: моли будь-яких газів при нормальних умовах (Т = 273 К, р = 1,01·105 Па) займають однаковий об'єм рівний 22,41·10-3 м3/моль. Закон Дальтона: тиск суміші газів дорівнює сумі парціальних тисків складових газів: Парціальний тиск — це тиск, який створював би газ, якби він займав даний об’єм сам.
Робота ідеального газу.
У розріджених газів молекули практично не взаємодіють між собою. Вони лише іноді стикаються один з одним. Однак ці зіткнення відбуваються настільки рідко, що більшу частину часу молекули рухаються вільно. Ідеальним називають такий газ, для якого можна знехтувати розмірами молекул та силами молекулярної взаємодії.
pV = b, b – константа пропорціональна масі тіла T Реальні гази поводять себе як ідеальний тоді, коли середня відстань між молекулами у багато разів перевищує їхні розміри, тобто коли розрідження досить велике. Газ може бути в різних станах, тобто деяка маса газу має об’єм V, тиск p і температуру Т. Величини V, p,Т, що характеризують стан газу, називаються термодинамічними параметрами.
Умови, за яких реальні гази можна вважати ідеальними
39Теплота. Внутрішня енергія. Перший принцип термодинаміки.
Внутрiшня енергiя - однозначна функцiя термодинамiчного стану системи, тобто в кожному станi система володiє цiлком певною внутрiшньою енергiєю (вона не залежить вiд того, як система прийшла в даний стан). Це означає, що пiд час переходу системи з одного стану в iнший зміна внутрiшньої енергiї визначається тiльки рiзницею значень внутрiшньої енергiї цих станiв i не залежить вiд шляху переходу. Перший закон термодинамiки: теплота, що надається системi, витрачається на змiну її внутрiшньої енергiї i на здiйснення нею роботи проти зовнiшнiх сил. Q = ∆U + A
або в бiльш коректнiй формi δQ = dU + δA
де dU - нескiнченно мала змiна внутрiшньої енергiї системи δA елементарна робота δQ - нескiнченно мала кiлькiсть теплоти. В цьому виразi dU є повним диференцiалом δA а δQ такими не є. 40. Теплоємність 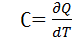 Теплоємність при сталому об’ємі Теплоємність при сталому об’ємі 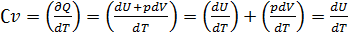 Теплоємність при сталому тиску Теплоємність при сталому тиску 
Співвідношення Маєра
41.Внутрішня енергія ідеального газу: 42.Закон Больцмана: -розподіл однакових частинок, що складають макросистему поліпотенціальних сил -ідеальний газ в полі потенціальній системі
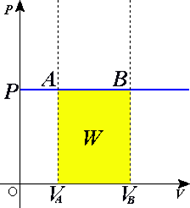
43) Процеси в ідеальному газі 1. P=const При ізобаричному процесі об'єм ідеального газу прямопропорційний температурі (див. Закон Гей-Люссака). На графіках процес зображується лініями, які називаються ізобарами. Для ідеального газу вони є прямими у всіх діаграмах, які пов'язують параметри T (температура), V (об'єм) і P (тиск).
Жовта ділянка відповідає роботі газу. З визначення роботи слідує, що макроскопічна робота при нескінченно малій зміні об'єму на величину dV при ізобаричному процесі дорівнює:
Повна робота процесу визначається інтегралом від даного виразу:
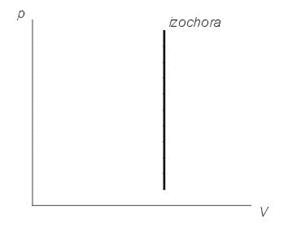
2. V=сonst При ізохоричному процесі тиск ідеального газу прямопропорційний його температурі. Закон Шарля:
На графіках зображується лініями, які називаються ізохорами. Для ідеального газу вони є прямими у всіх діаграмах, які пов'язують параметри T (температура), V (об'єм) і p (тиск). З визначення роботи слідує, що зміна роботи при ізохоричному процесі дорівнює:
Щоб визначити повну роботу процесу проінтегруємо даний вираз. Оскільки об'єм сталий, то:
Але такий інтеграл дорівнює нулю. Отже, при ізохоричному процесі газ роботи не виконує:
3. T=const
Якщо до ізотермічного процесу застосувати рівняння Клапейрона, то з урахуванням сталості температури
або
Робота при ізотермічному процесі:
Таким чином, робота, яка виконується ідеальним газом при ізотермічному процесі, визначається формулою
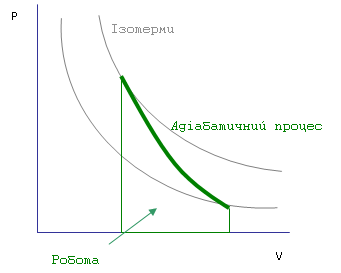
4. Q=0 (Адіабатичний процес)
При адіабатичному розширенні внутрішня енергіяробочого тіла повинна зменшуватись Роботу, яка виконується газом при адіабатичному процесі, можна знайти декількома способами. У першому способі можна за допомогою рівняння адіабати знайти залежність тиску від об’єму (
або
Підставивши вираз для внутрішньої енергії
Напишемо цю формулу у вигляді
Використаємо рівняння Пуассона для адіабатичного процесу
З рівняння стану випливає, що
Математично адіабатичний процес описується рівнянням
де p — тиск, V — об'єм,
Для адіабатичного процесу теплообмін з навколишнім середовищем відсутній, тобто кількість теплоти
де E — внутрішня енергія системи, а W — робота, що виконується самою системою. Будь-яка робота (W) здійснюється за рахунок витрат внутрішньої енергії E, адже надходження теплоти ззовні немає. Робота W, що виконується системою визначається як
Однак p не залишається константою в адіабатичному процесі, а змінюється разом з V. Бажано знати, як величини
де R — універсальна газова стала. Нехай задані
Тепер підставимо (2) та (3) в рівняння (1) та отримаємо:
спрощуючи,
Розділимо обидві частини на pV,
З диференціального числення відомо, що
що може бути записано як
для визначених констант
Після зведення у ступінь обох частин,
та позбавлення від мінуса,
тоді
та
44) Ентропія ідеального газу У кінцевому оборотному процесі зміни ентропії може бути підраховане по формулі:
1. P=const Оскільки у системі при ізобаричному процесі відбувається теплообмін із зовнішнім середовищем, то відбувається зміна ентропії. З визначення ентропії випливає:
Вище вже було виведено формулу для визначення кількості теплоти. Перепишемо її у диференціальному вигляді:
де ν — кількість речовини,
Або, якщо проінтегруємо останній вираз, повна зміна ентропії після проходження процесу:
У цьому випадку виносити вираз молярної теплоємності при сталому тиску за знак інтегралу не можна, оскільки вона є функцією, яка залежить від температури. 2. V=const Оскільки у системі при ізохоричному процесі відбувається теплообмін із зовнішнім середовищем, то відбувається зміна ентропії. З визначення ентропії випливає:
Вище вже було виведено формулу для визначення кількості теплоти. Перепишемо її у диференціальному вигляді:
де ν — кількість речовини,
Або, якщо проінтегруємо останній вираз, повна зміна ентропії після проходження процесу:
У цьому випадку виносити вираз молярної теплоємності при сталому об'ємі за знак інтегралу не можна, оскільки вона є функцією, яка залежить від температури. 3. T=const T 1 = T 2:
4. Q=0 (Адіабатний) При адіабатному процесі dQ=0, а отже ентропія S=0.
45) Циклічні процеси. Теплова машина. Коефіцієнт корисної дії теплової машини
З формулювання другого початку т/д по Кельвіну випливає, що вічний двигун другого роду неможливий. (Вічний двигун – це періодично діючий двигун, що робить роботу за рахунок охолодження одного джерела теплоти.)
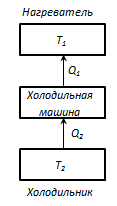
Термостат – це т/д система, яка може обмінюватися теплотою з тілами без зміни температури. Принцип дії теплового двигуна: від термостата з температурою Т 1 - нагрівача, за цикл віднімається кількість теплоти Q 1, а термостату з температурою Т 2 (Т 2 < Т 1) -холодильнику, за цикл передається кількість теплоти Q 2, при цьому відбувається робота А = Q 1 - Q 2
Круговим процесом або циклом називається процес, при якому система, пройшовши через ряд станів, вертається у вихідне. На діаграмі станів цикл зображується замкненою кривою. Цикл, чинений ідеальним газом, можна розбити на процеси розширення (1-2) і стиску (2-1), робота розширення позитивна А 1-2 > 0, тому що V 2 > V 1, робота стиску негативна А 1-2 < 0, тому що V 2 < V 1. Отже, робота чинена газом за цикл, визначається площею, охоплюваної замкненою кривою 1-2-1. Якщо за цикл відбувається позитивна робота зворотний цикл (цикл відбувається в напрямку проти годинникової стрілки). Прямий цикл використовується в теплових двигунах - періодично діючих двигунах, що роблять роботу за рахунок отриманої ззовні теплоти. Зворотний цикл використовується в холодильних машинах - періодично діючих установках, у яких за рахунок роботи зовнішніх сил теплота переноситься до тіла з більш високою температурою. У результаті кругового процесу система вертається у вихідний стан і, отже, повна зміна внутрішньої енергії дорівнює нулю. Тоді I початок т/д для кругового процесу Q = ΔU + A = A, т. т. робота, чинена за цикл дорівнює кількості отриманої ззовні теплоти, але Q = Q 1 - Q 2 Q 1 - кількість теплоти, отримана системою, Q 2 - кількість теплоти, віддана системою. Термічний к.к.д. для кругового процесу дорівнює відношенню роботи, зробленою системою, до кількості теплоти, підведеною до системи:
Щоб η = 1, повинне виконуватися умова Q 2 = 0, тобто тепловий двигун повинен мати одне джерело теплоти Q 1, але це суперечить другому початку т/д. Процес зворотний, що відбувається в тепловому двигуні, використовується в холодильній машині.
Від термостата з температурою Т 2 віднімається кількість теплоти Q 2 і передається термостату з температурою T 1, кількість теплоти Q 1. Q = Q 2 - Q 1 < 0, отже A < 0. Без здійснення роботи не можна відбирати теплоту від менш нагрітого тіла й віддавати її більш нагрітому.
Ґрунтуючись на другому початку т/д, Карно вивів теорему. Теорема Карно: із усіх періодично діючих теплових машин, що мають однакові температури нагрівачів (Т 1) і холодильників (Т 2), найбільшим к.к.д. мають оборотні машини. К.К.Д. оборотних машин при рівних Т 1 і Т 2 рівні й не залежать від природи робочого тіла. Робоче тіло – тіло, що робить круговий процес, що й обмінюються енергією з іншими тілами. Цикл Карно – оборотний найбільш економічний цикл, що полягає з 2-х ізотерм і 2-х адіабат.
2-3 – адіабатичне розширення, газ робить роботу A 2-3>0 над зовнішніми тілами. 3-4-ізотермічний стиск при Т 2 холодильника; відбирається теплота Q 2 і відбувається робота;
4-1-адіабатичний стиск, над газом відбувається робота A4-1<0 зовнішніми тілами. При ізотермічному процесі U = const, тому Q 1 = A 12
При адіабатичному розширенні Q 2-3 = 0, і робота газу A 23 відбувається за рахунок внутрішньої енергії A23 = - U
Кількість теплоти Q 2, віддана газом холодильнику при ізотермічному стиску дорівнює роботі стиску А 3-4
Робота адіабатичного стиску
Робота, чинена в результаті кругового процесу A = A 12 + A 23 + A 34 + A 41 = Q 1 + A 23 - Q 2 - A 23 = Q 1 - Q 2 і дорівнює площі кривій 1-2-3-4-1. Термічний к.к.д. циклу Карно
З рівняння адіабати для процесів 2-3 і 3-4 одержимо
Тоді
т.т. к.к.д. циклу Карно визначається тільки температурами нагрівача й холодильника. Для збільшення к.к.д. потрібно збільшувати різницю Т 1 - Т 2. 46. Цикл Карно. ККД теплової машини, що працює за циклом Карно Цикл Карно – теплова машина, що має 2 теплових резервуари(2 тіла, які підтримують сталу Т), складається з 2 ізотермічних та 2 адіабатичних процесів.
ККД для циклу Карно
47. Принцип Кельвіна. Перша теорема Карно Принцип Кельвіна: не може існувати процес, у якому машина виконує роботу та обмінюється енергією лише з одним тепловим резервуаром. Перша теорема Карно: якщо є теплові машини, які працюють за зворотнім циклом Карно, а температури холодильника і нагрівача однакові та ККД однакові. 48. Друга теорема Карно ККД теплової машини, яка працює за незворотнім циклом Карно, не може бути більше за ККД машини, що працює за зворотнім циклом Карно при умові рівності температур нагрівача і холодильника.
49.Неравенство Клаузиуса Для получения неравенства Клаузиуса в общем виде можно рассмотреть систему A, работающую с n резервуарами температур Ti и получающую от них тепло Qi. Вводится дополнительный Резервуар температуры T0. Между ним и остальными резервуарами запускаются машины Карно — по одной на каждый.
Циклы Карно проводятся таким образом, чтобы передавать резервуарам столько тепла, сколько они передали системе А. Тогда. Это тепло отдаст резурвуар температуры T0, в то время как состояние остальных резервуаров вернётся к исходному. Следовательно, рассмотренный процесс эквивалентен процессу передачи тепла резурвуаром температуры T0 системе A, причём совокупность «система A — резервуар T0» теплоизолирована. Следовательно, по первому началу термодинамики системой A совершена работа. В соответствии с формулировкой Томсона второго начала термодинамики эта работа не может быть положительной. Отсюда очевидно неравенство Клаузиуса в общем виде:
2.Приведенная теплота - отношение теплоты Q в изотермическом процессе к температуре, при которой происходила передача тепллоты Q'=Q/T
50. Термодинамическая энтропия Термодинамическая энтропия S, часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).
Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Поэтому для простых равновесных систем существует функция состояния , полный дифференциал которой равен (Дефиниция энтропии простой равновесной системы) где Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель T есть абсолютная термодинамическая температура.Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.
50. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов, которые могут происходить в термодинамических системах. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).
Второе начало термодинамики является постулатом, не доказываемым в рамках классической термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Другая формулировка второго начала термодинамики основывается на понятии энтропии: «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии). Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.
51.Распределение Максвела Рассмотрим пространство скоростных точек (каждую скорость молекулы представляем как точку (скоростную точку) в системе координат) в стационарном состоянии газа. Выберем бесконечно малый элемент объема. Так как газ стационарный, количество скоростных точек в остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функции плотности вероятности для всех направлений одинаковы.
Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента Vх скорости молекулы не зависит от y- и z- компонент. - фактически вероятность нахождения скоростной точки в объеме Правая часть не зависит от Vy и Vz, значит и левая от Vy и Vz не зависит. Однако Vx и Vy равноправны, следовательно левая часть не зависит также и от Vx. Значит данное выражение может лишь равняться некоторой константе. Теперь нужно сделать принципиальный шаг — ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул): Ввиду равноправия всех направлений:
Чтобы найти среднее значение Vx^2, проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:
Отсюда найдём a:
Функция распределения плотности вероятности для Vx (для Vy и Vz аналогично):
Теперь рассмотрим распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скороcти лежат в шаровом слое радиуса V и толщины , и - объем этого шарового слоя.
Таким образом, мы получили функцию плотности вероятности F(v), которая и является распределением Максвелла.
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.188 (0.011 с.) |



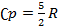
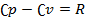
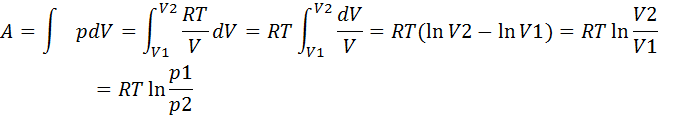


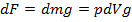

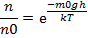

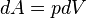
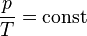 ,
,
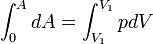 ,
,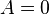 .
.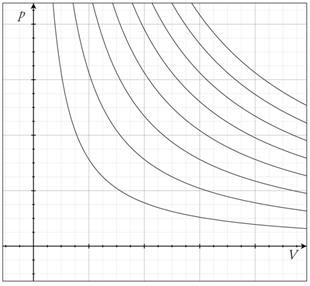
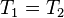 воно набуде вигляду
воно набуде вигляду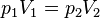
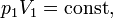
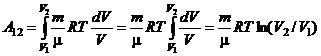 .
.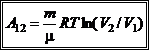
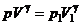 ,
, 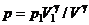 ), підставити цю залежність і знайти шукану роботу
), підставити цю залежність і знайти шукану роботу 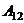 . У другому способі використаємо перший закон термодинаміки, візьмемо до уваги, що для адіабатичного процесу
. У другому способі використаємо перший закон термодинаміки, візьмемо до уваги, що для адіабатичного процесу 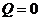 . Тоді
. Тоді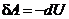
 .
.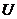 в цю формулу, знаходимо роботу ідеального газу при адіабатичному процесі
в цю формулу, знаходимо роботу ідеального газу при адіабатичному процесі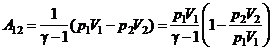 .
. .
.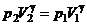 . Тоді остаточно
. Тоді остаточно .
.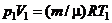 . Зробивши таку заміну, отримаємо ще один вираз для роботи, яка виконується ідеальним газом при адіабатичному процесі:
. Зробивши таку заміну, отримаємо ще один вираз для роботи, яка виконується ідеальним газом при адіабатичному процесі:
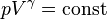
 — показник адіабати,
— показник адіабати,
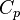 — молярна теплоємність за умов постійного тиску, а
— молярна теплоємність за умов постійного тиску, а 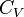 — молярна теплоємність за умов постійного об'єму. Для одноатомного ідеального газу,
— молярна теплоємність за умов постійного об'єму. Для одноатомного ідеального газу, 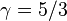 , а для двоатомного (таких як азот або кисень, головних складовихповітря)
, а для двоатомного (таких як азот або кисень, головних складовихповітря) 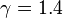 . Ця формула може бути застосована лише для класичних газів.
. Ця формула може бути застосована лише для класичних газів.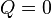 . Тоді, відповідно до першого закону термодинаміки,
. Тоді, відповідно до першого закону термодинаміки,

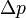 та
та 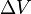 співвідносяться між собою в адіабатичному процесі. Припустимо тепер, що в нас є одноатомний газ, тоді
співвідносяться між собою в адіабатичному процесі. Припустимо тепер, що в нас є одноатомний газ, тоді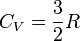
 та
та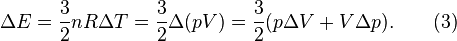


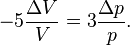
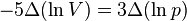
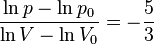
 та
та  первісного стану. Далі
первісного стану. Далі
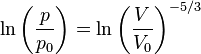
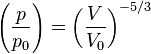
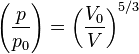
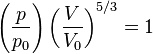

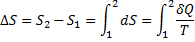
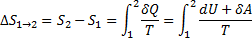



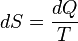
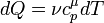 ,
, — молярна теплоємність при сталому тиску. Отже, мікроскопічна зміна ентропії при ізобаричному процесі може бути визначена за формулою:
— молярна теплоємність при сталому тиску. Отже, мікроскопічна зміна ентропії при ізобаричному процесі може бути визначена за формулою:

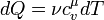 ,
,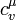 — молярна теплоємність при сталому об'ємі. Отже, мікроскопічна зміна ентропії при ізохоричному процесі може бути визначена за формулою:
— молярна теплоємність при сталому об'ємі. Отже, мікроскопічна зміна ентропії при ізохоричному процесі може бути визначена за формулою:
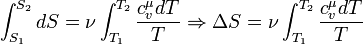
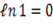


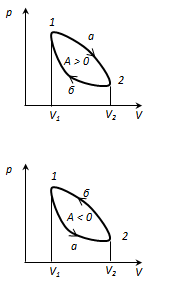
 (цикл за годинниковою стрілкою), то цикл називається прямим, якщо
(цикл за годинниковою стрілкою), то цикл називається прямим, якщо  -
-
 1 - 2-ізотермічне розширення при Т 1 нагрівача; до газу підводить теплота Q 1 і відбувається робота
1 - 2-ізотермічне розширення при Т 1 нагрівача; до газу підводить теплота Q 1 і відбувається робота 
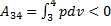 ;
;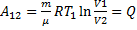 1
1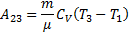
 2
2