
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведене рівняння Ван-дер-ВаальцаСодержание книги Поиск на нашем сайте
δP/δVM=-RT/(VM-b)2+2a/V3M=0 δ2P/δV2M=2RT/(VM-b)3-6a/V4M=0 Vкр=3b, φ=VM/VМ кр Pкр=а/27b2, π=P/Pкр Tкр=8а/27bR, τ=T/Tкр (πPкр+a/φ2V2M кр)(φVМ кр-b)=RτTкр (πa/27b3+a/φ29b2)(3φb-b)=Rτ8a/27bR (π+3/φ2)(φ-1/3)=8τ/3
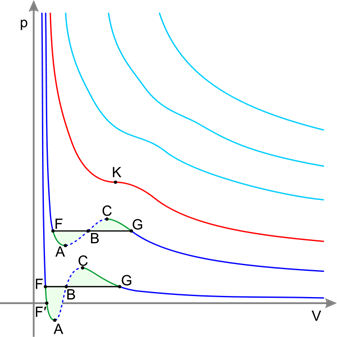
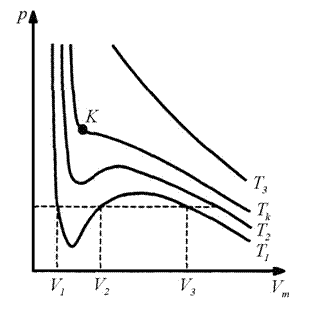
64. Ізотерма реального газу -ізотерма, що описує залежність між тиском та об'ємом реального газу при постійній температурі за допомогою рівняння ван дер Ваальса. Оскільки весь процес відбувається при сталій температурі Т, криву, що зображує залежність тиску р від об'єму V, називають ізотермою. Для дослідження поведінки одного моля реального газу розглянемо ізотерми Ван-дер-Ваальса, які визначаються рівнянням: Перетворимо це рівняння у вигляд: і
Ізотерми газу, які описуються рівнянням Ван-дер-Ваальса, мають вигляд, де
Для кожної речовини існує свій критичний стан, який визначається критичною температурою, тиском і об’ємом. Теоретично розрахувати критичні параметри газу можна розв’язавши рівняння Ван-дер-Ваальса. Це рівняння третього степеня відносно об’єму. Одному значенню тиску відповідає три значення об’єму. При критичному значенні температури всі три корені будуть рівні між собою. Розв’язавши рівняння для цього випадку, визначають критичні параметри газу, взятого у кількості 1 моля:
Критична температура речовини дорівнює тій температурі при якій густина рідини і густина її насиченої пари стають однаковими. Критичний тиск дорівнює максимальному значенню тиску, який може мати насичена пара даної речовини. Критичний об’єм є максимальним об’ємом, який може займати речовина у рідкому стані при критичній температурі і тискові. Співвідношення між критичними параметрами газу набуває вигляду
Якщо газ охолоджувати при критичної щільності, то він при температурі приблизно на один градус вище критичної починає випромінювати блакитне світло опалесценції, інтенсивність якого сильно збільшується з наближенням до критичної точки, хоча система все ще залишається гомогенної. Це явище засноване на тому, що при наближенні до критичної точки сильно зростає насамперед у прямому напрямку інтенсивність розсіювання світла. Такі ж явища спостерігаються в критичній точці розшарування рідких і твердих систем. В останньому випадку для доказу потрібно, звичайно, використовувати рентгенівські промені. Критична опалесценція є, як показує теоретичний аналіз, безпосереднім наслідком того факту, що критична точка розташована на кордоні області стабільності. Відомо, що поблизу критичної точки абсолютно прозора середу стає мутной- відбувається інтенсивне розсіювання світла, причому в безпосередній близькості від критичної точки інтенсивність розсіяного світла / Це явище носить назву критичної опалесценції. 65. Фа́зовий перехі́д у фізиці означає таку трансформацію внутрішньої структури речовин, при якій відбувається різкий стрибок певної фізичної характеристики системи, викликаний малою зміною іншої характеристики. Розрізняють фазові переходи першого і другого роду. При фазових переходах першого роду поглинається або виділяється прихована теплота. Фазові переходи другого роду відбуваються без поглинання чи виділення тепла. Така сучасна класифікація дещо відрізняється від класифікації Еренфеста, який назвав фазовими переходами першого роду переходи, при яких стрибком міняються перші похідні від вільної енергії, а фазовими переходами другого роду ті, при яких стрибком міняються, відповідно другі похідні від вільної енергії. Інші, відмінні від вільної енергії термодинамічні потенціали, наприклад, внутрішня енергія або ентальпія при фазових переходах першого роду міняються стрибком. Недоліком класифікації Еренфеста є те, що при деяких фазових переходах похідні від вільної енергії прямують до нескінченності, наприклад теплоємність при фазовому переході до феромагнітного стану. Фазові переходи розділяють на дві категорії: при фазових переходах першого роду значення термодинамічних потенціалів змінюються стрибком, при фазових переходах другого роду стрибком змінюються похідні від термодинамічних потенціалів, а самі термодинамічні потенціали залишаються неперервними функціями своїх аргументів. Правило фаз визначає можливість співіснування різних агрегатних станів речовин. Для однокомпонентної речовини водночас може існувати максимум три фази — таке відбувається в потрійній точці. Для багатокомпонентних речовин, наприклад сплавів, одночасно може існувати більше фаз. Криві співіснування фаз задаються фазовими діаграмами. Прикладами фазових переходів є: · зміна агрегатного стану (випаровування, сублімація і т.п.) · перехід речовини до стану надплинності · перехід до надпровідності · перехід між феромагнетиком і парамагнетиком, сегнетоелектриком і діелектриком. · перехід між рідкокристалічною фазою і фазою звичайної ізотропної рідини.
66. Співвідно́шення Кла́узіуса — Клапейро́на — рівняння, яке задає закон залежності тиску від температури на кривій співіснування фаз.
де P — тиск, T — температура, Q — прихована теплота, Формула Клаузіуса — Клапейрона є наслідком рівності хімічних потенціалів різних фаз при фазовому переході. У випадку рівноваги між твердим тілом і газом, об'ємом твердого тіла можна знехтувати, а для газу застосувати рівняння Менделеєва-Клапейрона. Тоді співвідношення зводиться до форми
де R — газова стала. Рудольф Клаузіус вивів його із законів термодинаміки.
67. Приклади фазових переходів 1 роду. Фазова діаграма Найбільш поширені приклади фазових переходів першого роду: Фазова діаграма — графічне зображення ліній співіснування фаз у залежності від термодинамічних параметрів. 68. Приклади фазових переходів 2 роду. Рідкий гелій. Явище надплинності Найбільш поширені приклади фазових переходів другого роду: Надплинність — стан речовини, в якому вона втрачає в'язкість
|
|||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.8.126 (0.01 с.) |

 .
.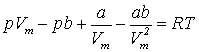
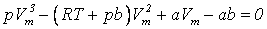 .
. .
.
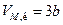 ,
, 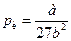 ,
,  .
.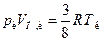 . У критичній точці
. У критичній точці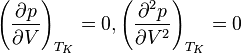
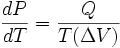 ,
,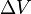 — зміна об'єму речовини при фазовому переході.
— зміна об'єму речовини при фазовому переході.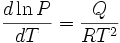 ,
,


