Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Й закон Ньютона в неірцеальній системі відлікуСодержание книги Поиск на нашем сайте
НеІСВ- системи, які рух. Одна відносно одної з прискоренням(поступ. Оберт.)
27) Є 2 постулати Ейнштейна: Принцип відносності, принцип інваріантності швид. світла
28 Перетворення Лоренца Перетворення Лоренца для координат часу
Нехай у т. А відбувається певна подія. У "нерухомій" системі К вона характеризується значеннями координат і часу: У системі Перемножимо ці вирази, та отримаємо Це означає, що Аналогічно Координата точки О у системі K а у системі K' Ці два вирази повинні обертатися в нуль одночасно, тобто Припустимо, що вздовж осі Х посилається світловий сигнал, спалах від якого реєструється в кожній системі. При цьому оскільки швидкість світла в обох системах однакова: Виконавши низку перетворень та врахувавши, що Отримаємо Перетворення Лоренца
При швидкостях, набагато менших за швидкість світла, перетворення Лоренца не відрізняються від перетворень Галілея. 29 Наслідки з перетворень Лоренца Наслідки з перетворень Лоренца * Відносність поняття одночасності: події одночасні в одній системі виявляються неодночасними в іншій. * Скорочення довжин: довжина стержня, який рухається виявляється меншою за довжину стержня, який перебуває у стані спокою. * Власний час менший за час, визначений за годинником, який рухається відносно тіла. * релятивістський закон перетворення швидкостей:
30 Закон перетворення швидкостей Проведемо дослідження формул додавання швидкостей в СТВ у граничних випадках. Розглянемо випадок, коли
формули додавання швидкостей, за допомогою яких перетворюються швидкості в ньютонівській механіці. Таким чином, коли Розглянемо випадок, коли частинка рухається паралельно осям
Швидкості
Таким чином, формула додавання швидкостей узгоджується с другим постулатом СТВ.
31. Релятивіський імпульс
Імпульс є інваріантним при переході від однієї СВ до іншої. У релятивістському випадку маса втрачає зміст коефіцієнта пропорційності між прискоренням і силою. Більше того, напрямки сила та прискорення можуть не збігатися. Крім того, на відміну від ньютонівської механіки сила
32. Релятивіський вираз для енергії
Енергія спокою це: кінетична енергія руху складових системи відносно центру мас; потенціальна енергія взаємодії всіх складових між собою.
33. Термодинамічна система Термодинамічна система – це сукупність мікроскопічних тіл, які взаємодіють і обмінюються енергією між собою і навколишнім середовищем. Термодинамічні параметри – параметри стану – сукупність фізичних величин, що характеризують властивості і стан термодинамічної с-ми. Такими параметрами є Т, V, р. Стан системи, у якому вона може перебувати досить довго (параметри стану у часі є незмінними), називається термодинамічною рівновагою Розрізняють екстенсивні параметри стану, пропорційні масі системи, й інтенсивні параметри стану, не залежать від маси системи. До екстенсивних належать об'єм, внутрішня енергія, ентропія, ентальпія, Гіббса енергія, Гельмгольца енергія (вільна енергія), до інтенсивних — тиск, температура, концентрація, магнітна індукція та ін. Не всі параметри стану незалежні (тобто ПС взаємопов’язані), тому що рівноважний стан системи можна однозначно встановити, знайшовши певні значення обмеженої кількості параметрів системи.
34. Ідеальний газ – газ у якому молекули не взаємодіють між собобю. 1) Молекули одноатомні 2) Молекули- матеріальальні точки, які мають масу. А їхніми розмірами можна знехтувати 3) Єдиний тип взаємодії – пружнє зіткнення 4) Ідеальний газ рівномірно заповнює весь наданий йому об*єм (внутрішня енергія ідеального газу залежить тільки від температури) Тиск – імпульс, який передається від кожної молекули газу до стінок посудини.
Де, n –концентрація речовини Ек- середня кінетична енергія руху молекул кінетичного газу, яка припадає на 1 моль молекул.
35.Середня кінетична енергія молекул визначається за формулою
І – загальне число ступенів вільності молекули, K – стала Больцмана
36. Рівн́яння стáну ідеáльного гáзу — формула, що встановлює залежність між тиском, молярним об'ємом і абсолютною температурою класичного ідеального газу. У хімії рівняння записують зазвичай для одного моля газу, й воно має вигляд:
· · · ·
Оскільки
Якщо записати
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.78 (0.011 с.) |



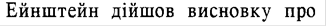


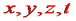
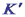 :
: 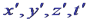
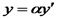 та
та 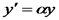
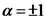
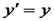 та
та 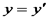
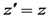 та
та 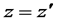


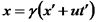
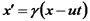
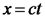
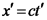
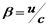
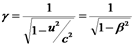

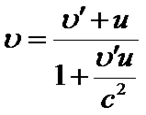
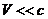 . У цій ситуації вираз
. У цій ситуації вираз 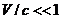 і ним можна в формулах (43.4)–(43.6) знехтувати. У результаті отримуємо, наприклад, з (43.4) та (43.5)
і ним можна в формулах (43.4)–(43.6) знехтувати. У результаті отримуємо, наприклад, з (43.4) та (43.5)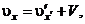
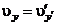 ,
, 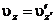
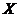 і
і 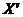 в напрямку швидкості
в напрямку швидкості 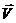 (див. рис. 42.1). Тоді
(див. рис. 42.1). Тоді  збігається з модулем швидкості частинки
збігається з модулем швидкості частинки 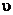 в системі
в системі 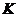 , a
, a 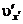 – з модулем швидкості
– з модулем швидкості 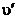 в системі
в системі  , і формула (43.4) має вигляд
, і формула (43.4) має вигляд . (43.7)
. (43.7)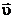 ,
, 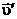 і
і 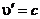 , то
, то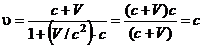 . (43.8)
. (43.8)
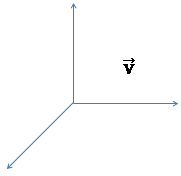
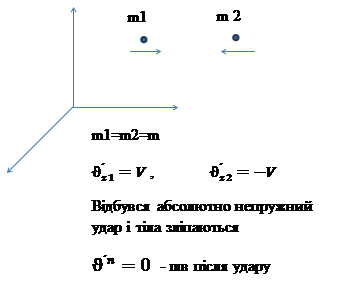
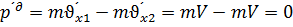
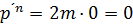
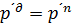

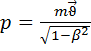 - релятивіський імпульс, закон збереження імпульсу(?)
- релятивіський імпульс, закон збереження імпульсу(?)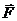 у релятивістській механіці не є інваріантною (у різних інерціальних системах відліку вона має різні модулі й напрямки).
у релятивістській механіці не є інваріантною (у різних інерціальних системах відліку вона має різні модулі й напрямки).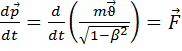

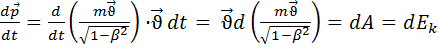
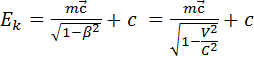
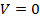 ,
, 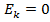 , тоді
, тоді 
 – вираз енергії кінетичної в релятивіській механіці
– вираз енергії кінетичної в релятивіській механіці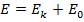 – повна енергія -закон збереження енергії(?)
– повна енергія -закон збереження енергії(?)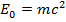 – енергія спокою(аналог внутрішньої енергії для молекул).
– енергія спокою(аналог внутрішньої енергії для молекул). - інваріант, величина однакова для всіх систем відліку.
- інваріант, величина однакова для всіх систем відліку.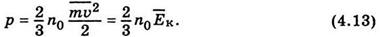
 де
де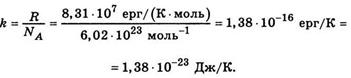
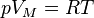 , де:
, де: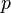 — тиск,
— тиск, — молярний об'єм,
— молярний об'єм,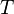 — абсолютна температура,
— абсолютна температура,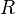 — універсальна газова стала.
— універсальна газова стала.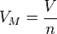 , де
, де 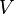 - повний об'єм газу, а
- повний об'єм газу, а 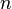 — кількість речовини, то рівняння можна записати у вигляді:
— кількість речовини, то рівняння можна записати у вигляді: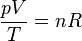
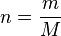 , де
, де 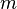 — повна маса газу,
— повна маса газу, 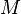 — молярна маса, рівняння стану виглядатиме так:
— молярна маса, рівняння стану виглядатиме так: