
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные виды фазовых траекторий линейных систем второго порядка.Содержание книги
Поиск на нашем сайте Уравнение системы второго порядка: Корни этого уравнения: Для разных значений a возможны шесть разных случаев, следовательно шесть фазовых траекторий. 1) корни чисто мнимые при a 1=0, а 2>0 (колебательная граница устойчивости линейной системы); получается незатухающие колебания (рис. 16.2, а)
Для фазовой плоскости уравнения представляют собой параметрические уравнения эллипса с полуосями А и ω A (рис. 16.2, б). Уравнение эллипса:
можно получить непосредственным решением дифференциального уравнения фазовых траекторий (16.3) при а1=0 и а2=ω2, причем A — произвольная постоянная интегрирования.
периодическим колебаниям системы (рис. 16.2, а) соответствует движение изображающей точки по замкнутой кривой(рис. 16.2, б). Фазовые траектории по замкнутой кривой 2) корни комплексные и имеют отрицательные вещественные части при это затухающие колебания (рис. 16.3, а)
Рис. 16.3
а произвольные постоянные A и β определяются из начальных условий:
Значения х и у не возвращаются за период колебания к прежним, а становятся меньше. Это дает на фазовой плоскости (х, у) кривую (рис. 16.3, б), которая за один оборот не возвращается в прежнюю точку М0, а подходит ближе к началу координат, то есть фазовые траектории в виде спиралей (рис. 16.3, б). 3) корни комплексные и имеют положительные вещественные части при Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траектории тоже в виде спиралей, но только изображающая точка будет двигаться по ним не к началу координат, а от него (рис. 16.4, б).
Рис. 16.4
4) корни вещественные отрицательные при апериодический процесс: где
Рис. 16.6 Здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка М не попадает в начало координат в конечное время, а приближается асимптотически. Фазовые траектории, вливающиеся в начало координат. (Рис. 16.6) 5) корни вещественные положительные при Этот случай (вещественные положительные корни) соответствует также апериодическому процессу, определяемому теми же уравнениями (16.5), но при α1<0 и α2<0. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 16.6.
Рис. 16.6 6) корни вещественные и имеют разные знаки при а 2<0 (неустойчивая линейная система); в частности, один из корней будет равен нулю при а 2 = 0 (апериодическая граница устойчивости линейной системы). Это апериодический процесс, но α1 и α2 имеют разные знаки, следовательно картина фазовых траекторий здесь иная. Так как а2<0, то α2= –а2, рассмотрим случай а1=0, что соответствует согласно (16.1) уравнению системы
и согласно (16.3) — уравнению фазовых траекторий
Интегрирование дает
т.е. семейство гипербол, изображенное на рис. 16.7, б.
рис. 16.7, б. Аналогичная картина фазовых траекторий получится в данном случае и при а1≠0. Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис. 16.6, б или типа рис. 16.7, б, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.
Основные понятия по Ляпунову об устойчивости нелинейных систем. Основные виды устойчивости нелинейных систем. Устойчивость по Ляпунову: «Невозмущенное движение устойчиво, если при достаточно малых начальных возмущениях вызванное ими возмущенное движение сколь угодно мало отличается от невозмущенного; при этом движение асимптотически устойчиво, если при t Невозмущенным движением системы - одно из возможных расчетных движений системы при некоторых определенных начальных условиях и заданном внешнем воздействии. Всякое другое движение называется возмущенным. Можно считать, что любое возмущенное движение получается за счет приложения к системе кратковременного внешнего возмущения при t = 0. От наличия внешних воздействий на систему, системы управления могут быть разделены на автономные и неавтономные. В автономных системах внешние воздействия отсутствуют. К автономной системе может быть сведена любая из непрерывных систем при не зависящем от времени внешнем воздействии. В неавтономных системах существуют зависящие от времени внешние воздействия. Так как в автономных нелинейных системах наиболее характерными: являются два процесса равновесие и автоколебания, то для них рассматриваются два различных понятия устойчивости: устойчивость равновесия и устойчивость автоколебаний. Для неавтономных систем существует понятие устойчивости процесса, обусловленного внешним воздействием. Состояние равновесия и установившийся режим автоколебаний можно рассматривать как важные частные случаи невозмущенных движений автономной системы. Для общего суждения об устойчивости движения пользуются понятием устойчивости, данным А. М. Ляпуновым: движение устойчиво, если для любой сколь угодно малой заданной области допустимых отклонений k от точки k = 0 можно указать область начальных значений лежащую внутри области и обладающую тем свойством, что ни одно возмущенное движение, начавшееся внутри области никогда не достигнет границы области .
Для характеристики устойчивости кроме областей и удобно ввести понятие области установившихся значений разности возмущенного и невозмущенного движений. При t
Вид области зависит от области начальных отклонений. Нужно отметить два практически важных частных случая областей . В первом случае = 0, т. е.
Такое движение называют асимптотически устойчивым. Если для выполнения равенства (18.4) требуется, чтобы область начальных отклонений была достаточно мала, то говорят об асимптотической устойчивости в малом. Если эта область может иметь конечные размеры, то говорят об асимптотической устойчивости в большом. Если, наконец, равенство (18.4) выполняется при сколь угодно больших начальных отклонениях, то говорят об асимптотической устойчивости в целом. Во втором частном случае область представляет собой отрезок на оси 1. В этом случае равенство (18.4) не выполняется при сколь угодно малых отклонениях от равновесия и устойчивость относится к неасимптотической. Для суждения об устойчивости автоколебаний вводится понятие орбитальной устойчивости. Периодическое движение (автоколебание) в пространстве состояний изображается некоторой замкнутой кривой Г. Представляя любую траекторию геометрическим местом конца вектора x (t), можно для любого момента времени t определить кратчайшее расстояние ох конца вектора x (t)до кривой Г, которое обозначим [ x (t), Г]. Под орбитально асимптотически устойчивым периодическим движением в автономной системе (автоколебанием) будем понимать такое движение, для которого
Это условие можно выразить с помощью понятия невозмущенного движения, если учесть возможный сдвиг по времени между x H (t) и х (t). Обозначив
можно условие орбитальной асимптотической устойчивости сформулировать следующим образом: существуют такие положительные вещественные значения = 0, для которых
Невыполнение условия (18.5) или (18.7) приводит к нарушению орбитальной асимптотической устойчивости.
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

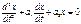
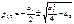
 (16.4)
(16.4)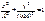

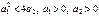 (устойчивая линейная система);
(устойчивая линейная система);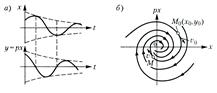
 где
где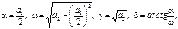
 .
. (неустойчивая линейная система);
(неустойчивая линейная система);
 (устойчивая линейная система);
(устойчивая линейная система); (16.5)
(16.5)

 (неустойчивая линейная система);
(неустойчивая линейная система);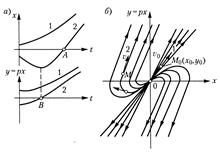
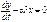
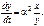 (16.6)
(16.6) ,
,
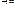 возмущенное движение стремится к невозмущенному.»
возмущенное движение стремится к невозмущенному.»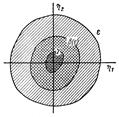 Области и на плоскости 1 и 2 схематически показаны на рис. 18.1
Области и на плоскости 1 и 2 схематически показаны на рис. 18.1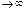
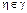 (18.3)
(18.3)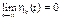 (18.4)
(18.4)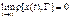 . (18.5)
. (18.5)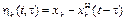 , (18.6)
, (18.6)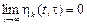 (18.7)
(18.7)


