
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез линейных систем по логарифмическим амплитудно-частотным характеристикам.Содержание книги
Поиск на нашем сайте
Пусть передаточная функция неизменяемой части системы
где Потребуем, чтобы система была астатической В некоторых случаях необходимо, чтобы при начальном рассогласовании Легко установить, что если порядок астатизма Задача сводится, следовательно, к синтезу корректирующего устройства, обеспечивающего необходимые динамические свойства системы. При этом будем полагать, что передаточная функция неизменяемой части системы
так как уже выяснено, какой передаточный коэффициент должен иметь усилительно-преобразовательный элемент и нужны ли в нем интегрирующие звенья. Метод синтеза корректирующих устройств, разработанный В. В. Солодовниковым, основывается на соответствии между логарифмическими частотными характеристиками разомкнутой системы и ее статическими и динамическими свойствами в замкнутом состоянии. Метод используется для систем минимально-фазового типа и поэтому достаточно рассматривать лишь логарифмическую амплитудно-частотную характеристику разомкнутой системы.
35. Основные понятия и определения по нелинейным системам. Нелинейные САУ – САУ, в которой хотя бы один элемент (звено) описывается нелинейными дифференциальными и/или алгебраическими уравнениями. Суть нелинейных систем заключается в том, что реакция системы на любую комбинацию внешних воздействий не равна сумме реакций на каждое из этих воздействий, поданных на систему порознь, то есть принцип суперпозиции не применим. Следовательно нет общей теории нелинейных дифференциальных уравнений, на основе которой могла бы быть создана общая теория нелинейных систем автоматического управления. Существует лишь ряд частных методов для решения некоторых видов нелинейных уравнений. Вместе с тем, если не ограничивать диапазон на изменения входных воздействий, то все реальные системы автоматического управления оказываются нелинейными. Трудность исследования нелинейных систем заставляет упрощать их описание. Желательным пределом такого упрощения является приближенное описание их линейными уравнениями, хотя бы в некоторых из интересующих нас режимов. Это называется линеаризацией нелинейных систем. Линеаризация – (от лат. linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной. Методы линеаризации имеют ограниченный характер, т. е. эквивалентность исходной нелинейной системы и её линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, либо для определенных процессов, причем, если система переходит с одного режима работы на другой, то следует изменить и её линеаризированную модель. Применяя линеаризацию, можно выяснить многие качественные и особенно количественные свойства нелинейной системы.
36. Нелинейные звенья систем управления. Основные характеристики типовых нелинейных звеньев. Нелинейные звенья систем управления. При рассмотрении различных нелинейных систем, в них встречаются нелинейности самого различного вида. Нелинейность всегда характеризуется соответствующей функцией z = z(x), где x – характеризует одномерную нелинейность.Возможны случаи и многомерных нелинейностей, когда переменная z — функция нескольких переменных. Примером двумерной нелинейности является звено, в котором скорость v движения поршня представляет собой функцию переменных γи у. Примерами многомерных нелинейностей могут служить у - показатель оптимальности, зависящей от нескольких переменных (х, f), устройство запоминания экстремума r (y, y)... Многомерные нелинейности можно так же представить соединением одномерных, что упрощает расчеты.
Характеристика типовых нелинейных звеньев. Звенья с однозначными непрерывными характеристиками. Такими характеристиками обладают некоторые схемы электронных, магнитных и гидравлических усилителей в области малых входных сигналов. Простейшей механической моделью зоны нечувствительности является система соединения двух валов с пружинным возвратом ведомого вала в нейтральное положение при наличии участка свободного хода (люфта) в системе передачи.
Звенья с однозначными разрывными характеристиками. Звено типа «двухпозиционное реле без гистерезиса». Однозначная характеристика двухпозиционного поляризованного реле показана на рис.14.4, а. При модуле входного сигнала Звенья с двузначными характеристиками.
Звено типа «люфт». Одна, из нелинейностей, наиболее часто встречающихся в механических системах, связана с наличием зазоров в системе передачи. Если в механической модели нелинейности типа «зона нечувствительности» (см. рис.14.2, д) убрать пружину, стремящуюся возвратить ведомый вал в нулевое положение, то получится модель нелинейности типа «люфт»
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.123.61 (0.008 с.) |

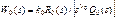 ,
,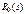 ;
; 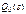 — полиномы от S со свободным членом, равным единице;
— полиномы от S со свободным членом, равным единице; 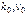 — постоянные величины.
— постоянные величины.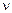 -го порядка, имела добротность
-го порядка, имела добротность 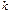 , перерегулирование не более
, перерегулирование не более 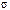 и время регулирования не более
и время регулирования не более 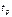 . Такой комплекс требований весьма часто предъявляют к следящим системам. Значения порядка астатизма
. Такой комплекс требований весьма часто предъявляют к следящим системам. Значения порядка астатизма 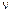 и добротности
и добротности 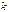 выбирают, исходя из необходимой точности регулирования в установившихся режимах. Выбором показателей качества переходной характеристики — перерегулирования
выбирают, исходя из необходимой точности регулирования в установившихся режимах. Выбором показателей качества переходной характеристики — перерегулирования 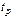 — гарантируются необходимые быстродействие и динамическая точность системы.
— гарантируются необходимые быстродействие и динамическая точность системы.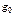 ускорение регулируемой координаты не превышало некоторого допустимого значения
ускорение регулируемой координаты не превышало некоторого допустимого значения 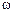 . Такое ограничение необходимо, например, в механических системах, когда регулируемой координатой является перемещение. Предупреждается появление в регулируемом объекте и в исполнительном элементе недопустимых перегрузок (механических, электрических и т. п.).
. Такое ограничение необходимо, например, в механических системах, когда регулируемой координатой является перемещение. Предупреждается появление в регулируемом объекте и в исполнительном элементе недопустимых перегрузок (механических, электрических и т. п.).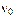 неизменяемой части системы меньше
неизменяемой части системы меньше 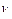 , то в усилительно-преобразовательном элементе необходимо иметь
, то в усилительно-преобразовательном элементе необходимо иметь 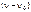 интегрирующих звеньев. Так же легко определяется необходимое значение передаточного коэффициента преобразовательно-усилительного элемента, равное
интегрирующих звеньев. Так же легко определяется необходимое значение передаточного коэффициента преобразовательно-усилительного элемента, равное 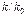 .
.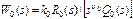 , (13.4)
, (13.4)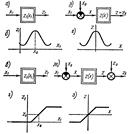 Нелинейные звенья можно классифицировать по различным признакам: симметрии (такую характеристику называют симметричной относительно оси ординат (рис.1 з, е) или четно-симметричной; симметричной относительно начала координат или нечетно-симметричной(рис.1 б, г).), гладкости (если в любой точке характеристики z (х) существует производная dz / dx, то характеристика относится к гладким. Если на характеристике имеются изломы, в которых производная dz / dx имеет разрыв, то характеристика относится к ломаным. Большую группу ломаных характеристик представляют кусочно-линейные характеристики, состоящие из отрезков прямых. В ряде случаев с целью облегчения расчета гладкие характеристики бывает удобно приближенно заменять кусочно-линейными ломаными.), однозначности (если каждому значению х соответствует одно определенное значение z, то характеристика однозначная. Если некоторому значению х соответствует несколько значений z в зависимости от режима, то характеристика многозначная, при этом число возможных значений z может лежать в пределах от 2 до ∞.), непрерывности характеристик (Если функция z (x) не имеет разрывов, то характеристику называют непрерывной. При наличии разрывов функции z (x) характеристику называют разрывной. Все рассмотренные примеры неоднозначных характеристик относятся к разрывным.).
Нелинейные звенья можно классифицировать по различным признакам: симметрии (такую характеристику называют симметричной относительно оси ординат (рис.1 з, е) или четно-симметричной; симметричной относительно начала координат или нечетно-симметричной(рис.1 б, г).), гладкости (если в любой точке характеристики z (х) существует производная dz / dx, то характеристика относится к гладким. Если на характеристике имеются изломы, в которых производная dz / dx имеет разрыв, то характеристика относится к ломаным. Большую группу ломаных характеристик представляют кусочно-линейные характеристики, состоящие из отрезков прямых. В ряде случаев с целью облегчения расчета гладкие характеристики бывает удобно приближенно заменять кусочно-линейными ломаными.), однозначности (если каждому значению х соответствует одно определенное значение z, то характеристика однозначная. Если некоторому значению х соответствует несколько значений z в зависимости от режима, то характеристика многозначная, при этом число возможных значений z может лежать в пределах от 2 до ∞.), непрерывности характеристик (Если функция z (x) не имеет разрывов, то характеристику называют непрерывной. При наличии разрывов функции z (x) характеристику называют разрывной. Все рассмотренные примеры неоднозначных характеристик относятся к разрывным.).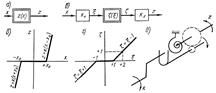
 контакты реле разомкнуты и о величине напряжения z, снимаемого с контакта реле, ничего сказать нельзя.
контакты реле разомкнуты и о величине напряжения z, снимаемого с контакта реле, ничего сказать нельзя.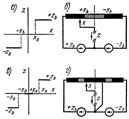 Звено типа «двухпозиционное реле с гистерезисом». Рассмотренные выше однозначные релейные характеристики соответствуют некоторой идеализации реальных систем. В действительности обычно величина входного сигнала, при котором происходит скачок выходной величины z, бывает различной для переключения контакта в прямом и обратном направлениях. Например, в двухпозиционном поляризованном реле при его симметричной регулировке переключение контакта в одном направлении происходит при некотором напряжении, а переключение в обратном направлении — при таком же напряжении противоположного знака.
Звено типа «двухпозиционное реле с гистерезисом». Рассмотренные выше однозначные релейные характеристики соответствуют некоторой идеализации реальных систем. В действительности обычно величина входного сигнала, при котором происходит скачок выходной величины z, бывает различной для переключения контакта в прямом и обратном направлениях. Например, в двухпозиционном поляризованном реле при его симметричной регулировке переключение контакта в одном направлении происходит при некотором напряжении, а переключение в обратном направлении — при таком же напряжении противоположного знака.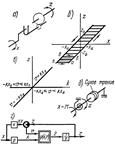 Звенья с многозначными характеристиками.
Звенья с многозначными характеристиками.


