Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание сау в частотной Области. Амплитудная и фазовая частотные характеристики сауСодержание книги
Поиск на нашем сайте
Частотные характеристики описывают передаточные свойства элементов и САУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а следовательно и реакции на них элемента или САУ могут быть представлены как сумма гармонических сигналов. В ТАУ наиболее часто используют следующие частотные характеристики: · амплитудная частотная характеристика (АЧХ); · фазовая частотная характеристика (ФЧХ); · амплитудно-фазовая частотная характеристика (АФЧХ). Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты
Рис. 2.13. Частотные характеристики: а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Пример ФЧХ приведен на рис. 2.13, б. Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменного j w: W(jw) = A(w) e jj (w) (показательная форма), (2.35) где A(w) – модуль функции; j (w) – аргумент функции. При изменении частоты от нуля до бесконечности вектор W(j w) поворачивается вокруг начала координат, при этом одновременно изменяется длина вектора. Кривая, которую при этом опишет конец вектора, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты Логарифмические частотные характеристики САУ При практических расчетах САУ (без применения электронных вычислительных машин) удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик. За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением частоты w i и его десятикратным значением 10 w i. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ) L(w) = 20 lg A(w), (2.41) ординаты которой измеряют в логарифмических единицах – беллах (Б) или децибеллах (дБ). Белл – единица измерения мощностей двух сигналов. Типовые звенья САУ Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев. Типовые динамические звенья являются основными составными частями алгоритмических схем непрерывных САУ, поэтому знание их характеристик существенно облегчает анализ таких систем. Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения
Инерционное 1-го порядка (апериодическое)
Инерционное 2-го порядка (апериодическое)
T1 ³ 2 T2 Инерционное 2-го порядка (колебательное)
T1 < 2 T2 Идеальное интегрирующее
Идеальное дифференцирующее
Реальное дифференцирующее
Звено запаздывания
Типовые звенья ТАУ 1. К - Усилительное звено. 2. p - Дифференцирующее звено. 3. 1/p - Интегрирующее звено (интегратор). 4. K/(Tp+1) - Инерционное (апериодическое) звено. 5. K/(T2p+2dTp+1) - Колебательное звено. 6. K(Tp+1) - Форсирующее звено. 7. K(T2p+2dTp+1) - Форсирующее звено 2-го порядка.
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.100 (0.006 с.) |

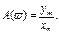 (2.34)
(2.34)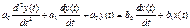 . (3.1) Безинерционное (пропорциональное)
. (3.1) Безинерционное (пропорциональное) 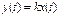 -
- 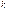
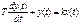 -
- 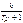
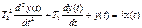 -
- 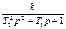
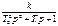
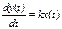 -
- 
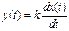 -
- 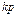
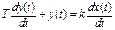 -
- 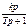
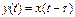 -
-