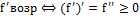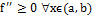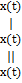Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки монотонности функции. Экстремумы функции и их признаки.Содержание книги
Поиск на нашем сайте
⊐ f определа на f имеет в т.
1) т.Ферма ↝ необходимый признак экстремума если 2) достаточные точки экстремума Признак 1. ⊐ f непрерывна на $ U( Если при пререходе через т. + → ‑ ↝ т. - → + ↝ т.
Замечание: f имеет непрерывную
Признак2: ⊐ дифференциал в некоторой окрестности точки если Доказательство: ⊐ ↝ в некоторой окрестности точки ↝ если хϵ этой окрестности и х< рисунок↝ Признаки монотонности: ⊐ f определена на Теорема 1. ⊐ f непрерывна на ⇐ ⊐ Замечание:1)f непрерывна 2)если f строго возрастает, то не обязательно f(x)= Теорема 2. f непрерына
Формула Тейлора и её применение к отысканию экстремума. f опр <a,b>; ↝f(x)-f(
При x 1) ⊐ n-четное ↝ если если 2) ⊐ n-нечет ↝ f'( n-нечет если n-нечет в f(x)= f’(x)= f’’(x)= f’’’(x)= f’’’’(x)= 33. Формы Лагранжа для
Если Чем меньше величина |x-
Частым случаем этой формулы при n-0 является теорема Лагранжа: f(x)=f( Для доказательства формулы (1) рассмотрим вспомогательную функцию j(z)=f(x)- Отметим, что jэ(я)= Введем функцию y(z)= $ сϵ[ j(ч)=0, y(x)=0, y( получим
Выпуклые функции (разностное и дифференциальные условия). Лемма: ⊐
Док-во: 1) если х=a 2) ⊐ xϵ Замечание: т.к. a+b=1 ↝ a=1-b↝x=a
⊐ f непрерывна " f (a Замечание: f называется вогнутой на f вогнутая ⟺ в (*)справедливо ≥ Разностное условие выпуклости: f опр f выпуклая на Т.о. f выпуклая на
f выпуклая ⇔ (**) Теорема 1: ⊐ f непрерывна на эквивалентны: 1) f выпуклая на 2)
Теорема 2: ⊐ f непрерывна на эквивалентны: 1) f выпуклая на f выпуклая 2)
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.009 с.) |

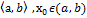
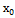 (локальный) max(min), если ∃ окрестность U=U(
(локальный) max(min), если ∃ окрестность U=U(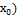 такое что f(
такое что f(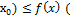 f(
f(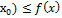 ) для xϵU
) для xϵU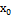 -т. экстремума (т.max или т.min)
-т. экстремума (т.max или т.min)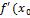 )=0, либо
)=0, либо 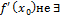
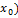 =U такое что дифференциал в U, за исключением может быть самой т.
=U такое что дифференциал в U, за исключением может быть самой т. 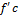 " сторонняя от
" сторонняя от 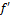 меняется знак
меняется знак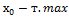
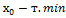
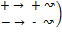 ↝ в
↝ в 
 знак
знак 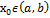 и ⊐
и ⊐ 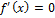 (т.е.
(т.е. 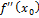
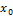 - точка min;
- точка min; 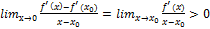
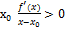
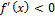 и х>
и х> 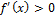
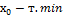
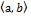 , f возрастает на
, f возрастает на 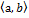 , если "
, если " 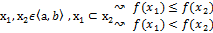 строго возрастает
строго возрастает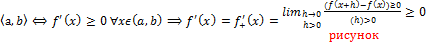
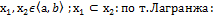 f(
f(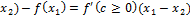 т.е. f(
т.е. f(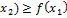
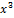 строго возрастает
строго возрастает 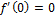
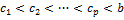
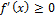 там где она $↝f возрастает на
там где она $↝f возрастает на 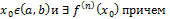 f’(
f’(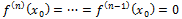
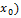 =
= 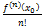 *
* 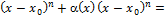
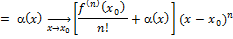
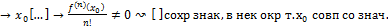
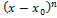 >0 при
>0 при 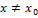

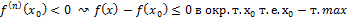
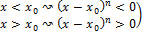 ↝f(x)-f(
↝f(x)-f(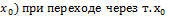 меняется знак↝ в
меняется знак↝ в 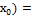 …=
…= 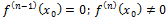
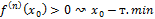 ,
, 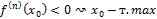
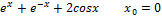
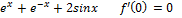
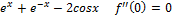
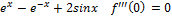
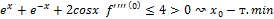
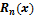 в формуле Тейлора.
в формуле Тейлора.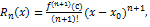 где с-нек.т, расположенная между x и
где с-нек.т, расположенная между x и 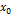
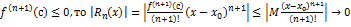 при n→∞
при n→∞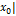 т ем быстрее
т ем быстрее  убывает с ростом n.
убывает с ростом n.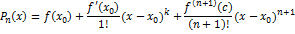
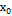 )+f’(c)*(x-
)+f’(c)*(x- 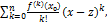 где zϵ[
где zϵ[ 

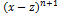 , где n+1>0
, где n+1>0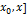 , что
, что 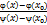 =
= 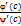 Учитывая, что
Учитывая, что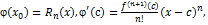
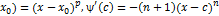
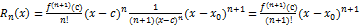
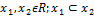
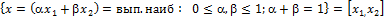
 xϵ
xϵ 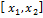
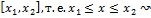
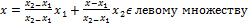
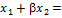 (1-b)
(1-b) 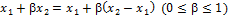 рисунок
рисунок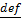 выпуклая на
выпуклая на  ϵ
ϵ 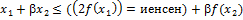 (*)
(*)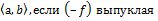
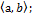 произв:
произв: 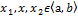 такое что
такое что 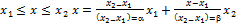
 )-f(x))⇔
)-f(x))⇔ 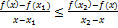 (**) рисунок
(**) рисунок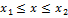 выполняется (**)
выполняется (**)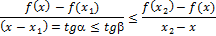
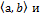 дифф-а в
дифф-а в 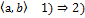
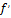 возрастает на
возрастает на 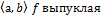 ↝выполнены разностные условие и
↝выполнены разностные условие и 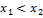
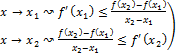 ↝
↝ 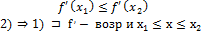
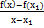 ≤
≤ 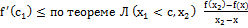 ≤
≤ 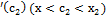 ↝
↝ 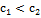 , то
, то 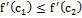 ⇔ разностное условие
⇔ разностное условие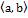 и в (a,b) $
и в (a,b) $ 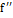 (x)
(x)