
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества и операции над ними. Их свойства.Стр 1 из 6Следующая ⇒
Вопросы для экзамена по математическому анализу. 1. Множества и операции над ними. Их свойства. 2. Определение функции. Образы и прообразы множеств. 3. Биекции, теорема о $ обратной функции. 4. Счетные множества и их свойства. 5. Множество 6. Определение о свойства 7. Предел монотонной последовательности. Число е. 8. Лемма о последовательности вложенных отрезков. Теорема об открытом покрытии отрезка. 9. Теорема Б-В о подпоследовательности. Критерий Б-К для сходимости числовой последовательности. 10. Множества мощности 11. Наибольший и наименьший пределы последовательности. 12. Определения придела функций на двух языках. 13. Свойства предела функции. 14. Односторонние пределы функции. 15. 16. Предел монотонной функции (один из вариантов). 17. Критерий Б-К для предела функции. 18. Определения непрерывности функции в точке. Непрерывность сужения и суперпозиции функций. 19. Теоремы Коши о непрерывной функции на промежутке. 20. Непрерывность монотоной функции. 21. Степень 22. Свойства показательной функции f(x)= 23. Логарифмическая функция и замечательные приделы 24. Теорема В о Наибольшем и наименьшем значениях Функции на отрезке. 25. Равномерная непрерывность функции на множестве. Теорема кантора о равномерной непрерывности функции. 26. Определение f'( 27. Дифференцируемые функции. Уравнение касательной прямой кграфику функции. 28. Производная суперпозиции функций. 29. Теорема Ферма, Ролля, Лагранжа и Коши. 30. Правила Лопиталя. 31. Признаки монотонности функции. Экстремумы функции и их признаки. 32. Формула Тейлора и её применение к отысканию экстремума. 33. Формы Лагранжа для 34. Выпуклые функции (разностное и дифференциальные условия).
Множества и операции над ними. Их свойства. · Способы задания: 1) перечисление (B= 2) описание (Х= · Операции: М – основное множество А,В с М 1) Объединение: А 2) Пересечение: А 3) Разность: А\В= · Свойства: 1) Дистрибутивные законы (А∪В)∩С=(А∩В) ∪ (В∩С), (А∩В) ∪С=(А∪С)∩(В∪С)
2) Законы двойственности (Де Морган)
Предел монотоной последовательности. Число е.
Теорема: - если - если Число Эйлера: e=2,718281828 конечный Определения придела функций на двух языках. I) Aϵ U(a),т.ч. f(U(a)∩X)ϵ ϑ(A) Станд.окр: 1)≠a,AϵR (конечные) lim f(x)=A↝для всех ε>0 $d≫0 для "xϵX x≠a, |x(x→a)-a|<d↝|f(x)-A|<e II) x≠∅ϵR; aϵ точки а (а-пред.т.мн-ва х, если для " U(a)↝ ϑ(a)∩X≠∅) 1)a-пред.т.Х, когда $
U(n)=(n;∞) a=+∞ Если а-пред.т. I эквивалетно II
Свойства предела функции x⊂ℝ; f,g 1) единственность: ⊐ 2) if 3) if 4) Аналогично:
5) предельный переход в нер-ве:
f(x)≤g(x) (xϵx, x≠a) 6) предел сужения: ⊐ ⊐ g= 7) предел суперпозиции: ⊐ h опр на
14. Односторонние пределы функции. x⊂ℝ; aϵ ℝ-пред.т.Х f:X→ ℝ
Определение: ⊐ а-пред.т Если $ аналог.прав.предел x=ℝ; f(x)=[x-цел.часть х]=E(x)-наиб.число, непровосх.Х Замечание: 1) если а-предел.т.Х, то она явл пред.т. хотя бы одного из множеств 2) если а явл. пред.т. только 3) если $ обыч. предел
1) $ 0<x<
разделим sinx на " вел.в неравенстве sinx<x<tgx 1>sinx/x>cosx ↝ 0<1 sinx/x<1-cosx=2 ↝ 2) следствие: 15.
Известно, что ↝ " п.посл { ⊐ { для " k найд.нат.число
положим ⊐
следствие 16. Предел монотонной функции (один из вариантов). ⊐ ф-я f опр на х⊂ℝ f убыв: " монотонной, если f-возр или f-убыв х⊂ℝ: f-монот на Х, а-пред.т.Х (аϵ Рисунок
Теор: $ f возраст на х⊂ℝ; а-пред.т.Х а=sup; (для I) a∉X тогда $ в частности: а) если f огр сверху, то f иеет в т. а кон lim, б) если f не огран сверху, то Док-во: (для кон а) a) ⊐ для "xϵX f(x)≤M<∞ тогда $ кон supf(x)=A
Докажем, что А= e>0↝$ x’ϵX, т.ч. А-e<f(x') ⊐ d=a-x’ (↝d>0) тогда если хϵХ и a-d<x<a↝A-e<f(x’)≤f(x)≤A a↝|f(x)-A|<e б) ⊐ supf(x)=∞ и число М∈ℝ $ x'ϵX,т.ч. M<f(x’) и ⊐ d=a-x’. Тогда "xϵX, т.ч. x’<x<a спр. M<f(x’)≤f(x) т.е. точно также аналогично можно с II,III,IV Определения непрерывности функции в точке. Непрерывность сужения и суперпозиции функций. Пусть функция f9x) определена в некоторой окрестности 0( Замечание: равенство (1) можно записать в виде: Пусть ∆x=x- Необходимое и достаточное условие непрерывности функции в точке. Функцияу=f(x) непрерывна в точке Замечание: условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны. пусть f(x) опр в полуинтервале [ Функция f(x) называется непрерывной справа в точке Пусть f(x) опрделена в полуинтервале ( Функция f(x) называется непрерывной слева в точке Теорема: (непрерывность сужения функции): Пусть f:X→ℝ; E⊂X; Если f непрерывна в точке (непрерывность суперпозиции функций) Пусть f:X→ℝ; g: X→ℝ; f(x)⊂Y: Тогда h=g◦f непрерывна в Пусть { т.к. f непр в т.к. g непр в Правила Лопиталя. Теорема 1: ⊐ функции f,g определены на (a,b>
3) 4) 5) $ Тогда $
Тогда f,g непрерывны на [a,b> и дифференциалы в (a,b) Рассмотрим a<x<b на [a,b] можем применить теорему Коши
Теорема 2: ⊐ f,g определены на <c,∞)
3) 4) 5) $ Тогда ⊐ ⊐ t= 1) 2)
3) 4) 5) Теорема 3: ⊐ f,g определена на (a,b> (-∞≤a)
3) 4) 5) $ Скорость стремления
2)
Вопросы для экзамена по математическому анализу. 1. Множества и операции над ними. Их свойства. 2. Определение функции. Образы и прообразы множеств. 3. Биекции, теорема о $ обратной функции. 4. Счетные множества и их свойства. 5. Множество 6. Определение о свойства 7. Предел монотонной последовательности. Число е. 8. Лемма о последовательности вложенных отрезков. Теорема об открытом покрытии отрезка. 9. Теорема Б-В о подпоследовательности. Критерий Б-К для сходимости числовой последовательности. 10. Множества мощности 11. Наибольший и наименьший пределы последовательности. 12. Определения придела функций на двух языках. 13. Свойства предела функции. 14. Односторонние пределы функции. 15. 16. Предел монотонной функции (один из вариантов). 17. Критерий Б-К для предела функции. 18. Определения непрерывности функции в точке. Непрерывность сужения и суперпозиции функций. 19. Теоремы Коши о непрерывной функции на промежутке. 20. Непрерывность монотоной функции.
21. Степень 22. Свойства показательной функции f(x)= 23. Логарифмическая функция и замечательные приделы 24. Теорема В о Наибольшем и наименьшем значениях Функции на отрезке. 25. Равномерная непрерывность функции на множестве. Теорема кантора о равномерной непрерывности функции. 26. Определение f'( 27. Дифференцируемые функции. Уравнение касательной прямой кграфику функции. 28. Производная суперпозиции функций. 29. Теорема Ферма, Ролля, Лагранжа и Коши. 30. Правила Лопиталя. 31. Признаки монотонности функции. Экстремумы функции и их признаки. 32. Формула Тейлора и её применение к отысканию экстремума. 33. Формы Лагранжа для 34. Выпуклые функции (разностное и дифференциальные условия).
Множества и операции над ними. Их свойства. · Способы задания: 1) перечисление (B= 2) описание (Х= · Операции: М – основное множество А,В с М 1) Объединение: А 2) Пересечение: А 3) Разность: А\В= · Свойства: 1) Дистрибутивные законы (А∪В)∩С=(А∩В) ∪ (В∩С), (А∩В) ∪С=(А∪С)∩(В∪С) 2) Законы двойственности (Де Морган)
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.77 (0.111 с.) |
 , сечения. Аксиома полноты и теорема о $ точных граней множества в
, сечения. Аксиома полноты и теорема о $ точных граней множества в 
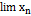 , неопределённости.
, неопределённости. и их свойства.
и их свойства.
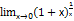
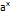 с вещественным показателем х.
с вещественным показателем х.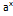
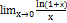 ,
,  ,
, 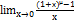
 , правила дифференцирования.
, правила дифференцирования. в формуле Тейлора.
в формуле Тейлора. f.e. B=
f.e. B= 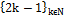 – нечётные числа)
– нечётные числа)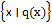 f.e. X=
f.e. X= 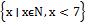 – ная числа меньше 7
– ная числа меньше 7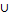 В =
В = 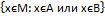 рисунок
рисунок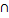 В=
В= 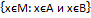
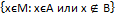
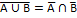 ,
, 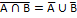
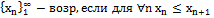
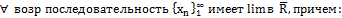
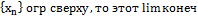
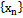 не огр, то lim=+∞
не огр, то lim=+∞
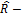 lim f при x→a,если ждя " ϑ(А) $ окрестность
lim f при x→a,если ждя " ϑ(А) $ окрестность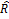 Если U(a)= ϑ(a)\{a}-пред.окр
Если U(a)= ϑ(a)\{a}-пред.окр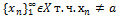

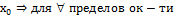 ϑ(ф)сод. беск.число т из х
ϑ(ф)сод. беск.число т из х : X→ ℝ; aϵ
: X→ ℝ; aϵ 
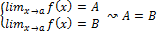
 ↝ $ U(a): if xϵ
↝ $ U(a): if xϵ 
 ↝ $ U(a): f огр в U(a)∩x
↝ $ U(a): f огр в U(a)∩x ↝ $
↝ $ 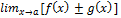 =A±B
=A±B
 (g(x)≠0, B≠0)
(g(x)≠0, B≠0) ↝A≤B
↝A≤B )
) если $
если $ 
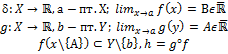
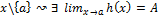 ↝
↝ 
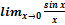
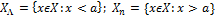
 ;
; 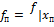 рисунок
рисунок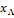
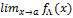 -то он называется левостор.предел f при x→a и обозн. через
-то он называется левостор.предел f при x→a и обозн. через 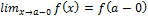
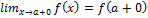

 ), то $-е f(a-0)⇔
), то $-е f(a-0)⇔ 
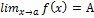 и а-пред.т.
и а-пред.т. 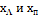 ,то $ f(a-0), f(a+0) f(a-0)=f(a+0)=
,то $ f(a-0), f(a+0) f(a-0)=f(a+0)= 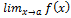
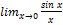 =1
=1 рисунок
рисунок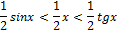
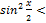 2sin
2sin  <2*x/2=x
<2*x/2=x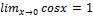
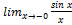 =
=  =
=  =1
=1 =1/2
=1/2  =1
=1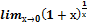
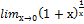 =e
=e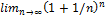 =e nϵℕ
=e nϵℕ нат.чисел,
нат.чисел, 

 т.ч.
т.ч. ↝
↝  т.о. доказано
т.о. доказано 
 =
= 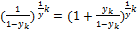 =
= 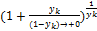 =
= 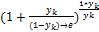 =
= 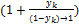
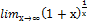 =
=  =e
=e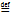 возраст: "
возраст: " 
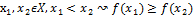
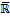 )
)
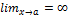
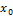 ) точки
) точки 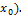

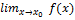 , равный значению функции f(x) в этой точке:
, равный значению функции f(x) в этой точке: 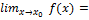 f(
f(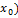
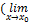 x), т.е. под знаком непрерывной функции можно переходить к пределу.
x), т.е. под знаком непрерывной функции можно переходить к пределу.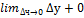
 .
.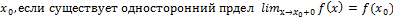
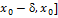

 существует односторонний предел
существует односторонний предел 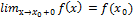
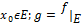
 f непрерывна в
f непрерывна в 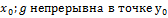
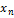
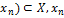 →
→ 
 , то g
, то g  =
= 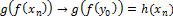
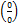 ®расрытие неопределенностей x®
®расрытие неопределенностей x® 
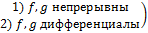 на (a,b>
на (a,b>

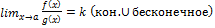

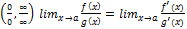 если правда lim $, то определим f,g в т. а положив f(a)=g(a)=0
если правда lim $, то определим f,g в т. а положив f(a)=g(a)=0 a<x<b®
a<x<b® 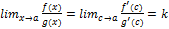

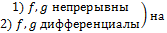 <c,∞)
<c,∞)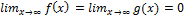

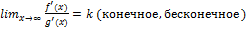
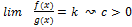

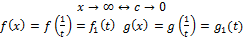
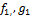 непрерывны на
непрерывны на 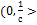 как суперпозиция непрерывных функций
как суперпозиция непрерывных функций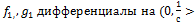
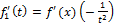
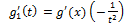

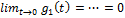

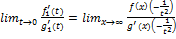 =k по т.1 ⊐
=k по т.1 ⊐ 
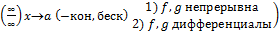 на (a,b>
на (a,b>
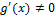

 рисунок
рисунок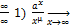 + ∞
+ ∞ 
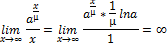

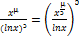
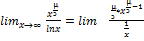 =
= 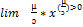 = + ∞
= + ∞


