Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность монотонной функции.
Признак непр (теорема 1): ⊐ монотонность на промежутке <a,b> и Y=f(<a,b>) тоже промежуток Тогда f непр на <a,b> Док-во: (от противного) ⊐ f возр на <a,b> и разрыв в f( Возьмем $ чиcло с т.ч. f(( По теореме о промеж знач: $ Если т.е. f( Сущ. непр.обратной функции к строго монотонной ⊐ f сторого монотонна и непр на <a,b> (по Т.о. мн-ве знач f(<a,b>)-промежуток) Тогда $ обр.ф. Итак, эта функция-биекция и следовательно $ Строгая монотонность Итак, Следствие: существование и непрерывность корня nϵM [0;∞) f(x)=
21. Степень f(x)= I. Степень с рац показ степени ⊐ fϵℚ; r=m\n (mϵZ,nϵM(N))
свойства: 1) 2) если a>1,то 3) 4) II) Лемма (дополнение к аксиоме полноты) ⊐ ∅≠A,B<R и 1) A≤B ("aϵA, "bϵB ↝a≤b) 2) "e>0 $ aϵA, bϵB, т.е. b-a<e 3)Тогда $ еденичный sϵR,т.ч. A≤s≤B Док-во: $ s' т.ч. A≤s’≤B и s’≠s Например: если aϵA; bϵB ↝ a≤s<s’≤b↝s’>s b-a≥s’-s>0 рисунок III) ⊐ a>1; xϵR- проивольная Положим A,B-удовлетворяет условиям Леммы ⇒A,Bϵ∅ 1) Если 2)⊐ e>0 0≤ Возьмем рацион
В следствие Леммы $ единств y, который развивает A и B Определение: Т.о. (a<1) 1) Если x=p рациональное (=m/n), то старое опредление совпадает с новым новое= 2) f.e. Но! r+p≤x+y≤r’+p’ ↝
Опрделение: Если 0<a<1,то 22. Свойства показательной функции f (x)= ⊐ a≠1 a>0 f(x)= Теорема: показ.ф-я f непрерывна на всей числовой оси (R) строго: Док-во: (для a>1): 1) строго возр: ⊐ По определению степени и свойства степени с рац.показателем 2) Док-м, что мн-во значений У=f(R)=(0;∞) ⊐хϵR ↝ $ рац. r≤x, а тогда ⊐ yϵ(0,∞) т.е. 0<y<∞
$x: Непрерывность функции следует из признака непрерывности для монотонной функции.
23. Логарифмическая функция и замечательные приделы ⊐ число а>0, a≠1 Т.к. f(x)= Непрерывная и строгая монотонность И множество значений есть (-∞;∞) Замечательные пределы: III) IV)
V)
Теорема В о Наибольшем и наименьшем значениях Функции на отрезке. ⊐ f опр на xϵR Число M(m) назыв наиб (наим) значением f на x
Теорема: Если f непрерввна на [a;b], то она ограничена и среди ее значений, тк есть наиб(М) и наим(m) Док-во: 1) док.что f не огр сверху, а это: "нат n, $ Теорема Б-В: $ подпосл.
f( Но f( 2) $ наиб.знач 1.$ конеч по определению sup " натур. n $ подпосл. f( "k:M-
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.128.129 (0.013 с.) |
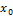 -т.разрыва
-т.разрыва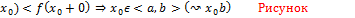
 f(
f(
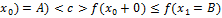

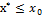 ↝ f(
↝ f( ≥inff(x)=f(
≥inff(x)=f(
 ,таким образом (m,M) ⊐
,таким образом (m,M) ⊐ :f(<a,b>)→<a,b> тоже строго монотонна (такого же типа, что и f) и непр на f(<a,b>) т.к. f строго монотонна, то f-инъекция, а если f рассмотреть как функцию f:<a,b>→f(<a,b>),то f-сюрьекция
:f(<a,b>)→<a,b> тоже строго монотонна (такого же типа, что и f) и непр на f(<a,b>) т.к. f строго монотонна, то f-инъекция, а если f рассмотреть как функцию f:<a,b>→f(<a,b>),то f-сюрьекция по Т1
по Т1  и множ.знач.=[0;∞)↝$
и множ.знач.=[0;∞)↝$ 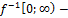 строго возр и непр на [0;∞)
строго возр и непр на [0;∞)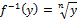
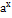 с вещественным показателем х.
с вещественным показателем х.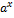 a>0 a≠1
a>0 a≠1
 зависима от представления r в виде дроби
зависима от представления r в виде дроби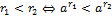

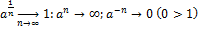
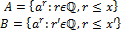
 , т.е. A<B
, т.е. A<B и
и 

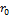 ≥x и натур n
≥x и натур n Тогда если
Тогда если 


 sup
sup  =inf
=inf 
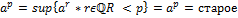
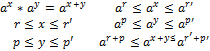


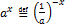
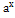
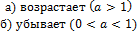 и множ.ее значений У=f(R) есть промеж (0;∞)
и множ.ее значений У=f(R) есть промеж (0;∞)

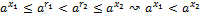

 ϵ
ϵ 

 r≤r’5
r≤r’5
 ,
,  ,
, 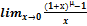
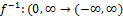
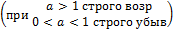

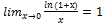 Известно, что
Известно, что  т.е.
т.е. 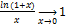
 =1
=1 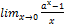 =lna
=lna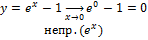
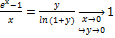
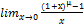 =µ
=µ 
 (непр.на (0,∞) как суперпозиция непр.функции
(непр.на (0,∞) как суперпозиция непр.функции

 :
:




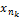 ®сϵ[a,b]
®сϵ[a,b]