Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение изображений тел, вписанных в призму
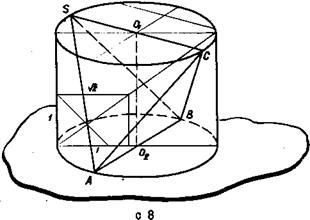
Обшее замечание. При построении изображений комбинаций многогранников и круглых тел мы не всегда будем различать задачи на вписывание и задачи на описывание. Основной принцип выбора – простота построения изображения. Поэтому иногда задачу на вписывание мы будем заменять задачей на описывание и наоборот. Задача 23. Построить изображение цилиндра, вписанного в прямую призму. Задачу на вписывание цилиндра в призму заменим задачей на описывание призмы около цилиндра. Решение этой задачи сводится к построению изображения основания цилиндра и описывания около него основания призмы. На рис.61 построено изображение цилиндра, вписанного в прямую призму, основанием которой является ромб.
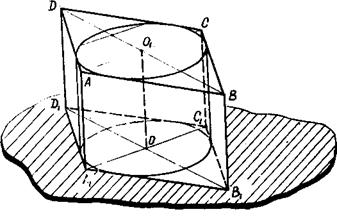
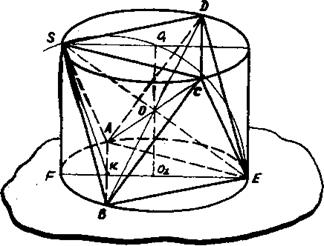
Задача 24. Построить изображение шара, вписанного в прямую призму. Решение задачи сводится к построению изображения многоугольника основания призмы, описанного около экватора шара. На рис.62 отражена последовательность построения изображения прямой призмы, описанной около шара. В основании призмы лежит ромбоид. (Ромбоидом называется четырехугольник, диагонали которого перпендикулярны и одна из них делит другую пополам).
Рис.62 Последовательность построений: 1) строим изображение шара и его экватора; 2) около экватора описываем ромбоид (на рис.62 в дан чертеж ромбоида, описанного около окружности): а) строим пару сопряженных прямых А2С2 и MN; б) через произвольную точку К диаметра экватора проводим B2D2║ MN; 3) строим изображение призмы: а) через вершины ромбоида проводим прямые, параллельные оси шара PQ; б) на построенных прямых откладываем отрезки A2A = A2A1 = B2B = B2B1=…= D2D = D2D1=
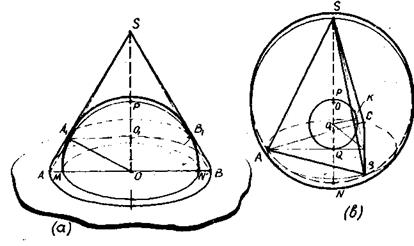
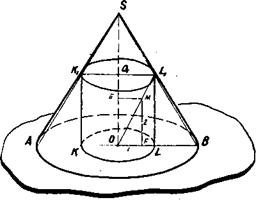
§ 15 Построение изображения тел, вписанных в пирамиду Задача 25. Построить изображение цилиндра, вписанного в пирамиду. Указание. При изображении цилиндра, вписанного в пирамиду, построение чертежа целесообразно начать с построения цилиндра. На рис.63 построено изображение цилиндра, вписанного в правильную треугольную пирамиду.
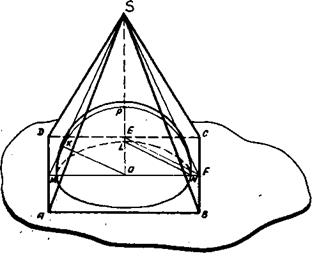
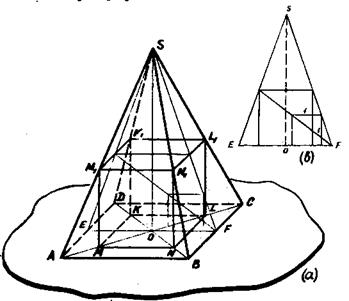
Изображение выполнено в следующей последовательности (рис.63, а). 1) строим изображение цилиндра; проводим высоту пирамиды OS; S – вершина пирамиды; 2) строим изображение правильного треугольника, описанного около верхнего основания цилиндра (∆ A1B1C1); 3) через центр нижнего основания цилиндра проводим ОA║O1A1 до пересечения с SA 1; 4) достраиваем пирамиду: проводим прямые SB 1 до пересечения с АВ (АВ║A1B1) и SC1 до пересечения с ВС (ВС║В1С1), строим АС. На рис.63,в дано упрощенное решение задачи 25 в «прямой» проекции. Задача 26. Построить изображение шара, вписанного в пирамиду. Построение изображения шара, вписанного в пирамиду, заменяют построением изображения пирамиды, описанной около шара. Это построение основано на пятой основной задаче (см.стр.39). Пример. Построить изображение шара, вписанного в пирамиду. В основании пирамиды трапеция, боковые ребра пирамиды наклонены к плоскости основания под равными углами (рис.64). Последовательность построений: I) строим изображение шар а и параллели шара (для наглядности параллельное сечение шара проводим черев точку О 1, взятую на оси шара так, чтобы
00 1: 0 1 P Рис.64 2) строим изображение трапеции (подобной трапеции основания пирамиды), описанной около параллели; 3) находим вершину пирамиды (см.пятую основную задачу, стр. 39); 4) строим одну из вершин основания пирамиды: проводим SA 1 и QА ║O1A1, находим точку А(А= QА х SA1); 5) строим пирамиду.
§ 16. Построение чертежей и задачам
При выполнении чертежей к задачам сочетание требований простоты и достаточной наглядности изображения имеет большое значение. Чтобы добиться сочетания этих требований, мы рекомендуем придерживаться следующих правил. Правило I. Приступая к решению задачи, нужно в первую очередь подумать о построении чертежа. С этой целью полезно провести анализ условия задачи: как можно подробнее выявить свойства фигур, подлежащих изображению; по возможности точнее определить их вид, взаимное расположение, представить необходимые (или возможные) дополнительные построения.
Правило 2. При построении чертежа нужно стараться плоскость, в которой предполагается выполнять какие-либо построения, изображать без искажения. Приведем несколько примеров.
Рис.65 Задача 28. Боковое ребро правиль ной четырехугольной усеченной пирамиды равно l, оно наклонено к плоскости основания под углом
Рис.66
Задача 29. В правильной треугольной пирамиде провести сечение через одну из сторон основания перпендикулярно в противолежащему ребру. Определить площадь сечения, если сторона основания равна а и боковое ребро пирамиды составляет с плоскостью основания угол
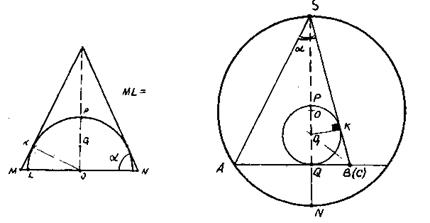
Указание. Так как плоскость SAD параллельна плоскости чертежа, то для построения сечения, перпендикулярного боковому ребру, можно сначала из точки D построить перпендикуляр DE к ребру AS. Правило 3. При решении задач на неправильные пирамиды, вершины которых проектируются в центр описанной около основания окружности, построение чертежа полезно начинать с изображения окружности и вписывания в нее основания пирамиды. Применение этого правила предполагает твердое знание следующей теоремы. Теорема. Если боковые ребра пирамиды равны между собой или наклонены к плоскости основания под равными углами, то высота пирамиды проходит через центр окружности, описанной около основания пирамида. Приведем примеры задач, при построении чертежей к которым целесообразно применить данное правило. Задача 30. Найти объем пирамиды, основанием которой служит прямоугольный треугольник с катетами а и в, если каждое боковое ребро ее наклонено к плоскости основания под углом Указание. Так как боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то вершина проектируется в центр описанной около основания окружности. Применяем правило. Изображаем окружность, вписываем прямоугольный треугольник ABC, проводим высоту S0, строим пирамиду.
 . Боковые ребра наклонены к плоскости основания под углом . Боковые ребра наклонены к плоскости основания под углом 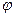 . Определить объем пирамиды (рис.69,в). . Определить объем пирамиды (рис.69,в).
Задача 32. В основании пирамиды лежит трапеция, у которой диагональ перпендикулярна к боковой стороне и образует с основанием угол
Все боковые ребра равны между собой. Боковая грань, проходящая через большее основание трапеции, имеет угол при вершине пирамиды
Рис.69 Заметим, что окружность, изображенная на чертеже, не является лишней. Она не только делает построения определенными, и тем самым помогает избежать ошибок при выполнении дополнительных построений, но делает чертеж более наглядным и нередко облегчает поиск пути решения задачи. Правило 4. При решении задач на неправильные пирамиды, вершины которых проектируется в центр вписанной в основание окружности, построение чертежа полезно начинать с изображения окружности и описывания около нее многоугольника основания пирамиды. Применение этого правила предполагает твердое знание следующей теоремы. Теорема. Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом или высоты боковых граней равны между собой, то высота пирамиды проходит через центр вписанного в основание круга. Приведем примеры задач на применение данного правила. Задача 33. Основанием пирамиды служит прямоугольный треугольник, гипотенуза которого с, а острый угол Задача 34. Основание пирамиды – равнобедренный треугольник, у которого угол между равными сторонами рами
Рис.70 Рис.71 Задача 35. Основанием четырехугольной пирамиды служит ромб, меньшая диагональ которого равна d, а острый угол
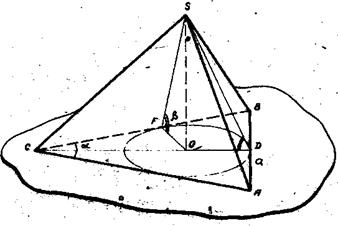
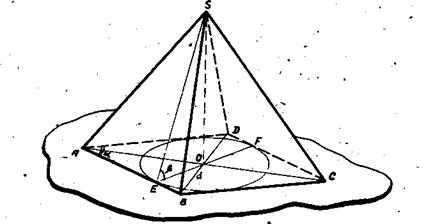
Правило 5. При вписывании шара в пирамиду, вершина которой проектируется в центр вписанной в основание окружности, целесообразно сначала в пирамиду вписать конус (около конуса описать пирамиду), ограничиваясь изображением основания конуса и образующей, проведенной в конец большой оси эллипса основания, а затем в конус вписать шар. Шар, вписанный в конус, одновременно будет вписан и в пирамиду. Задача 36. Ш ap вписан в пирамиду, в основании которой лежит равнобедренный треугольник с двумя равными углами
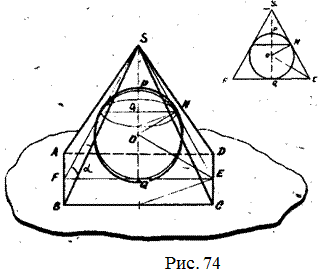
. Рис. 73
Задача 38. Основанием пирамиды служ ит ромб со стороной a и острым углом
Рис.75
Задача 39. B равносторонний конус вписан полушар так, что большой круг полушара находится в плоскости основания конуса. В каком отношении окружность касания делит боковую поверхность подушара и боковую поверхность конуса? [11,№ I9, стр.209], рис.76. Рис.76 Задача 40. В правильную четырехугольную пирамиду вписан полушар так, что его плоская грань параллельна основанию пирамиды, а шаровая поверхность касается его. Определить полную поверхность пирамиды, если боковые ее грани образуют с основанием угол Задача 41. В правильную четырехугольную пирамиду вписан полушар так, что плоская грань его лежит на основании пирамиды, а шаровая поверхность касается боковых граней пирамиды. Найти отношение полной поверхности полушара к полной поверхности пирамиды и объем полушара, если боковые грани наклонены к плоскости основания под углом
Рис.77
Рис.78 Рис.79
Задача 42. Сторона основания правильной треугольной пирамиды равна а, плоский угол при вершине равен Дополнение к правилу 6. При необходимости канонические проекции могут быть легко достроены до наглядного изображения, выполненного по правилам «прямой» проекции. Приведем иллюстрации к дополнению. Пусть к задаче 40 построена каноническая проекции (рис.80). По каким-то причинам нам захотелось получить более наглядное изображение. Используя «прямую» проекцию, поступим следующим образом (рис.80): а) построим изображение большого горизонтального круга полушара; б) проведем EF║LN и построим пирамиду (AD║SP; СD║NM); в) если нужно, построим контур шара.
Рис.80 Аналогичные дополнения можно сделать к каноническим изображениям, построенным к задачам 39, 42 (рис.81,а,в).
Рис.81 Правило 7. Если нужно построить чертеж к задаче с числовыми данными, то можно обобщить условие задачи: числовые данные, не оказывающие непосредственного влияния на геометрическую сторону задачи, заменить параметрами. Пусть нужно построить чертеж в следующей задаче. Основанием пирамиды служит ромб со стороной 20 см и острым углом 40°; двугранные углы при основании равны 60°. Определить радиус шара, вписанного в эту пирамиду. Чтобы построить чертеж, вместо числовых данных задачи (20 см, 40°, 60°) возьмем параметрические (например, а, В заключение руководства построим изображения в некоторым так называемым метрическим задачам. Чертежи выполнены по правилам «прямой» проекции или проекции близкой к кабинетной. Задача 43. В правильную четырехугольную пирамиду вписан куб так, что его четыре вершины находятся на боковых ребрах пирамиды, а остальные четыре – в плоскости ее основания. Определить ребро куба, если высота пирамиды равна Н. а боковое ребро равно l [1, № 693. стр.96], рис.82.
Задача 44. В правильную четырехугольную пирамиду вписан куб так, что вершины его лежат на апофемах пирамиды. Найти отношение объема пирамиды к объему куба, зная, что угол между высотой пирамиды и ее боковой гранью равен
Рис.83
Задача 45. В конус вписать равносторонний цилиндр (рис.84).
Рис. 84 Задача 46. В конус вписать куб (рис.85).
Рис.85 Задача 47. В цилиндр вписать правильный тетраэдр так, чтобы два противоположных ребра его являлись диаметрами оснований этого цилиндра (рис.86).
Рис.86 Задача 48. В цилиндр вписать правильный октаэдр так, чтобы две противоположные грани его были вписаны в основания цилиндра (рис.87). Задача 49. В шар вписать куб (рис.88)
Рис.87
Рис.88
Задача 50. В пирамиду, основанием которой служит равнобедренный треугольник, а боковое ребро, проходящее через вершины основания, перпеникулярно основанию, вписать шар (рис.89). Указания к некоторым задачам Задача 43. Чтобы найти положение верхней грана куба, нужно в треугольник вписать квадрат (рис.82,в). Применяем метод подобия. Задача 44. Чтобы найти положение верхней грани куба, нужно в треугольник SEF вписать прямоугольник с отношением сторон 1: Задача 47. Правильный тетраэдр можно вписать в цилиндр, если высота его так относится к диаметру основания, как 1: Задача 48. Построение чертежа полезно начинать с изображения основания цилиндра и вписывания в него правильного треугольника. Для дальнейших построений следует заметить, что КЕ = КS. Задача 49. Для нахождения положения оснований куба можно в изображение большого вертикального круга вписать прямоугольник с отношением сторон 1: Задача 50. Построение начинаем с изображения шара и проекции его на горизонтальную плоскость (плоскость основания пирамиды). Затем около пара описываем пирамиду.
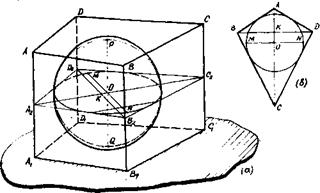
Дополнение В данном руководстве изображение шара выполнялось по правилам «прямой» проекции. Большинство же учебно-методических пособий для изображения шара рекомендует ортогональную проекцию. Поэтому мы сочли необходимым дать основные правила построения ортогональной проекции шара в дополнении, предоставляя самому читателю определить свои симпатии к той или иной проекции. Ортогональная проекция шара Задача 17. Построить изображение шара (см. задачу 17, стр. 36). Воспроизведем процесс ортогонального проектирования шара (рис.90).
Рис.90
Для получения ортогональной проекции расположим оригинал относительно плоскости проекции Р так, чтобы ось ого P 0 Q 0 была наклонена к плоскости Р и параллельна плоскости чертежа (классной доски).
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.248.208 (0.082 с.) |
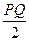 ; строим призму.
; строим призму.

 I:3); см.четвертую основную задачу;
I:3); см.четвертую основную задачу; Замечание. Если шар вписывается в усеченную пирамиду, то сначала его следует вписать в пирамиду, а затем построить верхнее основание усеченной пирамиды.
Замечание. Если шар вписывается в усеченную пирамиду, то сначала его следует вписать в пирамиду, а затем построить верхнее основание усеченной пирамиды.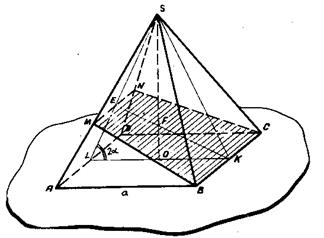 Задача 27. Построить сечение правильной четырехугольной пирамиды плоскостью, проходящей через сторону ее основания и делящей пополам двугранный угол при основании пирамиды. Определить площадь сечения, если сторона основания пирамиды равна а и двугранный угол при основании пирамиды равен 2
Задача 27. Построить сечение правильной четырехугольной пирамиды плоскостью, проходящей через сторону ее основания и делящей пополам двугранный угол при основании пирамиды. Определить площадь сечения, если сторона основания пирамиды равна а и двугранный угол при основании пирамиды равен 2  . Диагональ пирамиды перпендикулярна к боковому ребру ее. Определить объем пирамиды [1, № 690, стр.96], рис.66.
. Диагональ пирамиды перпендикулярна к боковому ребру ее. Определить объем пирамиды [1, № 690, стр.96], рис.66.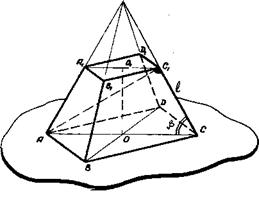
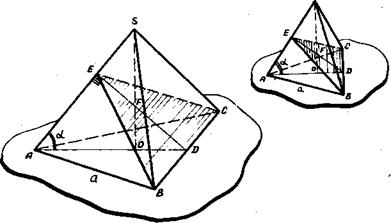
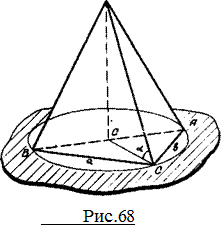
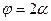 и площадь, равную S. Определить объем пирамиды и углы, под которыми наклонены грани к плоскости основания [ 1,№ 675,стр.93], рис.69,а.
и площадь, равную S. Определить объем пирамиды и углы, под которыми наклонены грани к плоскости основания [ 1,№ 675,стр.93], рис.69,а.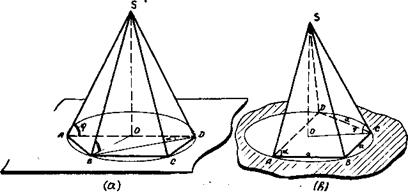
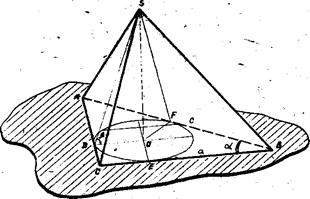

 Задача 37. В правильную четырехугольную пирамиду вписан шар. Расстояние центра шара от вершины пирамиды равно a, a угол наклона боковой грана ни пирамида к п лоскости основания равен
Задача 37. В правильную четырехугольную пирамиду вписан шар. Расстояние центра шара от вершины пирамиды равно a, a угол наклона боковой грана ни пирамида к п лоскости основания равен 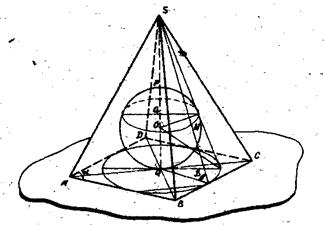
 Правило 6. При построении чертежей к задачам (особенно на комбинации с шаром) можно пользоваться или каноническими проекциями, или наглядными изображениями, дополненными выносными сечениями. Такие чертежи менее наглядны, но зато просты по исполнению.
Правило 6. При построении чертежей к задачам (особенно на комбинации с шаром) можно пользоваться или каноническими проекциями, или наглядными изображениями, дополненными выносными сечениями. Такие чертежи менее наглядны, но зато просты по исполнению.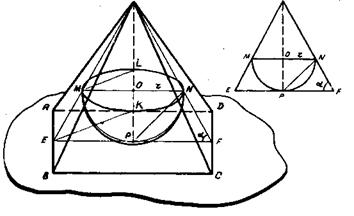
 )
)
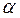 [1, № 694, стр.96],рис.83.
[1, № 694, стр.96],рис.83.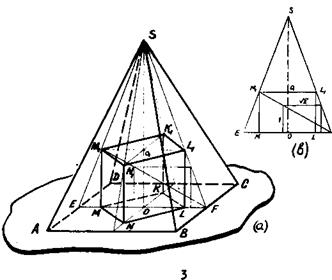


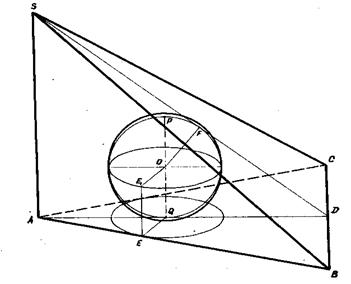
 (рис.83,в).
(рис.83,в).