Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полезно также применять цветные мелки.Стр 1 из 7Следующая ⇒
Предисловие
Краткое руководство к выполнению чертежей в стереометрии имеет целью систематизировать простейшие правила и приемы, дающие возможность достаточно быстро и просто делать «верные», наглядные чертежи. В руководстве не даются теоретические основы построения стереометрических чертежей, которые достаточно подробно изложены в ряде работ [3], [8], [11]. Оно имеет рецептурный характер и содержит лишь краткие сведения о проекциях, методические указания к выполнению чертежей и их образцы к некоторым наиболее характерным задачам, встречающимся в школьной практике. Предлагаемое руководство может служить методическим пособием для учителей математики при выполнении чертежей на доске; учащимся старших классов, оно окажется полезным при построении чертежей к задачам и теоремам стереометрии. Глава I ОБЩИЕ СВЕДЕНИЯ О ПЕДАГОГИЧЕСКОМ ЧЕРТЕЖЕ
§ 1. Параллельное проектирование
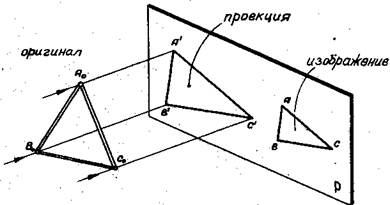
Свойства параллельных проекций Чертежи в стереометрии, как правило, выполняются по методу параллельных проекций. Сущность этого метода раскроется достаточно наглядно, если пространственную фигуру поместить перед какой-нибудь плоскостью Р в пучок параллельных лучей (рис.1).
Рис.1 «Тень», которая получится на плоскости Р, называется проекцией данной фигуры. Лучи, посредством которых получена проекция, называются проектирующими; плоскость Р – плоскостью проекций. В зависимости от направления проектирующих лучей различают два вида проекций: косоугольные и ортогональные. Проекция называется ортогональной, если она получена путем проектирования лучами, перпендикулярными плоскости проекций, и косоугольной, если проектирующие лучи наклонены к ней. Напомним основные свойства параллельных проекций. Свойство I. Проекция прямой есть прямая. Свойство 2. Проекции параллельных прямых параллельны. Свойство 3. Отношение проекций отрезков прямой (или отрезков, лежащих на параллельных прямых) равно отношению отрезков этой прямой (прямых). Свойство 4. Проекция фигуры, лежащей в плоскости, параллельной плоскости проекции, равна самой фигуре. Примечание. В частных случаях может случиться, что проекцией прямой будет точка (если направление прямой совпадет с направлением проектирования), проекцией параллельных прямых будет пара точек.
Из перечисленных свойств следует, что при параллельном проектировании почти всегда (за исключением частных случаев) сохраняются: а) прямолинейность прямых; б) параллельность прямых; в) отношение отрезков, лежащих на одной или на параллельных прямых. Следует также заметить, что при параллельном проектировании некоторые свойства фигур почти всегда меняются. Так, проекции равных отрезков, не лежащих на одной прямой или параллельных прямых, как правило, не являются равными, не равны в большинстве случаев и проекции равных углов.
§ 2. Основные требов ан ия к педагогическомучертежу
Свойства пространственных фигур можно изучать на моделях, но чаще всего пользуются изображениями этих фигур (например, на листе бумаги, в тетради, на доске). Под изображением (в отличие от проекции) понимают фигуру, подобную некоторой проекции данной фигуры (оригинала). Поясним это определение. Пусть нам дан равносторонний треугольник со стороной в 1 метр. Нужно построить его изображение. Сначала спроектируем данный треугольник на некоторую плоскость - получим проекцию треугольника. Если теперь построим фигуру, подобную проекции треугольника, то получим его изображение (рис.2).
Рис.2
В процессе преподавания стереометрии мы пользуемся именно изображениями фигур, а не их проекциями. П р и м е ч а н и е. Все элементы оригинала договоримся обозначать буквами с нуликом, а соответственные элементы изображения – теми же буквами без нулика. При изучении стереометрии роль изображений различна. В одних случаях изображение помогает создать представление об изучаемой фигуре, в других оно необходимо для выявления определенных свойств этой фигуры или помогает в решении задачи и т.д. В зависимости от назначения изображений различны требования, которые к ним предъявляются. Вместе с тем есть общие требования, которым должен удовлетворять всякий педагогический чертеж (чертеж, используемый в процессе обучения). Педагогический чертеж должен быть принципиально верным.
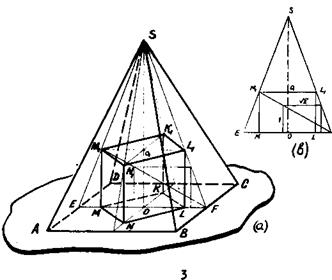
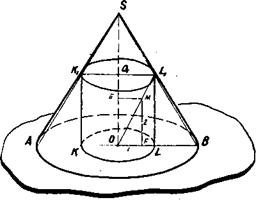
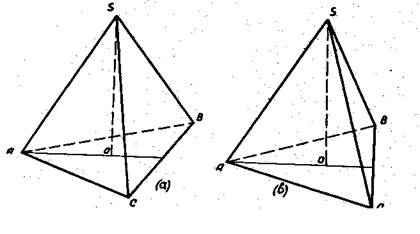
Это требование предельно четко: чертеж считается принципиально верным, если при его выполнении не нарушены основные свойства проекций, т.е. чертеж представляет собой изображение данной фигуры. Педагогический чертеж должен быть наглядным. Чертеж считается наглядным, если он дает достаточно четкое представление о форме оригинала. Требование наглядности относительно и субъективно. Наглядность зависит от развития пространственного воображения, и люди с разный запасом пространственных образов один и тот же чертеж могут воспринимать по-разному. Наглядность чертежа зависит от частоты употребления того или иного изображения. Так, например, чертеж правильной треугольной пирамиды при многократном изображении ее так, как показано на рис. 3, в, вызывает четкое представление об оригинале и не менее наглядное, чем на рис. 3,а. Большое значение для наглядности изображения имеет соблюдение основных правил оформления чертежей, независимо от того, выполняются ли они в тетради карандашом или на доске мелом, инструментами или от руки.
Рис.3 Перечислим наиболее важные правила оформления педагогического чертежа. 1. Чертеж должен быть крупным. Если чертеж сложный, скажем, содержит комбинации многогранников или многогранников и круглых тел, то в тетради (на доске) ему нужно отвести не менее четверти страницы (доски). 2. Необходимо соблюдать вид и толщину линий на чертеже: Таблица 1
Для получения на доске линий одинаковой толщины можно рекомендовать специальную заточку мела (рис.4).
Рис.4 3. Надписи на чертежах желательно выполнять шрифтом, близким к стандартному. 4. При изображении комбинаций тел (например, случаи вписывания) каждое из тел можно считать "прозрачным". Поэтому изображение вписанного тела выполняется в тех же видах линий, что и описанного. Лишь в целях наглядности толщину всех линий вписанного тела можно уменьшить в два раза по сравнению с толщиной линий описанного. Г л а в а II Изображение плоскостей
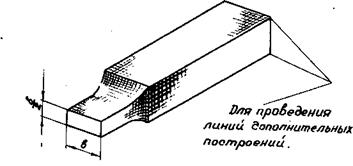
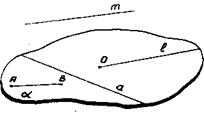
Условно плоскость на чертеже изображается или в виде параллелограмма, или в виде куска полосы, ограниченной с двух сторон параллельными прямыми, или в виде куска ее произвольной формы (рис.16). Плоскости будем обозначать малыми буквами греческого алфавита.
Рис.16 Прямая a0, лежащая в плоскости, изображается отрезком с концами на границе изображенного куска плоскости; луч l 0 с началом в точке О изображается отрезком с одним из концов на границе; отрезок АВ изображается отрезком, концы которого не принадлежат границе куска плоскости. Если прямая Изображения комбинаций прямых и плоскостей даны на рис.17. Рис.17 – чертеж к теореме о трех перпендикулярах; рис. 18 – чертеж к задаче №28, §1 из сб.задач Рыбкина (ч.П. Стереометрия); рис.19 -– чертеж к признаку параллельности двух плоскостей.
Рис.17 Рис.18
Рис.19 Следует обратить внимание, что при изображении плоскостей некоторые опорные линии на чертежах утолщены. Это сделано в целях получения большей наглядности изображения.
§ 5. Изображение многоугольников
Верность и наглядность изображений пространственных фигур во многом зависят от умения строить изображения их оснований. Поэтому целесообразно дать правила построения изображений многоугольников, наиболее часто встречающихся в школьной практике.
Задача I. Построить изображение правильного треугольника. Изображением правильного треугольника, вообще говоря, может служить треугольник произвольной формы. Однако, более привычно изображать правильный треугольник в проекции, близкой к кабинетной (рис.13,в). Задача 2. Построитьизображение квадрата. За изображение квадрата можно принять произвольный параллелограмм (рис.20,а), но более привычные изображения дает проекция, близкая к кабинетной (рис.20,в).
Рис.20 Последовательность построений: 1) строим отрезок АD (горизонтально); 2) строим АВ под углом близким к 45° к АD и АВ 3) достраиваем до параллелограмма. На рис.20,d дано изображение квадрата, но в другом положении: < ВОС ≈ 45°, ОВ ≈ ОD ≈
Задача 3. Построить изображение правильного пятиугольника.
Рис.21 При построении используем следующие свойства его сторон и диагоналей (рис.21,а): 1)В0D0 2)А0F0: F0С0 ≈ 3:2; D0 F0 : F0 В0≈ 3:2 Приближенное построение выполняется так (рис.21,в): 1) строим изображение равнобедренного треугольника А0С0Е0 – треугольник АСЕ; 2) делим сторону АС на пять равных частей и через точку F (AF: FC = 3:2) проводим В D 3) проводим АВ 4) точки D и С, В и С соединяем. Задача 4. Построить изображение правильного шестиугольника. Используем следующие свойства (рис.22,а): 1) F0B0 2) диагонали F0B0, F0C0 и центр правильного шестиугольника (точка О0) делят диагональ А0 D 0 на четыре равных отрезка (А0P0 = P0O0 = O0 L0 =L0 D0). Последовательность построений (рис.22,в): 1) горизонтальный отрезок А D делим на 4 равные части; 2) через точки P и Lпод углом, близким к 45° к А D, проводим прямые и на них откладываем равные отрезки PF = PB = LE = LC ≈
Рис.22 ABCDEF – изображение правильного шестиугольника.
Иногда целесообразно использовать изображение, данное на рис.22,с. Для построения такого изображения нужно: 1) взять произвольный отрезов MN и построить его середину (точку 0); 2) через точки M, N и 0 провести прямые под углом, близким к 45°, на которых отложить отрезки AF = СD и ВE = 2 DC, причем BE ≈ МО.
§ 6. Построение изображения окружности
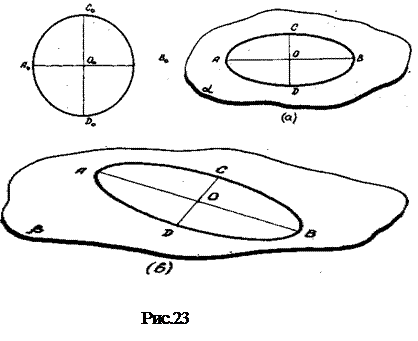
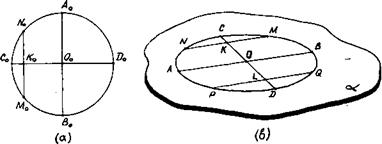
Известно, что проекцией окружности, вообще говоря, является эллипс (рис.23). Проекция центра окружности (точка 0) называется центром эллипса. Отрезок, соединяющий две точки эллипса, называется хордой; хорда, проходящая через центр эллипса, называется диаметром.
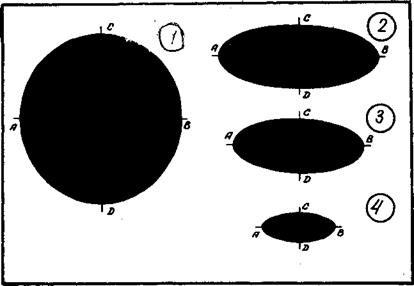
Диаметры эллипса, являющиеся проекциями двух взаимно перпендикулярных диаметров окружности, называются сопряженными. Эллипс имеет две оси симметрии (АВ и СD), которые называются осями эллипса. Оси эллипса перпендикулярны. В зависимости от метода проектирования и расположения окружности относительно плоскости проекций можно получить различные по расположению осей эллипсы (рис.23). Изображение на рис.23,а является наиболее наглядным изображением окружности. Его можно получить, в частности, в прямой проекции, если проектируемую окружность расположить в горизонтальной плоскости. Точное построение эллипса рассматривается в курсах черчения и выполняется по точкам с помощью лекал (рис.24,в). Для построения изображения окружности от руки можно воспользоваться приемом вписывания эллипса в прямоугольник с примерным соотношением сторон 1:2,5 (рис.24,а).
Рис.24 Чтобы изображения окружностей на чертежа была аккуратными, целесообразно применять набор шаблонов эллипсов, сделанных как для работы в тетради, так и для работы на доске (демонстрационных). Шаблоны для работы в тетради желательно изготовить из куска тонкого плотного картона или целлулоида, вырезав в нем эллипсы (рис.25). Размеры куска картона 120 мм х 160 мм.
Рис.25 Размеры шаблонов для работы в тетради указаны в таблице 2. Таблица 2
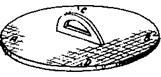
Демонстрационные шаблоны лучше делать вырезанными (рис.26). Размеры, данные в таблице, увеличить в 10 paз.
§ 7. Построение изображений многоугольников, вписанных в окружность
В основе построения изображений вписанных в окружность многоугольников лежит твердое знание решения следующей основной задачи. Первая основная задача. В окружности проведены два взаимно перпендикулярных диаметра. Построить изображение.
Рис.27 Решение. Обратимся к оригиналу (рис.27,а). Пусть A0B0
Отсюда вытекает последовательность построения изображения (рис.27,в): 1) строим изображение окружности (эллипс); 2) проводим две параллельные хорды (MN 3) строим изображение центра окружности – точку 0; 4) строим диаметр АВ На практике первая основная задача чаще встречается в более простом варианте. Задача. Дано изображение окружности с центром. Построить два сопряженных диаметра. Р е ш е н и е. Строим диаметр АВ я хорду К L, параллельную АВ (рис.28). Делим хорду К L пополам (точка Е – середина К L ). Через точки Е и 0 проводим диаметр С D. Диаметры АВ и С D – сопряженные (АВ и С D – изображение двух взаимно перпендикулярн ых диаметров окружности).
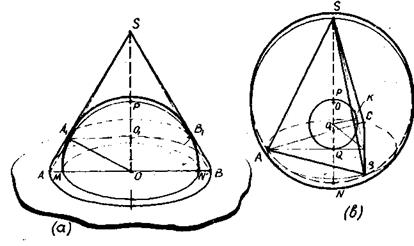
Рис.28 Глав а Ш Глава 1У Изображений комбинаций тел Третья основная задача. Построить сечение конуса плоскостью, параллельной плоскости основания. Р е ш е н и е (рис.49): 1) 2) строим В1С1 3) строим изображение сечения – эллипс с осями
Следует обратить внимание на тот факт, что концы большой оси эллипса сечения лежат на осевых образующих SA и SB, а сам эллипс касается контурных образующих. Решение этой задачи лежит в основе построения изображений цилиндра и призм, вписа нных в конус(см.стр. 41-42). Четвертая основная задача. Построить сечение шара плоскостью. параллельной плоскости экватора. Р е ш е н и е (рис.50): 1) строим изображение двух больших кругов шара (меридианный – круг, экваториальный – эллипс с осями АВ и СD): 2) проводим EF 3) строим изображение параллельного сечения – эллипс с осями EF и MN. Замечание. Необходимо следить, чтобы концы большой оси эллипса (точки Е и F), изображающего горизонтальное сечение шара, находились на большом меридианном круге, а сам эллипс выступал за изображение этого круга и касался контура шара.
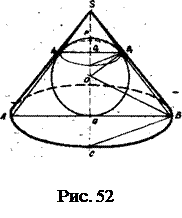
Рис.50 Рис.51 Четвертая основная задача обеспечивает построение изображений призм, пирамид, цилиндра и конуса, вписанных в шар (см. § 13). Пятая основная задача. Дано изображение шара и его параллели. На продолжении оси шара построить точку, все касательные из которой к шару касаются его поверхности в точках параллели. Р е ш е н и е (рис.51): 1) строим изображение шара и его горизонтального сечения (параллели); 2) 3) строим FS 4) находим искомую точку S (S =PQ х FS). Умение решать эту задачу позволяет достаточно просто строить изображения некоторых видов пирамид, описа нных около шара (см.стр.47). Шестая основная задача. Построить изображение шара, вписанного в конус. Решение (рис.52): 1) строим конус и осевое сечение SАВ; 2) в осевое сечение вписываем окружность – изображение большого меридианного круга шара; 3) строим изображение окружности касания поверхности конуса с поверхностью шара: а) из центра шара опускаем перпендикуляр ОB1 на SB; б) проводим A1B1 в) через точку O 1(O1=SO x A 1B1) строим горизонтальное сечение конуса – эллипс, который и будет изображением искомой окружности; 4) строим контур шара. Замечания: а) при построении чертежей к задачам контур шара можно не строить; б) следует следить, чтобы большой меридианный круг шара был вписан в осевое сечение конуса, но не касался его контурных образующих, а контур шара обязательно касался контурных образующих конуса; в) контур шара должен пересекать диаметр АВ основания конуса. Шестая основная задача будет нами широко применяться при построении изображений к задачам на вписывание шара в пирамиды (см. стр.53).
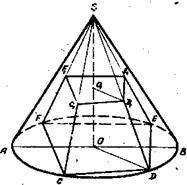
§ 12. Построение изображений тел, вписанных в конус Задача 18. Построить изображение пирамиды, вписанной в конус. Решение задачи сводится к вписыванию многоугольника основания пирамиды в основание конуса. На рас.53 дано изображение правильной треугольной пирамиды, вписанной в конус. Замечания: а) один из сопряженных диаметров (на рисунке диаметр МА) рекомендуется в большинстве случаев брать близким к горизонтальному; в этом случае ребро SC не будет закрываться высотой конуса;
б) изображение, данное на рис.53, в, полезно выполнять при построении чертежей к задачам.
Задача 19. Построить изображение усеченной пирамиды, вписанной в конус. При построении изображения усеченной пирамиды, вписанной в конус, сначала вписывают полную пирамиду, а затем строят сечение пирамиды плоскостью, параллельной плоскости основания конуса. На рис.54 построено изображение усеченной четырехугольной пирамиды, вписанной в конус.
Рис.54
Задача 20. Построить изображение прямой призмы, вписанной в конус. В основании призмы лежит прямоугольный треугольник. Замечание. Построение изображений призмы или цилиндра, вписанных в конус, основано на умении решать третью основную задачу (см.стр.38). Последовательность построений (рис.55,а): 1) строим изображение конуса и сечения его плоскостью, параллельной плоскости основания; 2) в сечение конуса вписываем верхнее основание призмы; 3) через вершины верхнего основания проводим прямые, параллельные высоте конуса, и откладываем на них отрезки, равные высоте призмы (N1N = M1M = P1P = O1O); 4) строим нижнее основание призмы.
Рис.55 Последовательность построений: строим верхнее основание призмы; проводим образующу SL (SL проходит через вершину А); строим L0; строим вершину A1 (A1 = A1A x OL; A 1A Р
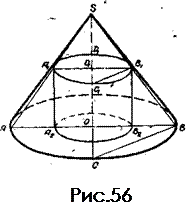
§13. Построение изображений тел, вписанных в шар
Задача 21. Построить изображение конуса, вписанного в шар. Решение задачи (рис.57) сводится к построению параллели ша ра (см.стр. 38). Задача 22. Построить изображение пирамиды, вписанной в шар. Решение задачи сводятся к вписыванию основания пирамиды в окружность горизонтального сечения шара.
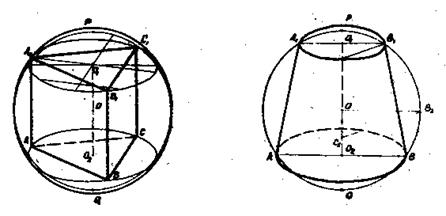
Замечания: а) для построения изображений цилиндра или прямой призмы, вписанных в шар, строят изображения двух параллелей шара, расположенных на равных расстояниях по разные стороны от его центра; на рис.59 дано изображение прямой призмы, в основании которой равносторонний треугольник, вписанной в шар; б) на рис.60 построено изображение усеченного конуса, вписанного в шар
.
Рис.59 Рис.60
Рис.66
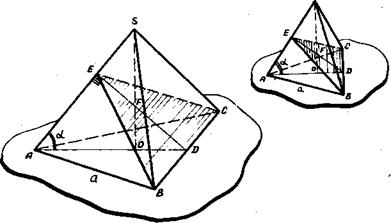
Задача 29. В правильной треугольной пирамиде провести сечение через одну из сторон основания перпендикулярно в противолежащему ребру. Определить площадь сечения, если сторона основания равна а и боковое ребро пирамиды составляет с плоскостью основания угол
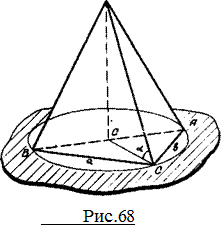
Указание. Так как плоскость SAD параллельна плоскости чертежа, то для построения сечения, перпендикулярного боковому ребру, можно сначала из точки D построить перпендикуляр DE к ребру AS. Правило 3. При решении задач на неправильные пирамиды, вершины которых проектируются в центр описанной около основания окружности, построение чертежа полезно начинать с изображения окружности и вписывания в нее основания пирамиды. Применение этого правила предполагает твердое знание следующей теоремы. Теорема. Если боковые ребра пирамиды равны между собой или наклонены к плоскости основания под равными углами, то высота пирамиды проходит через центр окружности, описанной около основания пирамида. Приведем примеры задач, при построении чертежей к которым целесообразно применить данное правило. Задача 30. Найти объем пирамиды, основанием которой служит прямоугольный треугольник с катетами а и в, если каждое боковое ребро ее наклонено к плоскости основания под углом Указание. Так как боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то вершина проектируется в центр описанной около основания окружности. Применяем правило. Изображаем окружность, вписываем прямоугольный треугольник ABC, проводим высоту S0, строим пирамиду.
 . Боковые ребра наклонены к плоскости основания под углом . Боковые ребра наклонены к плоскости основания под углом 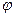 . Определить объем пирамиды (рис.69,в). . Определить объем пирамиды (рис.69,в).
Задача 32. В основании пирамиды лежит трапеция, у которой диагональ перпендикулярна к боковой стороне и образует с основанием угол
Все боковые ребра равны между собой. Боковая грань, проходящая через большее основание трапеции, имеет угол при вершине пирамиды
Рис.69 Заметим, что окружность, изображенная на чертеже, не является лишней. Она не только делает построения определенными, и тем самым помогает избежать ошибок при выполнении дополнительных построений, но делает чертеж более наглядным и нередко облегчает поиск пути решения задачи. Правило 4. При решении задач на неправильные пирамиды, вершины которых проектируется в центр вписанной в основание окружности, построение чертежа полезно начинать с изображения окружности и описывания около нее многоугольника основания пирамиды. Применение этого правила предполагает твердое знание следующей теоремы. Теорема. Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом или высоты боковых граней равны между собой, то высота пирамиды проходит через центр вписанного в основание круга. Приведем примеры задач на применение данного правила. Задача 33. Основанием пирамиды служит прямоугольный треугольник, гипотенуза которого с, а острый угол Задача 34. Основание пирамиды – равнобедренный треугольник, у которого угол между равными сторонами рами
Рис.70 Рис.71 Задача 35. Основанием четырехугольной пирамиды служит ромб, меньшая диагональ которого равна d, а острый угол
Правило 5. При вписывании шара в пирамиду, вершина которой проектируется в центр вписанной в основание окружности, целесообразно сначала в пирамиду вписать конус (около конуса описать пирамиду), ограничиваясь изображением основания конуса и образующей, проведенной в конец большой оси эллипса основания, а затем в конус вписать шар. Шар, вписанный в конус, одновременно будет вписан и в пирамиду. Задача 36. Ш ap вписан в пирамиду, в основании которой лежит равнобедренный треугольник с двумя равными углами . Рис. 73
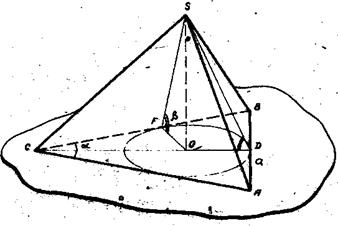
Задача 38. Основанием пирамиды служ ит ромб со стороной a и острым углом
Рис.75
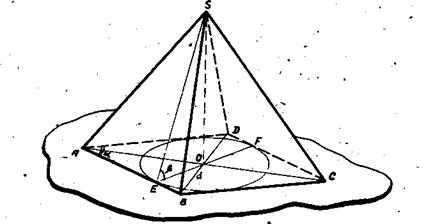
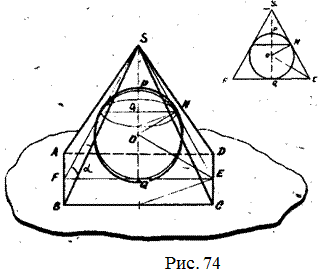
Задача 39. B равносторонний конус вписан полушар так, что большой круг полушара находится в плоскости основания конуса. В каком отношении окружность касания делит боковую поверхность подушара и боковую поверхность конуса? [11,№ I9, стр.209], рис.76. Рис.76 Задача 40. В правильную четырехугольную пирамиду вписан полушар так, что его плоская грань параллельна основанию пирамиды, а шаровая поверхность касается его. Определить полную поверхность пирамиды, если боковые ее грани образуют с основанием угол Задача 41. В правильную четырехугольную пирамиду вписан полушар так, что плоская грань его лежит на основании пирамиды, а шаровая поверхность касается боковых граней пирамиды. Найти отношение полной поверхности полушара к полной поверхности пирамиды и объем полушара, если боковые грани наклонены к плоскости основания под углом
Рис.77
Рис.78 Рис.79
Задача 42. Сторона основания правильной треугольной пирамиды равна а, плоский угол при вершине равен Дополнение к правилу 6. При необходимости канонические проекции могут быть легко достроены до наглядного изображения, выполненного по правилам «прямой» проекции. Приведем иллюстрации к дополнению. Пусть к задаче 40 построена каноническая проекции (рис.80). По каким-то причинам нам захотелось получить более наглядное изображение. Используя «прямую» проекцию, поступим следующим образом (рис.80): а) построим изображение большого горизонтального круга полушара; б) проведем EF║LN и построим пирамиду (AD║SP; СD║NM); в) если нужно, построим контур шара.
Рис.80 Аналогичные дополнения можно сделать к каноническим изображениям, построенным к задачам 39, 42 (рис.81,а,в).
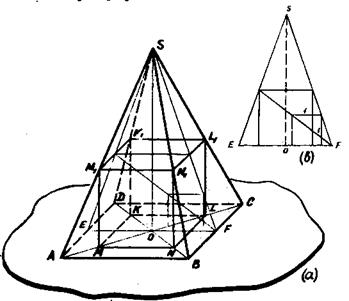
Рис.81 Правило 7. Если нужно построить чертеж к задаче с числовыми данными, то можно обобщить условие задачи: числовые данные, не оказывающие непосредственного влияния на геометрическую сторону задачи, заменить параметрами. Пусть нужно построить чертеж в следующей задаче. Основанием пирамиды служит ромб со стороной 20 см и острым углом 40°; двугранные углы при основании равны 60°. Определить радиус шара, вписанного в эту пирамиду. Чтобы построить чертеж, вместо числовых данных задачи (20 см, 40°, 60°) возьмем параметрические (например, а, В заключение руководства построим изображения в некоторым так называемым метрическим задачам. Чертежи выполнены по правилам «прямой» проекции или проекции близкой к кабинетной. Задача 43. В правильную четырехугольную пирамиду вписан куб так, что его четыре вершины находятся на боковых ребрах пирамиды, а остальные четыре – в плоскости ее основания. Определить ребро куба, если высота пирамиды равна Н. а боковое ребро равно l [1, № 693. стр.96], рис.82.
Задача 44. В правильную четырехугольную пирамиду вписан куб так, что вершины его лежат на апофемах пирамиды. Найти отношение объема пирамиды к объему куба, зная, что угол между высотой пирамиды и ее боковой гранью равен
Рис.83
Задача 45. В конус вписать равносторонний цилиндр (рис.84).
Рис. 84
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.66.55 (0.236 с.) |
 (6 - 8)
(6 - 8)
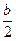
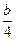 и менее
и менее
 (1 -1,5)
(1 -1,5)

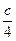 и менее
и менее
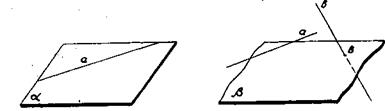
 не лежит в плоскости, то отрезок
не лежит в плоскости, то отрезок 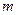 , изображающий прямую, не должен иметь общих точек с изображением плоскости или пересекать границу куска плоскости.
, изображающий прямую, не должен иметь общих точек с изображением плоскости или пересекать границу куска плоскости.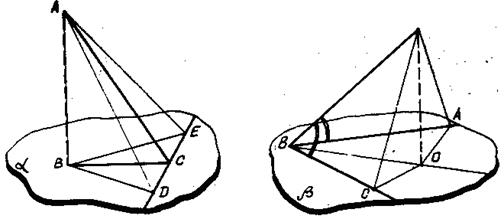
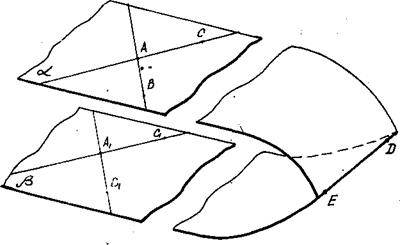



 АD;
АD;
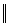 А0Е0; Е0 D0
А0Е0; Е0 D0  AD
AD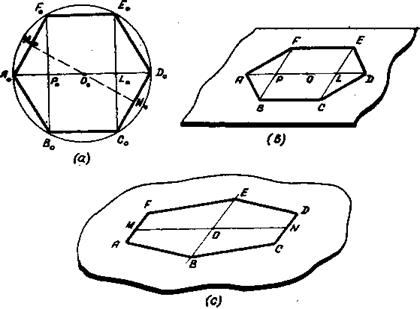

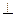 С0D 0. Если M0N0
С0D 0. Если M0N0 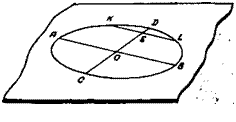 Покажем применение первой основной задачи к построению изображений многоугольников, вписанных в окружность
Покажем применение первой основной задачи к построению изображений многоугольников, вписанных в окружность через произвольную точку 01 высоты конуса проведен отрезок A 1B1 параллельно АВ;
через произвольную точку 01 высоты конуса проведен отрезок A 1B1 параллельно АВ;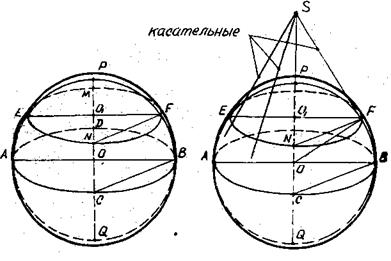
 проводим радиус OF в конец большой оси эллипса сечения;
проводим радиус OF в конец большой оси эллипса сечения;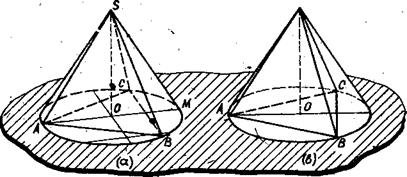
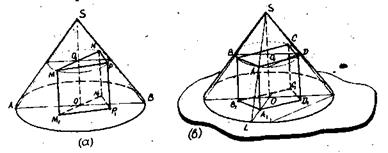
 Можно применить и иную последовательность построений изображения прямой призмы, вписанной в конус. На рис.55, в вписана призма, в основании которой лежит трапеция.
Можно применить и иную последовательность построений изображения прямой призмы, вписанной в конус. На рис.55, в вписана призма, в основании которой лежит трапеция.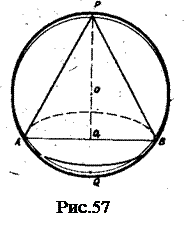 На рис.58,а дано изображение правильной треугольной пирамиды, вписанной в шар, а на рис.58, в – пирамиды с равными боковыми ребрами к основанием в форме трапеции.
На рис.58,а дано изображение правильной треугольной пирамиды, вписанной в шар, а на рис.58, в – пирамиды с равными боковыми ребрами к основанием в форме трапеции.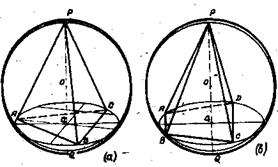
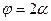 и площадь, равную S. Определить объем пирамиды и углы, под которыми наклонены грани к плоскости основания [ 1,№ 675,стр.93], рис.69,а.
и площадь, равную S. Определить объем пирамиды и углы, под которыми наклонены грани к плоскости основания [ 1,№ 675,стр.93], рис.69,а.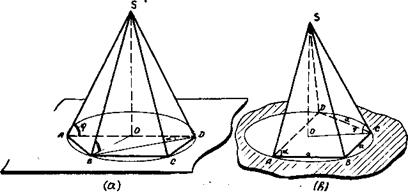
 . Определить полную поверхность [10, № 1750, стр.122], рис.70.
. Определить полную поверхность [10, № 1750, стр.122], рис.70.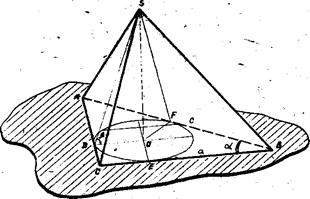

 Задача 37. В правильную четырехугольную пирамиду вписан шар. Расстояние центра шара от вершины пирамиды равно a, a угол наклона боковой грана ни пирамида к п лоскости основания равен
Задача 37. В правильную четырехугольную пирамиду вписан шар. Расстояние центра шара от вершины пирамиды равно a, a угол наклона боковой грана ни пирамида к п лоскости основания равен 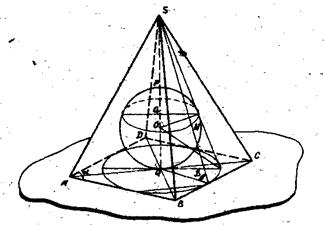
 Правило 6. При построении чертежей к задачам (особенно на комбинации с шаром) можно пользоваться или каноническими проекциями, или наглядными изображениями, дополненными выносными сечениями. Такие чертежи менее наглядны, но зато просты по исполнению.
Правило 6. При построении чертежей к задачам (особенно на комбинации с шаром) можно пользоваться или каноническими проекциями, или наглядными изображениями, дополненными выносными сечениями. Такие чертежи менее наглядны, но зато просты по исполнению.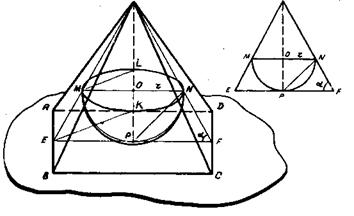
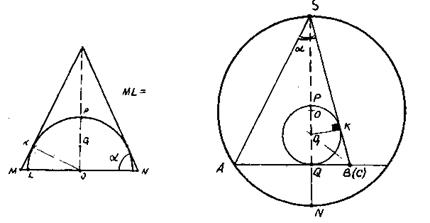
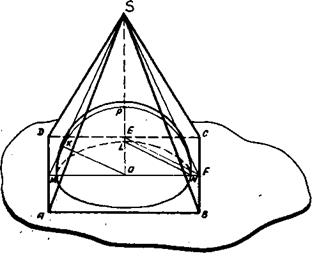
 )
)
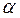 [1, № 694, стр.96],рис.83.
[1, № 694, стр.96],рис.83.